先进汽车缓速器理论与试验：热流场耦合计算成果

使用CFX得到定子的温度分布后，将定子冷却液管道壁面的传热系数作为边界条件施加在缓速器的永久磁铁数学模型上，即可计算缓速器中转子和永磁体的温度分布。计算模型中转子和定子间的气隙简化为1D薄壁热传导问题。该部分计算可以在Workbench中采用稳态热（Steady-state Thermal）分析进行计算。基本过程如下：

1）定义材料属性。可在Engineering Data中完成。

2）建立模型。同上述分析中建立模型类似，在DesignMolder中完成。由于是平面模型，因此绘制草图后生成Surface即可。

3）划分网格。设置网格大小后自动划分即可。

4）边界条件设置。分别设置壁面传热系数、生热率以及转子内表面温度（假设为40℃）。忽略热辐射及其他壁面的热损失。

图5-45 冷却液不同流量时永久磁铁的温度分布

5）后处理。求解后可观察永久磁铁的温度分布，如图5-45为冷却液不同流量时永久磁铁的温度分布。

永磁体高速旋转会加快气隙热量的传导，永磁体高速旋转时气隙等效导热系数与静态气隙导热系数之比的计算公式为(www.xing528.com)

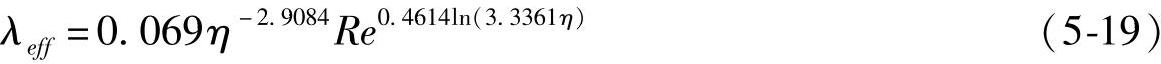
式中，η=r_o/R_i，r_o是转子外半径，单位为m；R_i是定子内半径，单位为m；雷诺数Re=r_oω_mδ/ν，ω_m是转子角速度，单位为rad/s，气隙高度δ=R_i-r_o，单位为m，ν为空气的运动粘度，单位为m²/s。气隙物理性质的定性温度可通过迭代计算确定。

在图5-46中展示了永磁体最高温度随冷却液流量变化的曲线，边界条件中的热源生热率为7.59E+08W/m³。与图5-41比较可知，两条曲线的变化趋势相似，而冷却液流量的变化对定子温度分布的影响比对永磁体温度分布的影响要更为显著，图5-41中最大温度与最小温度的温度差约200K，而图5-46中只有约10K，气隙热阻较大是这一现象的原因之一。此外，忽略了热辐射及计算模型的简化也会产生计算误差。

随汽车行驶路况的不同，需要提供不同的制动功率。因此，在图5-47中展示了永磁体最高温度随制动功率变化的曲线。由图5-47可见，永磁体最高温度是随制动功率线性变化的。

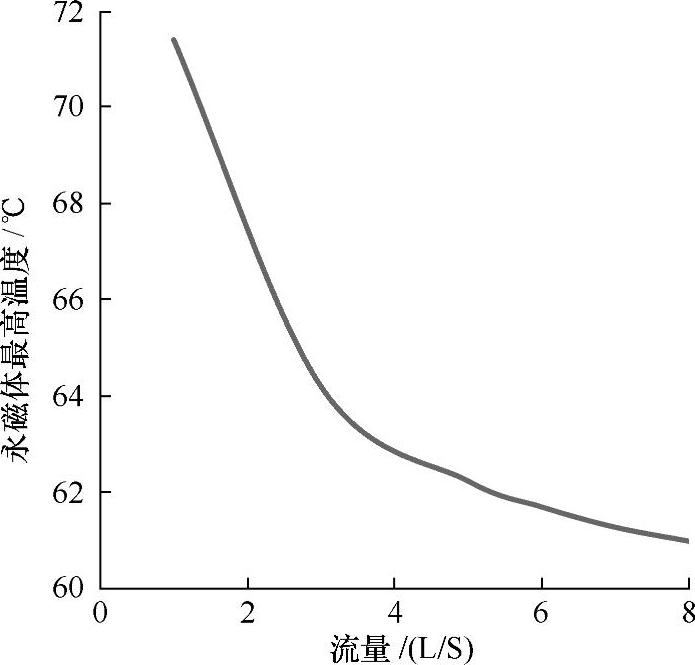
图5-46 永磁体最高温度随冷却液流量变化的曲线

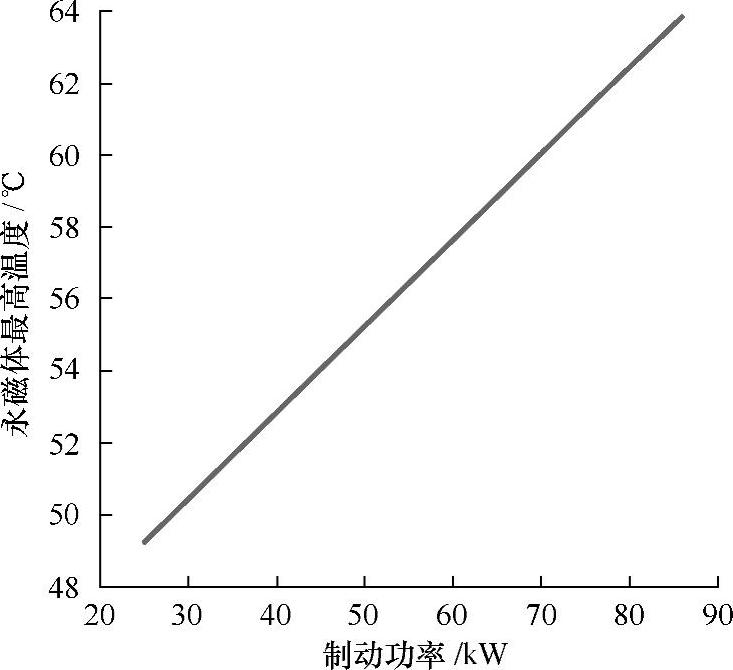
图5-47 永磁体最高温度随制动功率变化的曲线