瞬态缓速器电磁场计算及试验结果

图5-12给出了缓速器在1000r/min时不同计算时间下的2D磁通分布。为更清楚地表达瞬态磁通的变化，设缓速器转子相对静止，定子相对转子逆时针运动，并定义永磁体宽度方向的两边为∑输入边”和∑输出边”，相对于定子的周向运动来说，它们分别对应永磁体的∑前边”和∑后边”，如图5-12a所示。这样当定子经过每个永磁体的前边时，定子上每个点从永磁体的输入边运动到输出边。当t=0s时，转子处于静止状态，永磁体两边对应磁通和磁力线分布是一样的。当t=0.005s时，磁通开始在靠近输出边一侧变强，而靠近输入边一侧变弱，这与电磁场数学模型中涡流磁动势分析是一致的。当t从0.005s到0.02s时，气隙磁通不断被涡流磁动势减弱，从而涡流也变小，最终气隙磁通达到平衡。因此，在每一个永磁体对应的定子范围内，总是有一半的气隙磁通密度被加强，而另一边被减弱。但由于定子材料存在非线性磁饱和特性，总的气隙磁通密度是减少的。

图5-13给出了不同转速时永磁缓速器3D模型的气隙磁通密度分布。与电机中的电枢反应一样，气隙磁通密度一边减少，一边略有增加。随着转速的升高，由于涡流增大，涡流磁动势增大，导致气隙磁通密度减小部分更明显。转速增大，使得气隙平均磁通密度不断减小，从而使涡流感应的磁通密度减小，最后缓速器的制动力矩也达到饱和值。

永磁缓速器3D静态磁通密度分布如图5-14所示。分析磁通密度的目的是分析铁磁性材料中是否存在磁饱和现象。最可能存在磁饱和的地方是定子周期边界条件处。图5-15给出了图5-14中从A到B的磁通密度曲线。

图5-16所示为永磁缓速器3D模型在不同转速时的涡流密度分布。定子中涡流从永磁体输出边对应处流向相邻永磁体输入边对应处，或反之。从图中可以看出，涡流总是集中在永磁体输出边对应的定子部分，这部分磁饱和较严重。随着转速从600r/min增加到1800r/min，涡流密度变得越来越大。永磁体输出边对应的定子截面处的涡流密度等势线如图5-17所示。

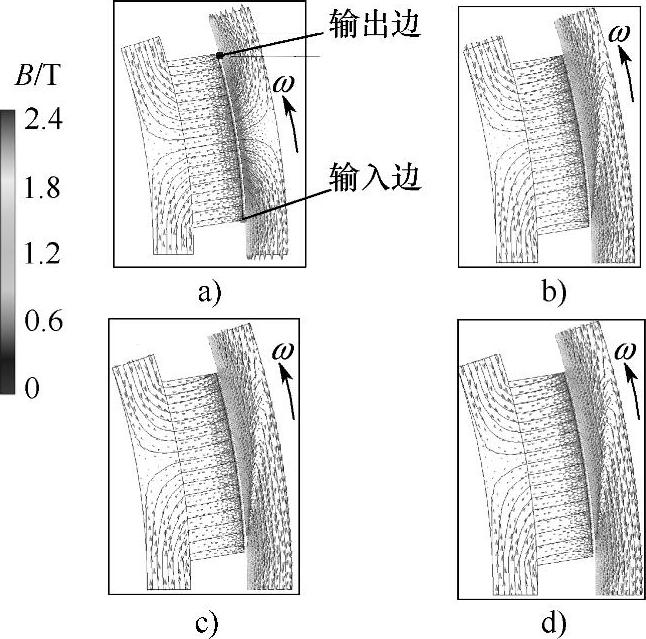
图5-12 缓速器在1000r/min时不同计算时间下的2D磁通分布

a）t=0.1s b）t=0.0006s c）t=0.0012s d）t=0.0024s

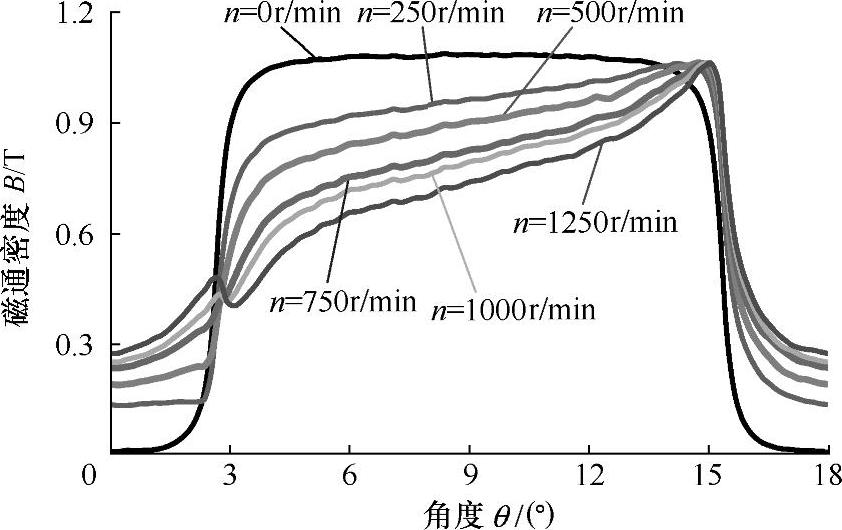
图5-13 不同转速时永磁缓速器3D模型的气隙磁通密度分布

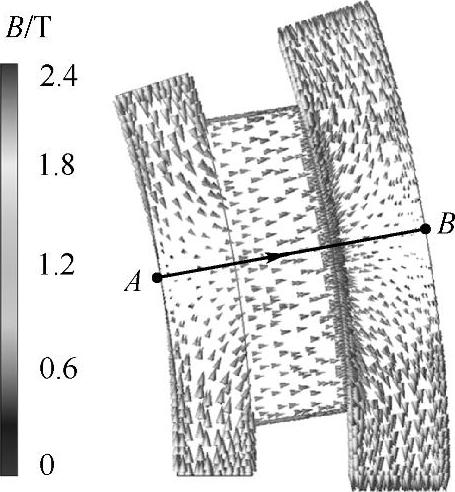
图5-14 永磁缓速器3D静态磁通密度分布

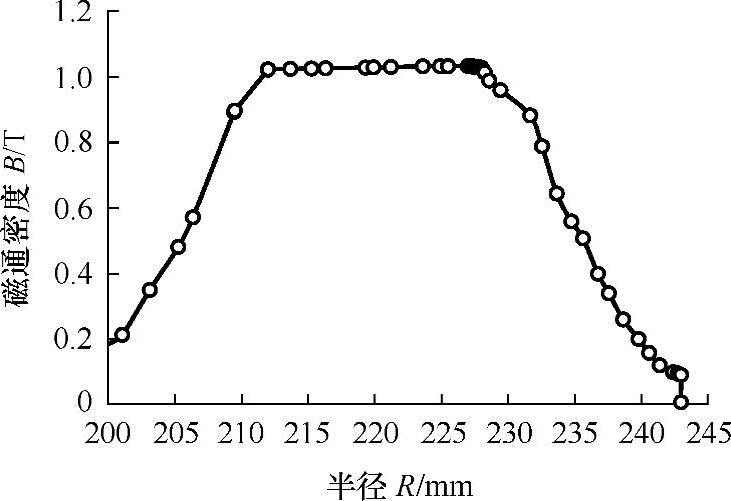
图5-15 A至B的磁通密度曲线(www.xing528.com)

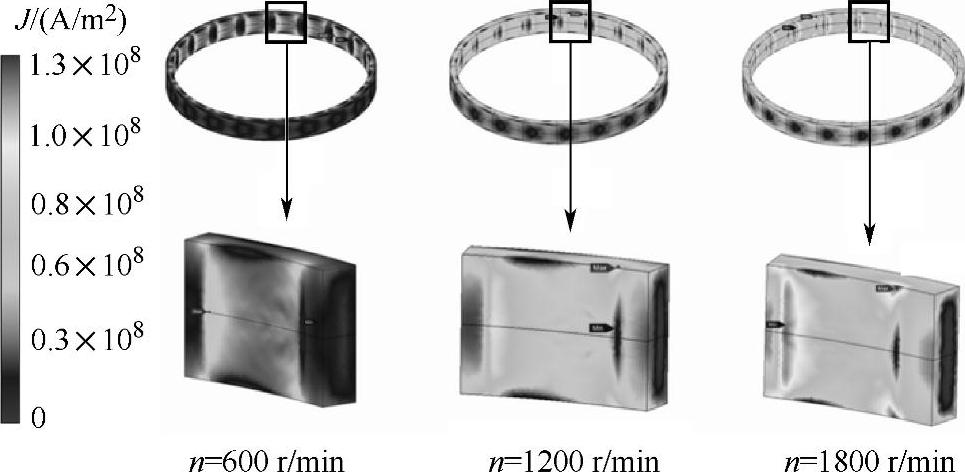
图5-16 永磁缓速器3D模型在不同转速时的定子涡流密度分布

转速为1000r/min时，定子上沿周向由A到B的涡流密度曲线如图5-18所示。涡流密度分布趋势与磁通密度是一致的。图5-19为定子上沿径向由A到B的涡流密度曲线所示，径向涡流密度分布趋势是符合趋肤效应公式的。

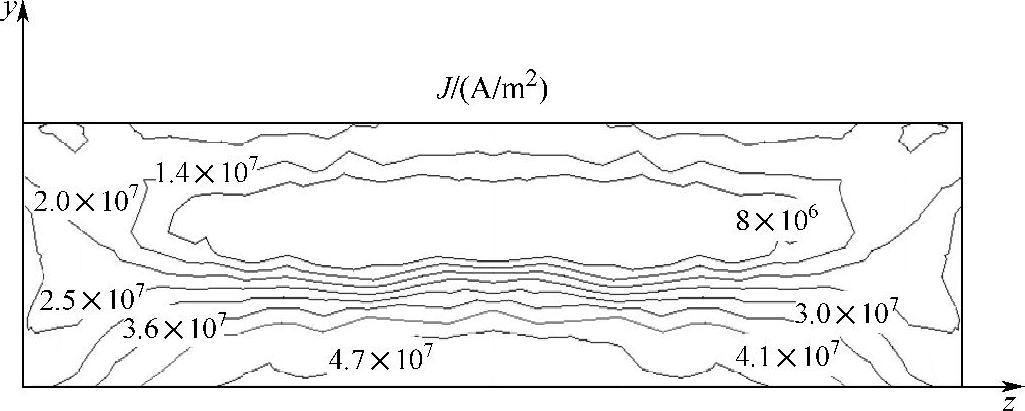
图5-17 永磁体输出边对应的定子截面处的涡流密度等势线

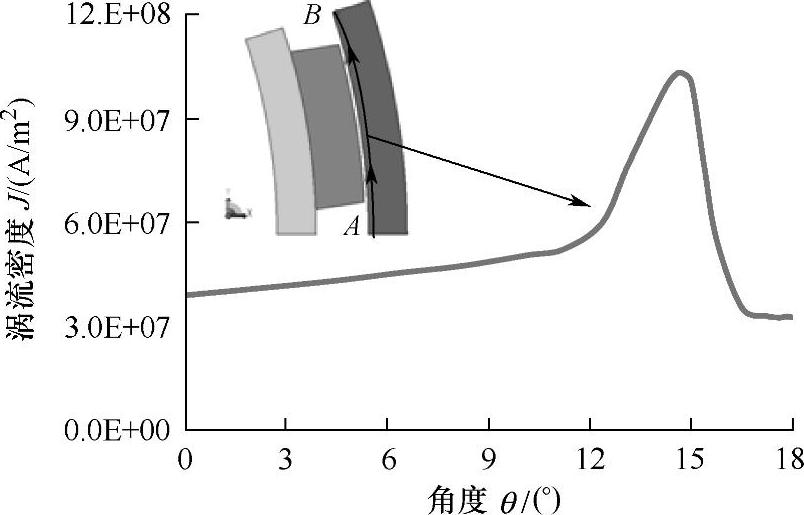
图5-18 定子上沿周向由A到B的涡流密度曲线

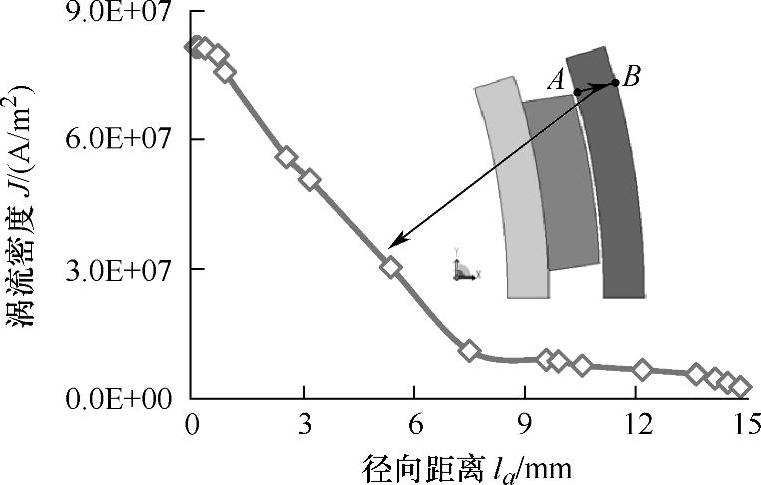
图5-19 定子上沿径向由A到B的涡流密度曲线

利用有限元法，计算了四种不同维数和步长组合的瞬态缓速器的制动力矩，如图5-20所示。经过若干次迭代后，在约0.01s时制动力矩计算达到稳定值。2D模型计算时未考虑定子端部的涡流效应，而3D模型揭示了定子端部涡流效应的重要性。根据表5-3，3D模型计算结果与试验吻合较好，计算误差很小。计算数据还表明，旋转角Δθ越小，CPU计算时间会越长，但是计算精度会越高。

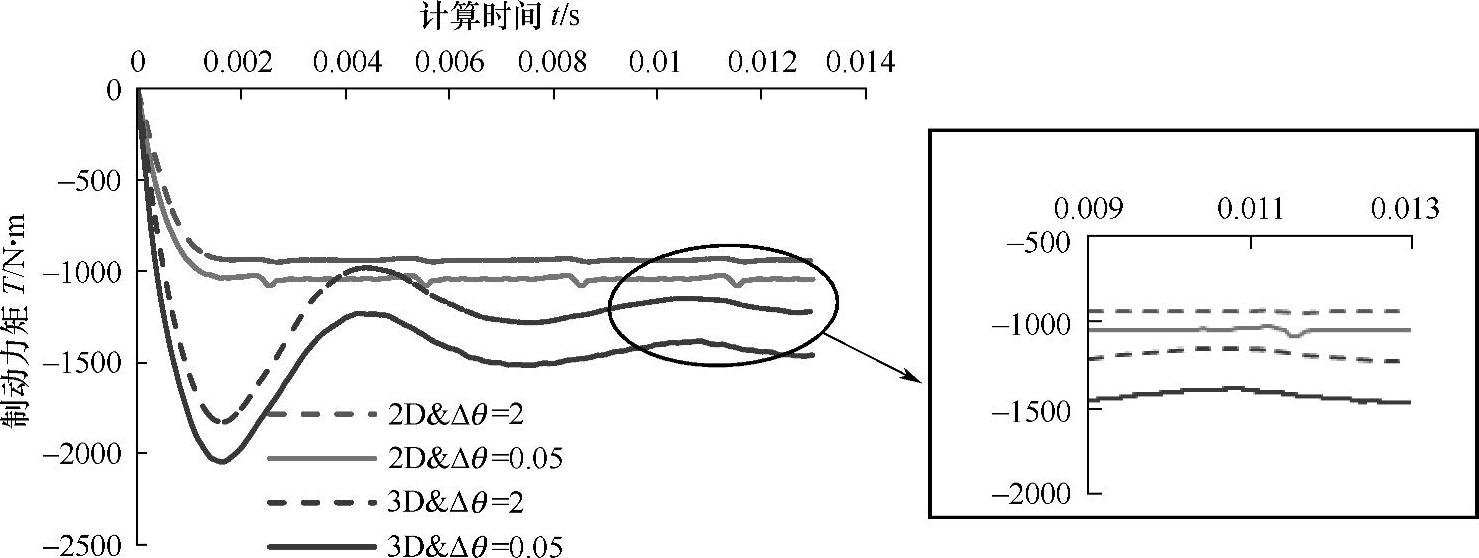
图5-20 瞬态缓速器有限元法制动力矩计算