合成气隙磁场的计算-先进汽车缓速器理论与试验

在沿x轴方向，距离中性面为X处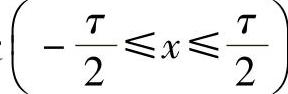，分析微分元dx内的电磁场。永久磁铁磁场B_y为平行于y轴、均匀分布的正弦磁场，故B_y可表达为

B_y=jB_y （4-40）围绕x=0的中性面，B_y可将在定子内感生电场强度E_z和涡流。根据法拉第电磁感应定律微分形式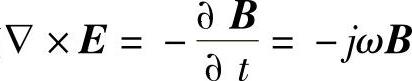可知

因此定子内涡流的电流密度J_z为

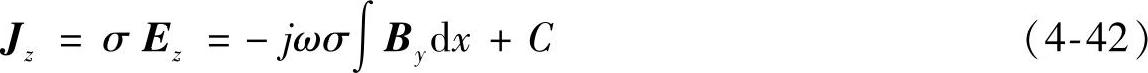
式中，常数C可根据涡流电流密度J_z的面积分等于0来确定，即

随着转子角速度的升高，由于趋肤效应，定子内表面感应的涡流密度在y轴上并不是一致的。此时磁场强度H_y将满足复涡流方程，即

上式的解答为

式中，A₁和A₂为任意常数；p为

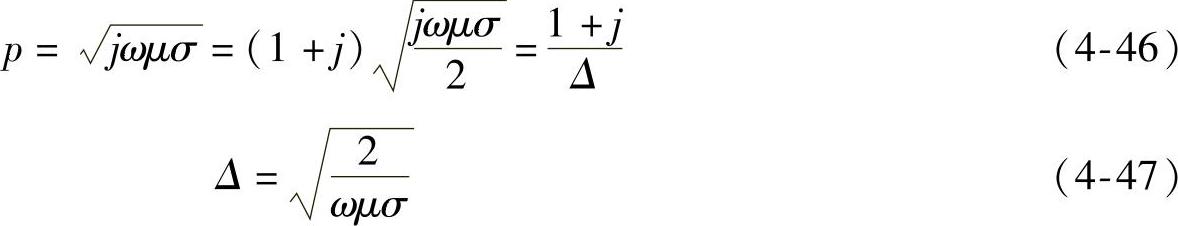
式中，Δ为趋肤深度。

当定子厚度h足够大时，H_y为有限，故A₂=0。在导体表面y=0处，H_y=H₀，故A₂=H₀。于是式（4-44）可改写为

(https://www.xing528.com)

而

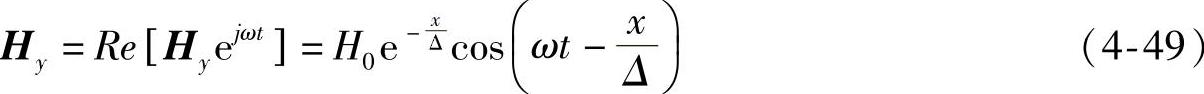
根据∇×H=J可知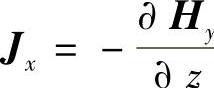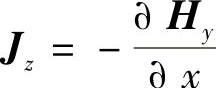，，；由于磁场强度H_y不随z变化而变化，故x方向的电流密度J_x=0，只有z方向的电流密度J（x，y）为

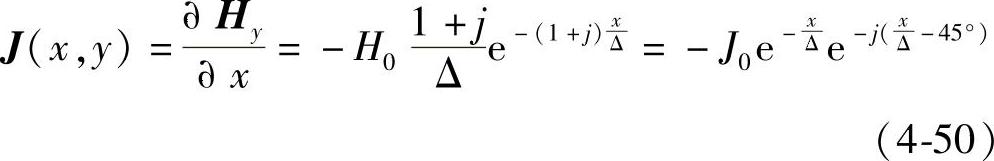
式中，J₀是定子内表面处的电流密度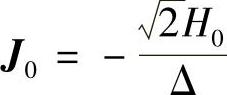，；则有

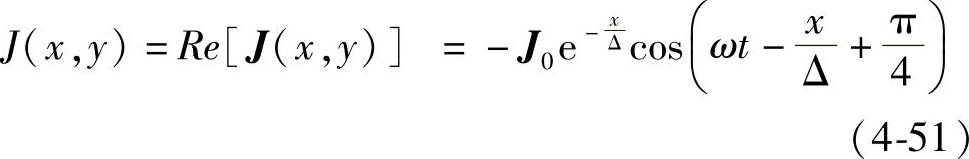
在转子刚开始运动的瞬间，设此时定子内感应涡流还未影响主磁场，即B_i=0。将式（4-35）代入式（4-39）并求解式（4-40）～式（4-50），可得到由磁场B₀感应的电流密度J₀。然后再将J₀带入式（4-36），利用迭代法计算式（4-30）～式（4-50），直至收敛，得到收敛后的B_i。图4-12给出了合成气隙磁通密度B_i的计算流程。

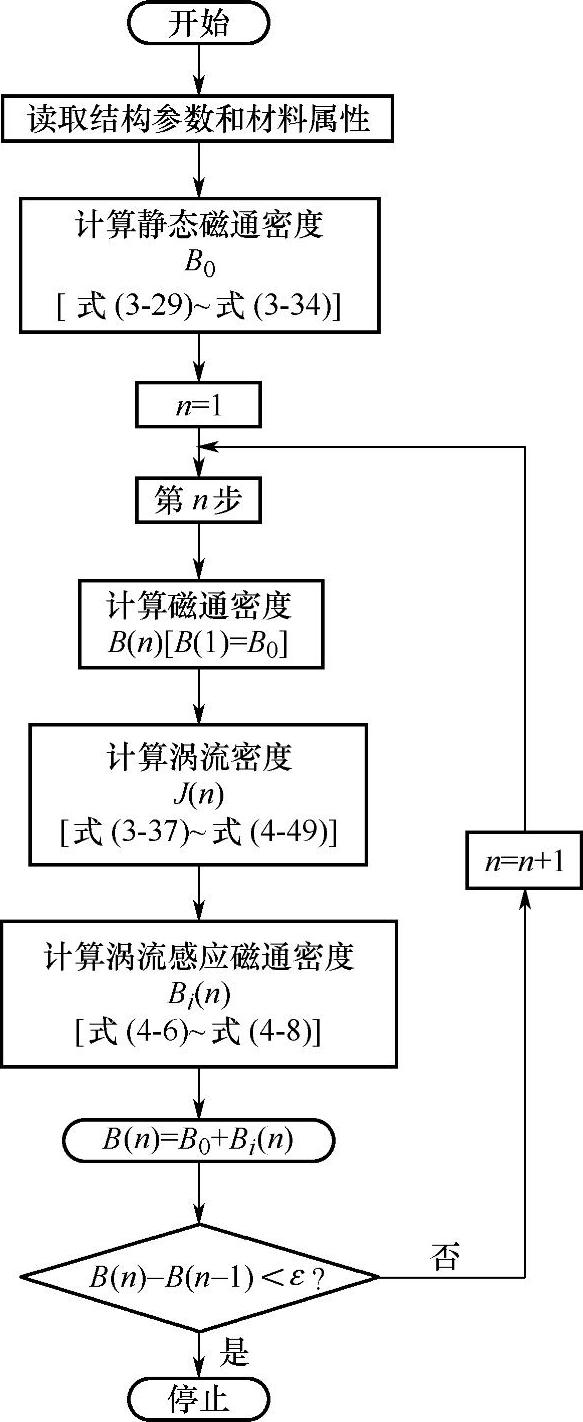
图4-12 合成气隙磁通密度B_i的计算流程

稳定工作时，永磁缓速器转子和永磁体内的磁场分布基本不变，定子内磁场以角速度ω随圆心旋转，形状不变。图4-13给出了瞬态时永磁缓速器内的磁场分布，从图中可以看出，在正对永磁体右侧（旋转方向的前方）的气隙磁场被涡流磁动势减弱，而左侧（旋转方向的后方）的气隙磁场被加强。图4-14给出了永磁缓速器瞬态时的合成气隙磁通密度分布曲线。

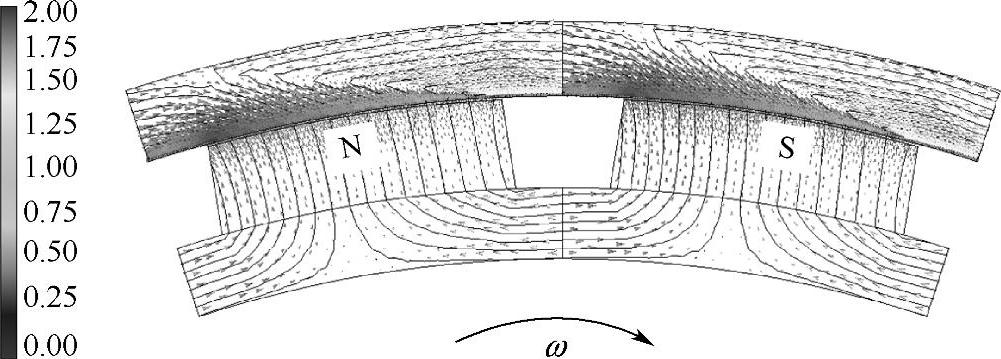
图4-13 瞬态时永磁缓速器内的磁场分布

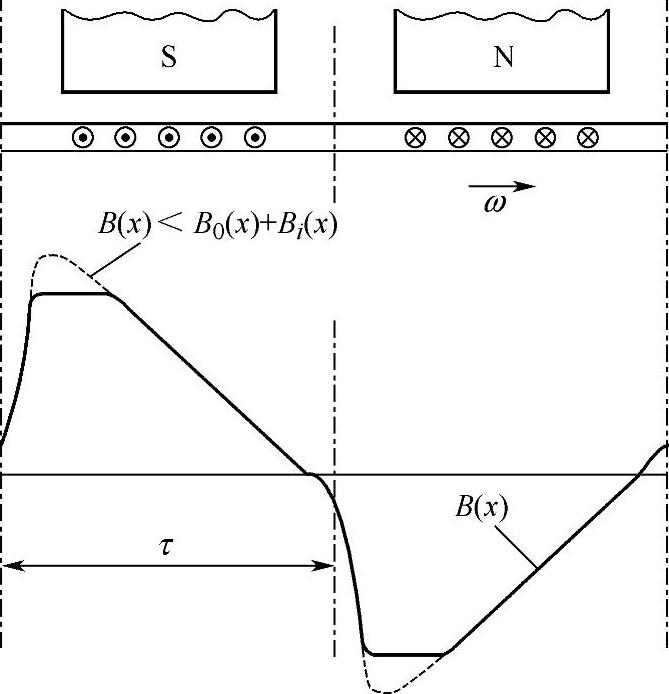
图4-14 永磁缓速器瞬态时的合成气隙磁通密度