磁场能量与电磁力实验成果

1.磁场能量

在n个线圈回路的磁场中，磁场能量表达为

式中 第k个回路的磁链为

所以n个线圈回路的磁场能量可表示为

当电流分布在媒质内，则由于JdV=IdI，上式可写为

根据Maxwell方程，上式可写为

根据前述矢量积的散度公式A·Δ×H=Δ·（H×A）+H·Δ×A，上式又可写为

应用高斯定理及B=Δ×A，上式成为

当积分扩展到无穷远处时，上式第一积分项为零，这样

磁场能量的体密度为

而对各向同性的线性媒质，磁场能量的体密度为

以上是线圈电磁场磁场能量和磁场能量体密度计算公式的导出过程。

2.电磁力

磁场能量以力和力矩形式应用于涡流制动装置中。磁场无论是由永磁体产生的还是由载流线圈产生的，由于运动电荷磁效应的作用，都将在磁场中产生两类磁场力或力矩作用，即载流导体在磁场中所受的磁场力和磁介质在磁场中所受的磁场力，有些文献分别称之为洛伦兹力和磁阻力。前者主要应用于电机、电磁仪表等设备和仪器中，后者则主要应用于各类永磁或电磁型磁力机械中。机器中应用这两类力及产生的力矩可实现能量转换、动力执行、运动传递等功能。

（1）Lorentz力 磁场对运动电荷产生的作用力为df=q（V×B），载流导体在磁场中所受到的力是导体内自由电荷所受力的总和。导体电荷体密度为σ，则q=σdV，而J=σv，所以df=σdV（V×B）=dV（J×B）。这样，单位体积载流导体受力（力密度）为

f=J×B （2-53）

当载流导体为线状时，电磁力为(www.xing528.com)

f=∫_lIdI×B （2-54）

洛伦兹力公式表达了电动机和一些电磁仪表的基本工作原理。

（2）磁阻力 介质在磁场中所受的磁场力（磁阻力）实质是磁场对介质磁化电流（分子电流）的作用。磁性介质磁化电流的体密度为J_m=Δ×M，在介质表面存在表面磁化电流，其面密度为J_S=-n×M。式中，M为介质的磁化强度，n为表面法向矢量。按上述电磁力计算公式，可得磁场对介质的作用力为

对于各向同性介质，上式可简化为f=∫_VM ΔBdV，磁场力的体密度为f=M ΔB。由于B=μ₀（H+M）和B=μ₀μ_rH，可得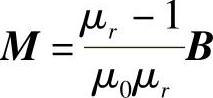，从而磁场对介质作用力的体密度为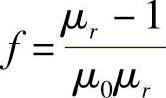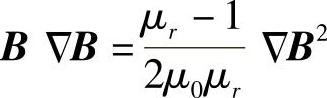。考虑介质中还有传导电流时，由于传导电流受力的密度f=J×B，因而总的力密度为

对于线性介质，设ρ为介质密度，则上式成为

上式物理意义如下：J×B为传导电流受力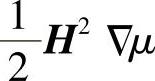；为磁介质内部和交界面处的μ的不均匀性引起的力，方向由μ值大处指向μ值小处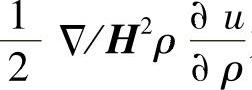；为磁介质内受力后发生变形使μ发生变化引起的力，通常称为磁致伸缩力。Faraday认为磁场中磁通管有沿纵向和横向的张力，两者大小相等，力密度为f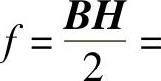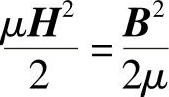。按此方法求解电磁力有时也称为Maxwell应力张量（MAXWELL STRESS TENSOR，以下简称MST）法。

另一种求解电磁力的方法是虚功（VIRTUAL WORK，以下简称VR）法。在n个线圈回路的磁场中，第k个回路的电流为I_k，磁链为ψ_k，当第i个回路在某一广义坐标上有虚位移dx、其他回路不动时，电源输入回路系统的净电能dW_e应等于磁场储能的变化dW_m与机械能的变化dWΩ之和，计算公式如下

dW_e=dW_m+dWΩ （2-58）

式中，。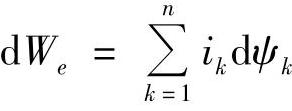

而机械能的变化为磁场力所做的功，设第i个回路的磁场力为f_i，则dWΩ=f_idx。代入上式中，得磁场储能的变化为

即磁场储能是独立变量ψ、x的函数，其表达式为

式中，ψ=（ψ₁，ψ₂，…，ψ_k，…ψ_n）。将W_m表达为全微分形式为

将其与磁场储能的变化式比较，可得

上式就是以ψ、x为独立变量表示磁场储能时磁场力的表达式。

当虚位移为角位移dθ时，磁场力变成磁场力矩