先进汽车缓速器物理场介绍

如果在全部空间或部分空间里的每一点，都对应着某个物理量的一个确定值，则称在这个空间里确定了该物理量的一个场。根据该物理量是数量或矢量，分别称该场为数量场或矢量场，根据该物理量在该场中各点处的对应值是否随时间变化而变化，将该场区分为稳定场和非稳场（时变场）。

数量场用数性函数来表示：u=u（x，y，z）。用等值面表示数量u在场中的分布状况。由场中使函数u取相同数值的点所组成的曲面称为等值面，如温度场中的等温面、电位场中的等位面等。

与数量场一样，矢量场中分布的矢量A是场中之点M的函数A=A（M）；在直角坐标系中，用其分量表示为A=A_x（x，y，z）i+A_y（x，y，z）j+A_z（x，y，z）k。每一点处，曲线都和对应于该点的矢量A相切的曲线称为矢量线，如静电场中的电力线、磁场中的磁力线、流场中的流线等，用矢量线可直观地表示矢量在场中的分布情况。

设有数性变量t和变矢A，如果对于t在某个范围G内的每一个数值，A都以一个确定的矢量与之对应，则称A为数性变量t的矢性函数，记为A=A（t），并称G为函数A的定义域。

在直角坐标系中，矢性函数A（t）的表达式为

A=A_x（t）i+A_y（t）j+A_z（t）k （2-1）

矢性函数有与数性函数类似的导数（导矢）、微分和积分，在直角坐标系中可通过其数性分量求取其微分与积分，计算公式如下

矢性函数广泛用于场的分析。

下面介绍数量场的方向导数和梯度。

1.方向导数

设M₀为数量场u=u（M）中的一点，从点M₀出发引一条射线l，在l上点M₀的邻近处取一动点M，记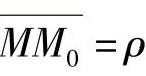。若当M→M₀时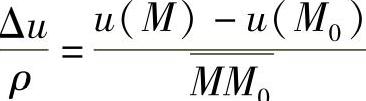的极限存在，则称它为函数u（M）在点M₀处沿l方向的方向导数，记为。

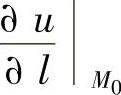在直角坐标系中，若函数u=u（x，y，z）在点M₀（x₀，y₀，z₀）处可微，cosα、cosβ、cosγ为l方向的方向余弦，则函数u在点M₀处沿l方向的方向导数必存在，如下

式中 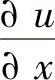、、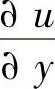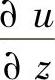——点M₀处的偏导数。

2.梯度

若在数量场u（M）中的一点M处，存在这样一个矢量G，其方向为函数u（M）在点M处变化率最大的方向，其模也正好是此最大变化率的数值，则称矢量G为函数u（M）在点M处的梯度，记为gradu，即gradu=G。

在直角坐标系中，梯度的表达式为

如把数量场中每一点的梯度与场中点一一对应，则得一矢量场，称为该数量场产生的梯度场。

下面介绍矢量场的通量、散度、环量和旋度。

1.通量

沿矢量场A（M）中的有向曲面S某一侧的曲面积分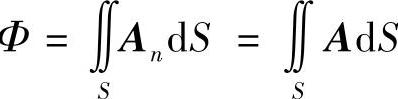称为矢量场A（M）向积分所沿一侧穿过曲面S的通量。

在直角坐标系中，设A=P（x，y，z）i+Q（x，y，z）j+R（x，y，z）k，则通量可写为(www.xing528.com)

2.散度

设有矢量场A（M），于场中一点M的某个邻域内作一包含M在内的任一闭曲面ΔS，设其所包围的空间区域为ΔΩ，以ΔV表示其体积，以ΔΦ表示从其内穿出S的通量。若当ΔΩ沿任意方式缩向M点时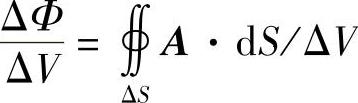，的极限存在，则称此极限为矢量场A（M）在点M处的散度，记为divA，是一数量。

散度由于是场中一点处通量对体积的变化率，所以又是该点处源的强度，其值为正、负或零时分别表示该点有正源（散发通量）、负源（吸收通量）或无源。

如把矢量场中每一点的散度与场中之点一一对应，则得一数量场，称为该矢量场产生的散度场。

在直角坐标系中，矢量场A=P（x，y，z）i+Q（x，y，z）j+R（x，y，z）k在任一点M（x，y，z）处的散度为

3.环量与环量面密度

设有矢量场A（M），则沿场中某一封闭的有向曲线l的曲线积分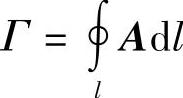称为此矢量场按积分所取方向沿曲线l的环量。

在直角坐标系中，矢量场A=P（x，y，z）i+Q（x，y，z）j+R（x，y，z）k的环量为

设M为矢量场A中的一点，在M点处取定一个方向n，再过M点任作一微小曲面ΔS，以n为其在M点处的法矢，对此曲面，又以ΔS表其面积，其周界Δl的正向取作与n构成右手螺旋关系，则矢量场沿Δl的正向的环量ΔΓ与面积ΔS之比，当曲面ΔS在保持M点与其上的条件下，沿着自身缩向M点时，若ΔΓ/ΔS的极限存在，则称其为矢量场A在点M处沿方向n的环量面密度，记为μ_n。

在直角坐标系中，环量面密度的计算公式为

式中，cosα、cosβ、cosγ为ΔS在点M处的法矢n的方向余弦。

4.旋度

若在矢量场A中的一点M处存在这样的一个矢量R，矢量场A在点M处沿其方向的环量面密度为最大，该最大的数值正好就是R，则称矢量R为矢量场A在点M处的旋度，记为rotA，即rotA=R。显然，旋度在数值和方向上表示出了最大的环量面密度。

在直角坐标系中，旋度的计算公式为

rotA=（R_y-Q_z）i+（P_z-R_x）j+（Q_x-P_y）k （2-10）

或

根据矢量场的Jacobi矩阵DA，可方便地求解矢量场的散度和旋度。

其对角线之和为散度，其余六个用于旋度公式中。

用矢量微分运算符Hamilton算子∇表达的梯度、散度和旋度，如gradu=∇u，divA=∇·A，rotA=∇×A。在以下的场量运算中将广泛地使用这些符号。

用Hamilton算子表达上述场量的一些重要性质，如∇·（∇×A）=0，∇×（∇×A）=∇（∇·A）-∇A，∇×（∇u）=0，∇·（A×B）=B·∇×A-A·∇×B等。