压弯构件板件的局部稳定设计准则-钢结构设计原理

1．不允许板件发生局部失稳的准则

不允许板件发生局部失稳的准则是令局部屈曲临界应力大于钢材屈服强度或大于构件的整体稳定临界应力。在实用上则将保证局部稳定的要求转化为对板件宽厚比的限制。

工字形截面（含H形）和箱形截面压弯构件的受压翼缘板，受力情况与相应梁的受压翼缘板相同，因此为保证其局部稳定性，所需的宽厚比限值可直接采用有关梁中的规定，但考虑对梁的塑性变形要求高、其受压翼缘板的宽厚比要求严，对压弯构件的受压翼缘板宽厚比要求可略放宽。

我国《钢结构设计标准》（GB 50017—2017）按此准则，限定翼缘和腹板的宽厚比应符合到压弯构件S4级截面要求，其具体如下。

工字形截面翼缘板自由外伸宽度b与其厚度ft之比应符合：

当截面设计时考虑有限塑性发展，则上式右端的15改成13。

箱形截面受压翼缘板在两腹板（壁板）间的无支承宽度0b与其厚度ft之比应符合：

当截面设计时考虑有限塑性发展，则上式右端的45改成40。

式（6.46）、式（6.47）中的 b、b0、ft等的含义见图 6.24 所示。图中也给出了腹板高度hw和厚度 tw的示意。

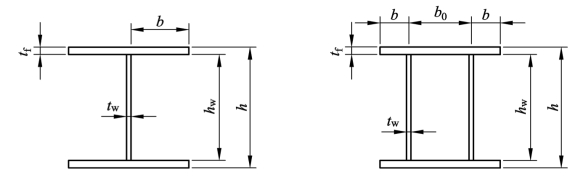
图6.24　宽厚比限值中的截面尺寸示意

腹板的宽厚比限值，按不同的截面形式分别予以规定。

1）工字形截面

我国设计标准中对工字形（含 H 形）截面压弯构件腹板的高厚比限值ww/h t是根据四边简支矩形板的稳定临界条件导出的。腹板在纵向承受不均匀压应力σ，在四周承受均布剪应力τ，如图 6.25 所示。在σ和τ的联合作用下腹板弹性屈曲临界状态的相关公式为：

式中：σ和τ分别为腹板边缘所受的最大压应力和均匀剪应力；α0为腹板所受压应力的应力梯度：

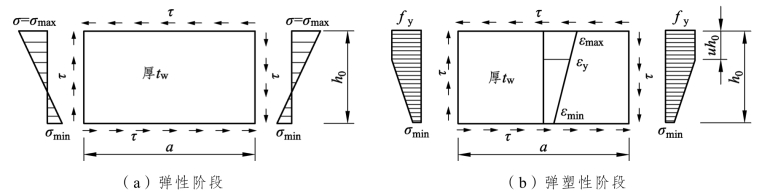
图6.25　四边简支矩形腹板边缘的应力分布

σmax和σmin均以压应力为正；α0=0时表示承受均布压应力，α0=2时表示为纯弯曲正应力；σ0、τ0为正应力或剪应力单独作用时的临界应力。从式（6.48）可见剪应力的存在，将降低压弯构件腹板在σ和τ联合作用下的临界压应力。在σ和τ联合作用下的弹性阶段临界压应力可表达为：

式中，ek为正应力与剪应力联合作用的弹性屈曲系数。它受腹的压应力梯度0α和与剪应力有关的系数影响。设定剪应力τ后，由相关公式（6.49）可求得不同应力梯度时的临界应力，亦即求得ke，从而根据式（6.50）得出不同梯度下的临界应力与hw/tw的关系。

此外还需考虑腹板在弹塑性状态下局部失稳的影响，此时截面的塑化常常扩展至腹板， 如图6.25（b）所示，此时的临界应力可写作：

式中，pk为正应力与剪应力联合作用下的弹塑屈曲系数，pk取值较为复杂，其影响因素有：应力比和板边缘的最大割线模量Es。割线模量Es又受腹板的塑性发展深度μh0影响，而腹板的弹塑性发展深度与构件的长细比是有关的。这里不对kp取值做深入讨论。根据这些因素，得到的腹板宽厚比限值将是参数α0,λ的复杂函数。 在制定设计标准时，对压弯构件的腹板，取τ为弯矩产生的正应力的 0.3 倍，即又取塑性发展深度为0.25h0。令式（6.51）中的σcr=fy，可求得并绘出随应力梯度0.15α0而变化的曲线。为了便于应用，设计标准GB 50017—2017 给出了简化计算公式，采用边缘纤维屈服准则时腹板的高厚比不应大于 S4级要求：

如考虑截面塑性发展，则腹板的高厚比不应大于S3级要求：

2）箱形截面

压弯构件腹板高厚比限值的规定与工字形截面相同，即式（6.52）为箱形截面单向压弯构件腹板为S4级截面的高厚比限值要求，式（6.53）为箱形截面单向压弯构件腹板为S3级截面的高厚比限值要求。

2．考虑利用屈曲后强度的准则

H形、工字形和箱形截面压弯构件的腹板，当其高厚比不能满足上述S4级截面要求时，可利用腹板屈曲后强度的准则进行设计，此时采用有效截面的概念，考虑局部失稳后的截面承载力和构件承载力。由于三边支承一边自由板屈曲后强度不高，工程上主要考虑四边支承板屈曲后强度的利用。有效截面面积的一种算法是：只考虑支承边附近各宽幅范围内的板有效，按此截面进行强度和构件整体稳定的计算，但计算构件长细比时截面回转半径仍可按毛截面取。有效截面面积的另一种算法与截面上的正应力分布有关，由于考虑屈曲后强度的复杂性，其采用准则尚未取得统一，因此不同的国家或同一国家的不同规范都会有不同的计算方法。下面介绍一种用于轻型钢结构的具体算法（图 6.26）。关于冷弯薄壁型钢结构中的计算方法可参阅有关规范。

图6.26　有效截面示意(www.xing528.com)

（1）计算腹板边缘的应力比ψ。

式中腹板边缘应力的符号规定同式（6.49）。

（2）计算受压高度系数ξ。

当ψ≥0时

当0ψ＜时

（3）计算受压腹板屈曲系数kσ。

当-1＜ψ≤-1 3时

当-1/3＜ψ≤1时

（4）确定受压范围的有效高度he。

当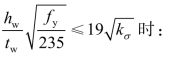

当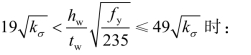

当

（5）确定有效高度he在受压范围两端的分布。

当ψ≥0时，即全腹板受压时：

根据所确定的有效宽度及其分布，重新计算截面的有效面积和有效截面模量，再进行各种计算。

式（6.54）～式（6.58）仅考虑了正应力引起的局部失稳后有效截面的计算。对工字形截面绕强轴单向压弯的构件，当截面上有剪力作用时，按边缘屈服准则，可以采用下列公式计算。

当V≤0.5Vd时：

当V＞0.5Vd时：

式中　Vd——考虑剪切作用下屈曲后强度的抗剪承载力。

式中　Weff,x,Aeff,x——按式（6.57）确定的有效截面模量和有效截面面积。

【例6.3】 验算例6.1中压弯构件的局部稳定性。

【解】 受压翼缘宽厚比限值：

腹板边缘最大压拉应力：

腹板宽厚比满足要求。