1.弯矩绕截面虚轴(记作x轴)作用的格构式压弯构件
双肢压弯格构式构件的截面一般是绕虚轴(通常记为x轴)的惯性矩和截面模量较大,该轴是弯曲轴。如图 6.19 所示。
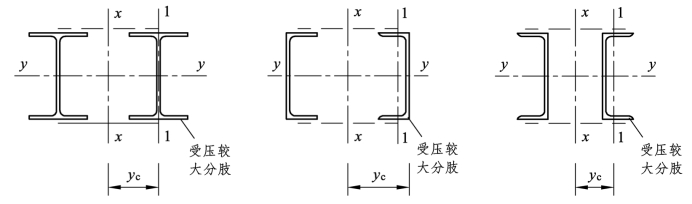
图6.19 格构式截面yc取值
(1)对弯矩作用平面内的稳定,采用考虑初始缺陷的边缘纤维屈服准则作为计算依据。验算条件为式(6.38b),即:

式中: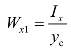 ,xI为截面对x轴的毛截面抵抗矩;cy为由x轴到压力较大分肢的轴线距离或到压力较大分肢腹板边缘的距离,两者中取其较大者,参阅图 6.19;轴心受压构件的整体稳定系数φx和
,xI为截面对x轴的毛截面抵抗矩;cy为由x轴到压力较大分肢的轴线距离或到压力较大分肢腹板边缘的距离,两者中取其较大者,参阅图 6.19;轴心受压构件的整体稳定系数φx和![]() 应由换算长细比λ0x确定,换算长细比的概念和计算方法详见轴压构件一章。
应由换算长细比λ0x确定,换算长细比的概念和计算方法详见轴压构件一章。
(2)弯矩作用平面外的稳定性,将转变为单肢在弯矩作用平面外的稳定计算。
格构式压弯构件两分肢受力不等,受压较大分肢上的平均应力大于整个截面的平均应力,因而还需对分肢进行稳定性验算。只要受压较大分肢在其两个主轴方向的稳定性得到满足,则整个构件在平面外的稳定性即可得到保证。
① 单肢稳定计算
当弯矩绕虚轴作用验算分肢稳定性时,缀条式格构式压弯构件分肢的轴心压力应按桁架中的弦杆计算,见式(6.39a),(6.39b)。对缀板式构件的单肢,除轴心压力外尚要考虑剪力引起的局部弯矩,如图 6.20 所示。
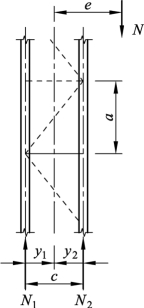
图6.20 格构式 构件单肢轴力计算

![]()
式中 e ——偏心距,可根据计算构件段的最大弯矩与轴力计算。
对缀条式构件的肢件,按轴心受力构件计算单肢在上述轴力作用下的稳定性。单肢在弯矩作用平面内的计算长度,取缀条体系节间的轴线距离;在弯矩作用平面外的计算长度,取两相邻侧向支承点之间的距离。
对缀板式构件的单肢,计算平面内稳定性时,尚要考虑剪力引起的局部弯矩。缀板式构件的剪力可取以下两式中的较大者:

式中 MΔ——缀板节间的弯矩增量;
a——缀板节间的轴线高度;
A——缀板式构件两肢件的毛截面面积之和;
fd——钢材强度的设计值。
确定剪力后,可根据图 6.21(c)的示意确定单肢上的弯矩,然后将一个节间的单肢视作压弯构件,计算其平面内稳定性。若缀板是焊接的,肢杆计算长度取两相邻缀板间净距;若缀板用螺栓连接,则取相邻两缀板最边缘螺栓间距离[图 6.21(a),(b)]。计算缀板式构件肢件在弯矩作用平面外稳定时,仍视为轴心压杆,计算长度取两相邻侧向支撑点间的轴线距离。
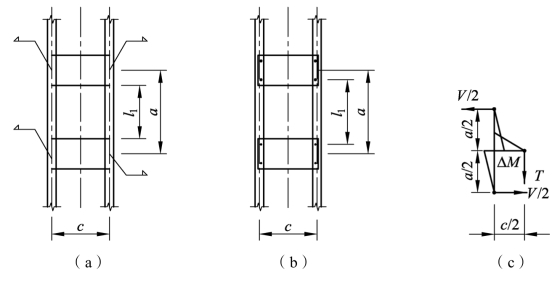
图6.21 缀板式构件单肢平面内计算长度及弯矩计算
② 缀条稳定计算
在缀条式格构构件中,缀条承受构件剪力引起的拉力或压力。对缀条受压,应按轴心压杆计算其稳定性。具体可参见轴压构件一章有关内容。
2.弯矩绕截面实轴(记作y轴)作用的格构式压弯构件
此时弯矩作用平面内外的稳定计算均与实腹式构件相同,按下式计算:

平面外稳定性计算按下式计算:

计算φx时长细比取绕虚轴x轴方向的换算长细比λ0x。φb取1.0。
3.弯矩作用在两个主平面内的双肢格构式压弯构件
这种构件的稳定性应按下列规定分两次计算。
1)按整体计算
计算公式为:

此式为公式(6.22b)等的推广,由于构件截面类似箱形,已取整体稳定系数φb=1.0。φx和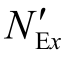 应按换算长细比确定。
应按换算长细比确定。
2)按分肢计算
首先,将构件所受轴心压力N和绕虚轴作用的弯矩Mx按桁架弦杆那样计算成分肢所受轴心压力N1和N2,即:

式中,h为两分肢轴线间的距离,h =y1+y2。
其次,将绕实轴y作用的弯矩My按照与分肢对y轴的惯性矩I1和I2成正比、与分肢至x轴的距离y1和y2成反比的原则进行分配。这样分配既可以保持平衡,又可保持变形协调。分肢1和分肢2所承受的弯矩为:
 (https://www.xing528.com)
(https://www.xing528.com)
最后,根据N1和My1、N2和My2分别对两个分肢按实腹式单向压弯构件计算其稳定性。
要指出的是:在实际工程中My如果是只作用在一个分肢的轴线平面内,则该My应全部由该分肢承受。例如图 6.22(a)所示柱截面若为单层厂房阶形柱的下部柱[见图 6.22(b)]的截面,因沿分肢轴线2-2设置吊车梁,前后两吊车梁上因荷载不等,对分肢2沿其轴线方向将产生My,此My即应由该分肢单独承受。
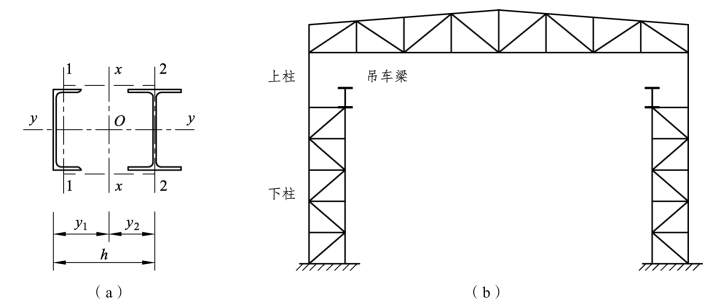
图6.22 双向弯曲的格构式压弯构件及单层厂房阶形柱下段柱
【例 6.2】 图 6.23 所示为一工业厂房柱,柱高 10 m,柱段的轴压力 N=2 000 kN,柱底弯矩Mx=800 kN ·m ,柱顶弯矩为0,弯矩作用平面内该柱为悬臂柱,弯矩作用平面外为两端铰接柱并在柱中部有侧向支承,钢材为 Q235。柱截面信息如下:柱肢为I45c,柱肢面积A1=120.446 cm2,Ix1=35 300 cm4,Iy1=938 cm4,ix1=17.1 cm ,iy1=2.79 cm ,Wx1=1 570 cm3,Wy1=122 cm3;缀条截面为└63×10,截面面积11.657 cm2,最小回转半径imin=1.22 cm。计算该构件的稳定性。
【解】 (1)截面几何性质计算。
截面面积:A=120.446 ×2 =240.892 (cm2)
截面形心:y0=50 cm
截面对虚轴的惯性矩及截面模量:
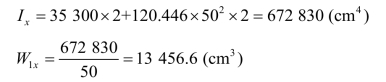

图6.23 例6.2图
回转半径:

虚轴方向长细比![]()
换算长细比: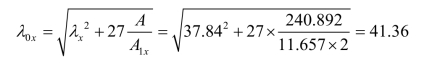
因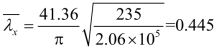 ,按轴心受压构件稳定系数计算公式得:
,按轴心受压构件稳定系数计算公式得:
![]()
(2)稳定性计算。
① 平面内整体稳定
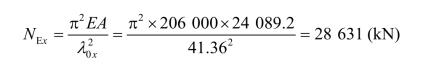
自由端与固定端的弯矩比m=0,则:

② 分肢稳定
柱子偏心距:
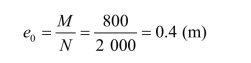
两分肢所受的轴力:
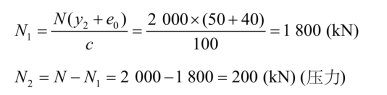
受压分肢在弯矩平面内的长细比:
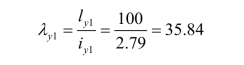
受压分肢在弯矩作用平面外的长细比:
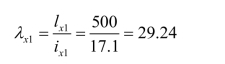
因轧制钢I45c翼缘宽与截面高度之比小于 0.8,其绕x1、y1轴的轴心压杆分类分别属于a、b 类,显然φy1有较小值。按轴心受压构件稳定系数计算公式得:
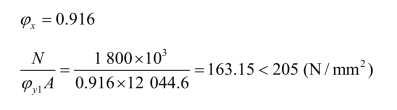
③ 缀条稳定
因斜缀条长于横缀条,且前者的计算内力大于后者,故只需演算斜缀条。
柱段计算剪力:
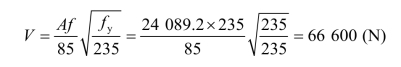
一个斜缀条受力:
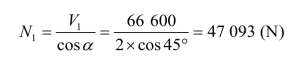
斜缀条长细比:
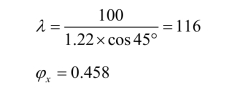
折减系数: γ0=0.6+0.001 5 ×116 =0.774
则
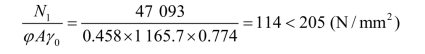
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




