钢结构设计原理：单向压弯构件的平面外整体稳定

当实腹式单向压弯构件在侧向没有足够的支承时，构件可能发生侧扭屈曲而破坏，其荷载-位移曲线如图 6.5（c）所示。由于考虑初始缺陷的侧扭屈曲弹塑性分析过于复杂，目前我国设计规范采用的计算公式的理论依据为理想的屈曲理论。

1．平面外弯扭屈曲的临界力

在弯矩作用平面外无初始几何缺陷（初挠度与初扭转）的双轴对称截面的压弯构件，其平面外失稳的平衡微分方程为：

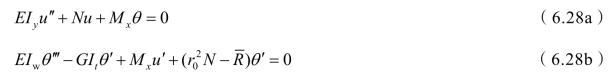
式中　Mx——端弯矩，Mx=Ney，ey为构件端部的偏心距。

平面外的侧移u和绕构件纵轴的扭转变形θ耦联出现，说明平面外整体失稳呈现弯扭状态，对于两端简支支承的构件，分别设解为，代入式（6.28）后得到：

式中　NEy——构件绕y轴弯曲屈曲的临界力

Nθ——构件绕z轴扭转屈曲的临界力

因构件失稳 c1和 c2不为零，故式（n）的系数行列式必须为零。由此看出，这一给定的问题具有屈曲问题的数学特征。令系数行列式为零得到：

或

由于

令Mx=Ney，则式（6.30）可以写为：

实际结构构件的情况远非如上各种规定那样简单理想，如果截面只有一个对称轴，扭转中心与截面形心不重合，平衡方程及其解的形式都会发生改变。此外构件比较粗短时，可能发生弹塑性失稳；构件有初始几何缺陷时，平面外稳定承载力也将成为极值型的问题；当构件截面单轴对称而弯曲平面不在对称轴平面内，或者截面无对称轴时，构件在截面两主轴方向的弯曲失稳和纵轴的扭转失稳将耦联在一起。在这些情况下，通常采用数值解法或试验方法来确定构件的失稳临界力。

2．平面外稳定承载力的实用计算公式

给定不同的Nθ/NEy值，式（6.31）可绘出N /NEy-Mx/Mcrx的相关曲线如图 6.17 所示，根据对常用截面形式的钢结构构件分析，一般情况下Nθ常大于N，因而该相关曲线均为向上凸。偏于安全近似采Ey的曲线形式依赖于系数用直线方程

图6.17　单向压弯构件平面外失稳的 相关曲线

作为构件平面外稳定与否的判别式。

以φy Afy和φbWxfy分别替换NEy和Mcrx，并考虑实际荷载情况不一定都是均匀弯曲引入侧扭屈曲时的等效弯矩系数βtx，代入式（6.32），得到：

在工程设计中，用强度设计值fd代替屈服点fy，并考虑到闭口截面的情况，引入截面影响系数 η，则上式即成为规范中关于弯矩作用平面外的稳定性计算公式：

式中　φy——弯矩作用平面外的轴心受压构件稳定系数，要注意当为单轴对称截面时，φy值应按计及扭转效应的换算长细比λyz查取；

φb——均匀弯曲时的受弯构件整体稳定系数，对工字形截面和 T 形截面，φb可采用如下近似公式：

（1）工字形截面

① 双轴对称时（含H型钢）

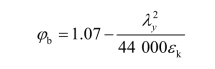
② 单轴对称时

（2）弯矩作用在对称轴平面，绕x轴的T形截面

① 弯矩使翼缘受压时

双角钢T形截面　φb=1 -0.001 7λy/εk

部分T形钢和两板组合T形截面φb=1 -0.002 2λy/εk

② 弯矩使翼缘受拉且腹板宽厚比不大于18εk时

上述公式计算的φb＞1时，取φb=1

对闭口截面，φb=1.0(www.xing528.com)

η——截面影响系数，闭口截面时取0.7，其他截面取1.0；因闭口截面的抗扭刚度特别大，取η=0.7，实际上这是一个经验修正系数，由对箱形截面侧扭屈曲的理论分析比较后得出；

Mx——所计算构件段范围内的最大弯矩设计值；

βtx——计算平面外稳定时的弯矩等效系数，分两类按4种情况取值：

（1）在弯矩作用平面外有侧向支承的构件，应根据两相邻支承点间构件段内的荷载和内力情况确定：

① 构件段无横向荷载作用时

M1和M2是构件段在弯矩作用平面内侧向支撑点处的端弯矩，使构件段产生同向曲率时取同号，反之取异号，且

② 构件段内有端弯矩和横向荷载作用时

使构件段产生同向曲率，βtx=1.0

使构件段产生反向曲率，

③ 构件段内无端弯矩但有横向荷载作用时

（2）弯矩作用平面外为悬臂构件：

【例6.1】 某H型等截面钢柱材料为 Q345，设计强度f=305 kN/mm2，柱高及截面尺寸如图 6.18 所示，轴心受压构件截面分类对x轴为b类，y轴为c类；截面塑性发展系数γx=1.05，γy=1.2；钢柱上的轴力和弯矩分布如图，构件上考虑作用有端弯矩，无横向荷载；在弯矩作用平面内，计算长度l0x=18 m ，为有侧移框架；在弯矩作用平面外，无侧移框架，柱顶柱底均为铰接，在距柱底6.5 m处有一平面外支撑，上柱和下柱的计算长度系数均为uy=1。上柱弯曲整体稳定系数φb=0.945 7，下柱弯曲整体稳定系数φb=0.799 9。假定构件的不发生板件局部失稳，验算压弯构件的承载力。

图6.18　例6.1图

【解】 （1）截面特性计算。

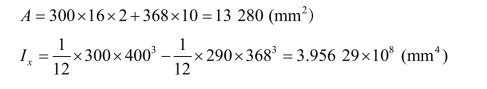
（2）内力计算。

（3）轴压构件稳定承载力计算。

x轴：

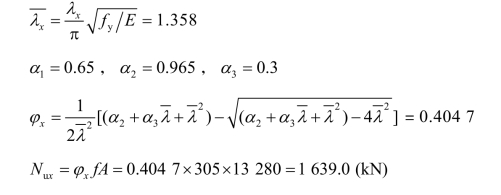
y轴：

上柱

下柱

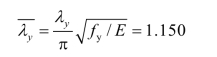
（4）受弯构件整体稳定承载力计算。

（5）压弯构件平面内整体计算。

平面内，为有侧移框架，βmx=1，则：

平面内稳定承载力满足要求。

（6）压弯构件平面外整体计算。

牛腿以上柱段：

上柱平面外稳定承载力满足要求。

牛腿以下柱段：

下柱平面外稳定承载力满足要求。