单向拉弯或压弯构件截面强度-《钢结构设计原理》

下面根据不同的计算准则，以单向拉弯构件为例说明单向拉弯或压弯构件的截面强度关于轴力N和弯矩M的相关关系。

1．按边缘纤维屈服准则计算时的强度

构件在轴心拉力N和绕一个主轴x轴的弯矩xM作用下，在最危险截面上，截面边缘处的最大应力达到屈服点时（图 6.6），拉弯构件的强度计算公式为：

或

式中　N，Mx——验算截面处的轴力和弯矩；

A——验算截面处的截面面积；

Wx——验算截面处的绕截面主轴x轴的截面模量；

Np——屈服轴力，NP=Afy；

Mex——屈服弯矩，Mex=Wxfy。

图6.6　单向拉弯构件应力分布

2．按全截面屈服准则计算时的强度

在轴力和弯矩共同作用下全截面进入塑性时，截面上应力分布不仅与轴力N、弯矩 M 的大小有关，也和构件截面形状有关。图 6.7 表示双轴对称工字形截面拉弯构件绕强轴x轴受弯时，中和轴在腹板内的全截面达到塑性时的压应力分布，腹板受压屈服区的高度为0ch，相应受拉区高度为(1-c )h0。

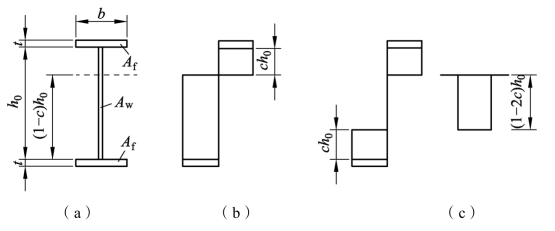
图6.7　单向拉弯构件全截面屈服时的应力分布

将应力图分解为与Mx［图 6.7（b）］和 N［图 6.7（c）］相平衡两部分，由平衡条件得：

式中　Aw——腹板面积，Aw=h0tw；

Af——翼缘板面积，Af=bt。

以上两式消去 c，得：

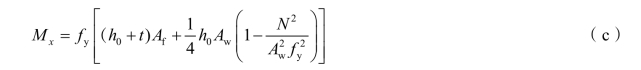
令

则

式中

截面完全受拉而屈服时：

截面完全受弯而屈服时：

(www.xing528.com)

将以上关系式代入式（c）得：

若设α=Aw/2Af,β=t /h0，则式（i）可写为：

若中和轴在翼缘内，依同样原理可得：

当绕弱轴弯曲时，中和轴在腹板内，其表达式为：

中和轴在翼缘内，其表达式为：

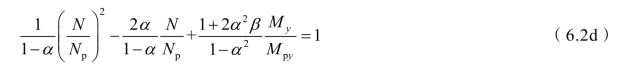
图 6.8 绘出工字形截面在通常比例尺寸情况下-N M相关曲线的范围，从图中可以看出，曲线均向外凸，对于其他形式截面也是一样。在设计中为了简化，可以偏安全地采用直线关系式（即图6.8中虚线），其表达式为：

式中　Wp——截面塑性模量。

以Np=Afy和Mp=ηWxfy，代入式（6.3），可得：

图6.8　拉弯或压弯构件截面极限 强度相关曲线

式中，η 是截面形状系数，对矩形截面为 1.5，对工字形截面为1.10～1.17。

对于工字形截面绕强轴弯曲的情况，若要求比式（6.3）更好的近似程度，可以采用两直线来代替，其表达式为：

当

当

3．按部分发展塑性准则计算时的强度

构件在轴力和弯矩作用下一部分截面进入塑性，另一部分截面还处于弹性阶段时（图6.9），其应力分布将介于弹性和全截面屈服之间。

从式（6.1）和式（6.3）可以看出，轴力N和弯矩M都是直线关系，两式差别在左端第二项，式（6.1）采用弹性截面模量W，应力处于弹性阶段，式（6.3）采用塑性截面模量pW，应力处于全截面塑性阶段。考虑到塑性变形在截面上的发展深度过大，将导致较大的变形，以及考虑截面上剪应力的不利影响，把式（6.4）中的η改为截面塑性发展系数xγ，因xγ η＜，应力处于弹塑性时，也可采用直线关系式，即：

图6.10表示式（6.1）、式（6.2）、式（6.3）、式（6.5）、式（6.6）的-N M曲线，从中可以看出拉弯或压弯构件不同计算公式之间的关系。

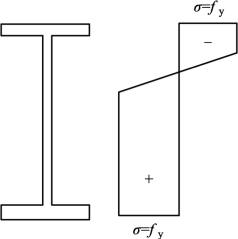
图6.9　单向拉弯构件截面弹塑性应力分布

图6.10　工字形截面N-M曲线