拉弯和压弯构件破坏形式分析

拉弯或压弯构件的破坏形式有强度破坏、整体失稳破坏、局部失稳破坏和刚度不足导致变形过大等。

强度破坏指截面的一部分或全部应力都达到甚至超过钢材屈服点。内力最大的截面、等截面构件中因孔洞等原因局部削弱较多的截面、变截面构件中内力相对大而截面相对小的截面可能首先到达这一状况。图6.4给出了单向压弯构件截面应力发展情况的一例。

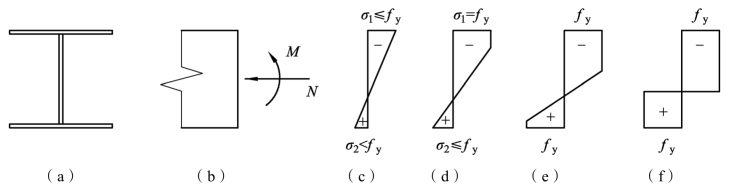
图6.4　单向压弯构件截面的应力发展

压弯构件的整体失稳破坏有多种形式。单向压弯构件的整体失稳分为弯矩作用平面内和弯矩作用平面外两种情况。

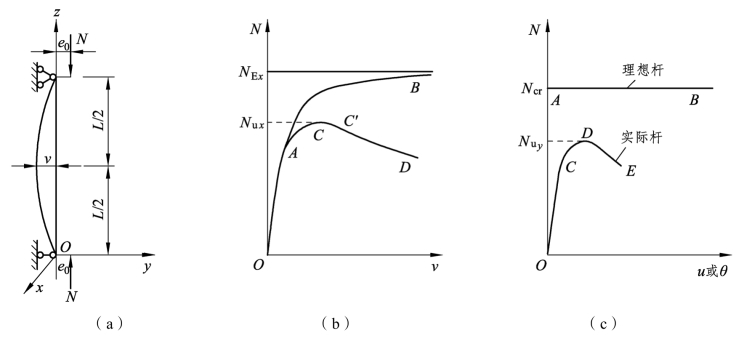
图6.5　单向压弯构件的轴力-位移曲线(www.xing528.com)

图 6.5（a）表示一单向偏压构件，两端铰支，偏心轴力 N 作用在构件截面的对称轴所在的平面yOz内。如足够的约束防止构件发生弯矩作用平面外的位移，则构件受力后只在弯矩作用平面内发生弯曲变形。图6.5（b）表示压弯构件平面内跨中最大横向位移 v 与构件压力 N 的关系曲线。从图中可以看出，压弯构件在弯矩作用平面内不存在分枝现象，这与理想轴心压杆不同。在进行结构分析时，多数情况下变形足够小，只考虑内外力在结构初始位置下的平衡，当然也不考虑初始几何缺陷等的影响，即采用一阶分析。压弯构件平面内失稳则与轴力引起的“二阶效应”有关，即需要考虑轴压力对杆轴水平变位δ所产生附加弯矩的影响，通常将其称为 P-δ 效应。压弯构件在轴力和弯矩作用下按一阶分析得到的横向变位为0δ，轴压力N在其上引起的弯矩Nδ0又造成横向变位增量1δ，从而导致轴压力N与变位v的关系呈现非线性。加载初期构件处于弹性工作阶段，N-v接近线性变化。当荷载逐渐加大，曲线在 A 点开始偏离直线。若材料为无限弹性，则此曲线为OAB，在N接近于欧拉荷载NEx时，v趋向无限大；事实上杆长为l，决定了构件的横向变形v不可能无限大，同时钢材为弹塑性材料，其N-v曲线不可能为OAB，而将沿OACD变化。曲线AC段时的构件截面虽已进入弹塑性阶段，但v仍随着N的加大而加大，此时构件内、外力矩的平衡是稳定的。曲线CD段时，构件截面塑性区不断扩展，截面内力矩已不能与外力矩保持稳定的平衡，因而这阶段是不稳定的，并在减小荷载情况下位移 v 不断增加。图中的 C点是由稳定平衡过渡到不稳定平衡的临界点，也是曲线 OACD 的极值点，相应于 C 点的轴力Nux称为极限荷载、破坏荷载或最大荷载。荷载达到Nux后，构件即失去弯矩作用平面内的稳定（称为平面内失稳），这类失稳被称为极值失稳。曲线在极值点之后的部分称为下降段或负刚度段。需要注意的是，在曲线的极值点，构件的最大内力截面不一定到达全塑性状态［如图 6.4（f）］，而这种全塑性状态可能发生在轴压承载力下降段的某点 C′ 处。

如果构件在平面外没有足够的侧向支承，对无初始缺陷的理想构件，当荷载较小时构件在 yOz 平面内弯曲，不产生沿x轴方向的出平面位移u和绕z轴的扭转变形θ；若构件的平面内稳定性较强，则轴力 N 加到Ncr后则突然产生平面外的侧扭屈曲而破坏，其平面外的变形关系如图 6.5（c）中的OAB线所示，这种失稳具有屈曲失稳的特点。若构件具有初始缺陷，则荷载一旦施加，构件即可产生较小的位移u和扭转变形θ，如图 6.5（c）中的OC 线所示。随着荷载的增大，变形 u 和θ逐渐加大，待到达某一荷载Nuy后，变形 u 和θ会突然增加很快，只有减小轴力 N 构件才能平衡，如图 6.5（c）中的 DE 线所示，构件发生侧扭屈曲而破坏（称为平面外失稳）。Nuy是发生侧扭屈曲时的极限荷载。

从上面分析可见，对单向压弯构件的平面内失稳为弯曲失稳，平面外的失稳为弯扭失稳。而双向压弯构件的整体失稳一定伴随着构件的扭转变形，这是与双向弯曲显著不同的变形特征。

局部失稳发生在压弯构件的受压翼缘和腹板，或有较大剪力作用的腹板。局部失稳对构件的影响，可以参考有关轴心受力构件和受弯构件的叙述。

压弯构件变形太大，会妨碍构件正常使用，导致依附于压弯构件的其他部件损坏，工程设计时通常限制构件的挠曲变形和构件的长细比来控制。

由上可见对单向压弯构件必须分别验算截面强度、平面内稳定和平面外稳定两种稳定性、局部失稳、构件刚度。双轴对称截面压弯构件平面内稳定为弯曲失稳，平面外稳定为弯扭失稳。双向压弯构件则只有弯扭失稳一种可能。