钢结构设计原理：组合梁设计

1．截面尺寸拟定

组合梁一般常用两块翼缘板和一块腹板焊接成双轴对称工字形截面，截面尺寸拟定就是要根据受载拟定出如图 5.34 所示的各截面尺寸。

1）截面高度

确定梁的截面高度应综合考虑建筑要求、刚度条件和经济性。

（1）建筑要求，即建筑允许的最大梁高，又称建筑高度，它是指梁的底面至铺板顶面之间的高度（对公路桥梁来讲指梁底至行车面之间的高度，对铁路桥来讲指梁底至轨顶之间的高度）。它限定了梁的最大高度hmax。

（2）刚度条件，是要求梁在全部荷载标准值作用下的挠度不大于容许挠度。对于给定跨度的梁来讲，荷载作用下的挠度与梁的高度密切相关，梁越高，荷载作用下的挠度也就越小；限定了最大挠度也就限定了最小梁高，因此刚度条件决定了梁的最小高度minh。

梁的刚度条件即应使梁在全部荷载标准值作用下的挠度v不大于容许挠度[v]。对于等截面简支梁：

图5.34　工字形组合截面

式中　σk——全部荷载标准值产生的最大弯曲正应力。

若梁的抗弯强度σ接近设计强度f，可令σk=f /1.3，这里1.3为近似的平均荷载分项系数。由此得梁的最小高跨比的计算式：

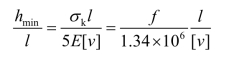
可见，梁的容许挠度越小，则梁所需截面高度越大；选择钢材的强度越高，要做到刚度满足的同时充分发挥钢材的强度，梁所需截面高度就越大。

（3）经济梁高eh。一般来说，腹板的用钢量会随梁的高度增加而增多，而翼缘板的用钢量则随梁的高度增加而相对减少，最经济的截面高度应使梁的总用钢量为最小。设计时可参照下列经济高度的经验公式初选截面高度：

式中　Wx——梁所需要的截面模量，

从经济条件出发，可以确定用钢量最少时对应的一个梁高，即经济梁高。

根据上述三个条件，实际所取用的梁高h一般应满足：

2）腹板高度wh

梁翼缘板的厚度t相对较小，腹板高度wh较梁高h小得不多。因此，当梁的截面高度h初步确定后，梁的腹板高度hw可取稍小于梁高h的数值，并尽可能考虑钢板的规格尺寸，将腹板高度hw取为 50 mm 的整数倍。

3）腹板厚度tw

梁的腹板主要承受剪力作用，可根据梁端最大剪力确定所需腹板厚度。在梁端翼缘有削弱的情况下，可取：

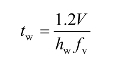
根据最大剪力所算得的tw一般较小。设计时，腹板厚度亦可用下列经验公式估算：

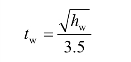
式中，tw和hw的单位均以 mm 计。

实际采用的腹板厚度应考虑钢板的规格，一般为 2 mm 的整数倍。对于承受静力荷载的板厚度取值宜比上两式的计算值略小；对考虑腹板屈曲后强度的梁，腹板厚度可更小，但腹板高厚比不宜超过k250ε。

4）翼缘板尺寸

翼缘板尺寸可以根据需要的截面模量和腹板截面尺寸计算。

梁的截面惯性矩

因此可得：

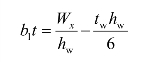
算出一个翼缘板需要的面积b1t后，再选定翼缘板宽度b1和厚度t中的任一数值，即可求得另一数值。一般翼缘宽度b1取值：

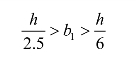
因此，可以根据使用要求初选宽度b1，再求出厚度t。

当宽度b1和厚度 t 初步选出后，首先应检查是否满足局部稳定要求，梁受压翼缘的外伸宽度 b 与厚度 t 的比值应满足：

若能把 b/t 限制在13εk以内，则可以使部分截面发展塑性（取γx=1.05），往往可取得较经济的效果。

2．截面验算

首先根据初选的截面尺寸进行实际截面的几何特性计算，如截面惯性矩、截面模量和截面面积矩等，然后按照与型钢梁截面验算基本相同的方法进行下列各项验算。验算中应注意，如初选截面时未包括自重作用，则此时应加入梁自重所产生的内力。

（1）抗弯强度验算。

（2）抗剪强度验算。

（3）局部承压强度验算。

（4）折算应力验算。

（5）整体稳定验算。

（6）局部稳定验算。

（7）刚度验算。

（8）对于承受动力荷载作用的梁，必要时应按《钢结构设计标准》规定进行疲劳验算。

3．组合梁变截面设计

梁的截面往往以抗弯强度控制设计，而梁的弯矩又沿梁跨变化，故梁的截面能随弯矩在梁跨方向的变化而变化则可节约钢材。对小跨度梁采用变截面时，加工量会增加，经济效果不明显，故仍采用等截面设计。对大中跨径梁改变一次截面一般可节约钢材 10%～15%，如再设置一次变截面，则节约钢材不多，所以通常只改变一次变截面。

梁截面变化的方式有两种，一是变翼缘尺寸（如图 5.35、图 5.36 所示），二是变梁高（如图 5.37 所示）。在建筑工程结构中，常采用的是第一种方式，它又可分为变翼缘宽度和变翼缘厚度两种方法。

对承受均布荷载的梁，截面改变位置在距支座1/6跨径处最有利，较窄翼缘板宽度tb′应由截面开始改变处的弯矩1M确定。为减小应力集中，宽板应从截面开始改变处向一侧以不大于1∶2.5（动力荷载时不大于1∶4）的斜度放坡，然后与窄板对接。

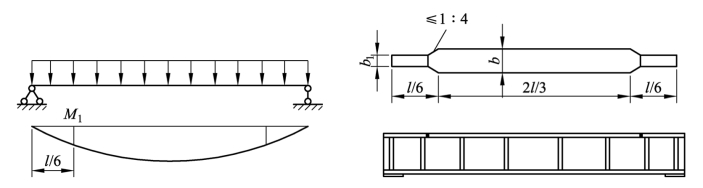
图5.35　梁翼缘宽度的改变

图5.36　多层翼缘板的截断

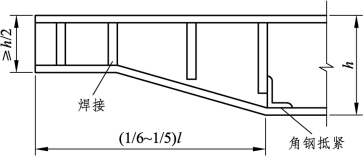
图5.37　变梁高

单层翼缘板的焊接梁改变截面时，宜改变翼缘板的宽度而不改变其厚度。

多层翼缘板的梁，可用切断外层板的办法来改变梁的截面。理论切断点的位置可由计算确定。为了保证被切断的翼缘板在理论切断处能正常参加工作，其外伸长度l1应满足下列要求：

端部有正面角焊缝

当

当

端部无正面角焊缝 l1≥2b1

式中：b1和t1分别为被切断翼缘板的宽度和厚度；hf为侧面角焊缝和正面角焊缝的焊脚尺寸。

为了降低梁的建筑高度，简支梁可以在靠近支座处减小其高度，而使翼缘截面保持不变（如图 5.37 所示），梁端部高度应根据抗剪强度需要确定，但不宜小于跨中高度的1/2。

4．焊接组合梁翼缘焊缝的计算

当梁弯曲时，由于相邻截面上作用在翼缘上的弯曲正应力有差值，翼缘与腹板间将产生水平剪力，该水平剪力即由翼缘与腹板间的焊缝承受，如图 5.38。

图5.38　翼缘与腹板间焊缝的水平剪力

沿梁单位长度的水平剪力：

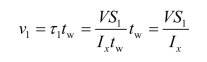
式中　τ1——腹板与翼缘交界处的水平剪应力；

S1——翼缘截面对梁中和轴的面积矩。

当腹板与翼缘板采用角焊缝连接时，角焊缝有效截面上承受的剪应力fτ，不应超过角焊缝强度设计值，即：

需要的焊脚尺寸：

当梁的翼缘上受有固定集中荷载而未设置支承加劲肋时，或受有移动集中荷载（如吊车轮压）时，上翼缘与腹板之间的连接焊缝，除承受沿焊缝长度方向的剪应力τf外，还承受垂直于焊缝长度方向的局部压应力：

因此，受有局部压应力的上翼缘与腹板之间的连接焊缝应按下式计算强度：

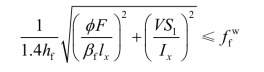
从而

对直接承受动力荷载的梁，βf=1.0；对其他梁，βf=1.22。

【例5.4】 某工作平台采用梁格布置，如图 5.39 所示，次梁间距 2 m，主梁间距 5 m。铺板为钢筋混凝土板，与次梁牢固连接，次梁连接在主梁的横向加劲肋上。主梁承受的恒荷载标准值（包括次梁和铺板自重）为 18kN/m2，静力活荷载标准值为 10 kN/m2。钢材为 Q355，焊条为 E50 型、手工焊。试设计主梁。

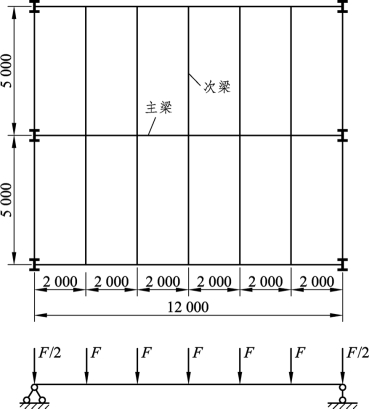
图5.39　例5.4图

【解】 （1）截面尺寸的拟定。

以中间主梁的受力状态作为控制主梁截面的条件。次梁传给主梁的集中荷载：

主梁跨中最大弯矩（不包括自重）：

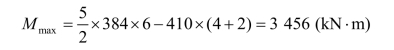
最大剪力：

暂预估：翼缘板厚超过t＞16 mm 、腹板厚度tw＜16 mm ，按f=295 N/mm2、fv=175 N/mm2取值。

需要的截面模量：

① 腹板高度。

最小梁高根据主梁刚度要求（[vT]=l/400）：

经济梁高：

取梁的腹板高度hw=1 200 mm 。

② 腹板厚度。

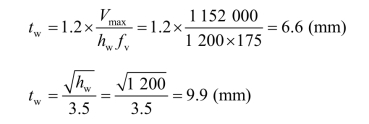
取腹板厚度tw=10 mm 。

③ 翼缘尺寸。

所需翼缘截面面积：

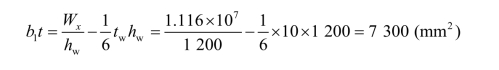
取翼缘宽度b1=400 mm ，厚度t=20 mm。 翼缘板外伸宽度与厚度之比满足局部稳定要求。

拟定截面尺寸如图 5.40 所示。

该截面翼缘厚t=20 mm ＞16 mm ，按f=295 N/mm2取值；腹板厚度tw=10 mm ＜16 mm ，按fv=175 N/mm2取值。

（2）截面验算。

① 内力与截面特性计算。

梁的截面面积：

(www.xing528.com)

梁的自重：

图5.40　拟定截面尺寸（单位：mm）

系数 1.2 为考虑加劲肋及焊缝等重量。

梁跨中最大弯矩：

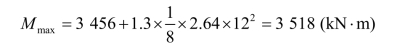
梁的最大剪力：

梁的截面特性（不考虑截面削弱）：

② 梁的强度验算。

a.弯曲应力：

最大弯曲应力满足要求。

b.剪应力：

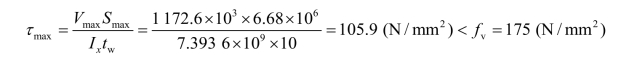
最大剪应力满足要求。

c.折算应力：

跨中截面腹板与翼缘相交处（记为“1”点）：

跨中截面腹板与翼缘相交处折算应力满足要求。

离支座 4 m 处截面腹板与翼缘相交处（记为“2”点）：

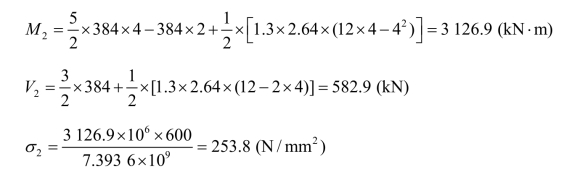
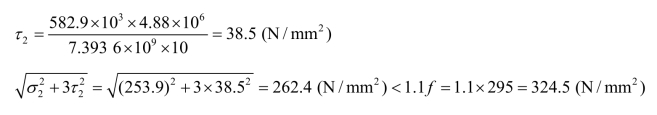
离支座 4 m 处截面腹板与翼缘相交处折算应力满足要求。

综上，梁的强度满足要求。

③ 梁的整体稳定验算。

次梁对主梁有侧向支承作用，主梁受压翼缘的自由长度l1=2 m 。

受压翼缘宽度b1=400 mm ，则：

因此梁的整体稳定可以保证，不必验算。

④ 梁的刚度验算。

集中荷载标准值：

等效均布荷载标准值：

计算挠度时，不考虑因翼缘宽度改变的影响，近似计算。

全部荷载标准值作用：

活荷载标准值作用：

刚度满足要求。

（3）加劲肋设计与局部稳定验算。

梁腹板可考虑屈曲后强度，在支座处和每个次梁处（即固定集中荷载处）设支承加劲肋。端部采用如图 5.41（a）的构造，加横向加劲肋，使a1=500 mm 。

加劲肋板厚t＜16 mm ，取f=305 N/mm2。

① 中间加劲肋。

横向加劲肋截面：

宽度

厚度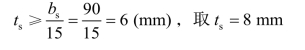

图5.41　主梁加劲肋

中部承受次梁支座反力的支承加劲肋的截面验算：

因　a /h0＞1

故该加劲肋所承受轴心力：

截面面积

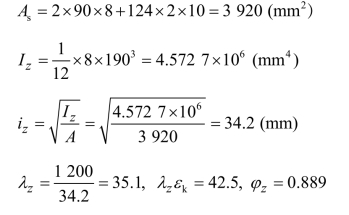
验算加劲肋在腹板平面外稳定：

因为次梁连于主梁的加劲肋上，故不必验算加劲肋端部的承压强度。

② 支座加劲肋。

支座反力R=1 172.6 kN 。

支座加劲肋截面采用-170 ×12，成对对称布置。

验算加劲肋在腹板平面外稳定：

验算端部承压：

支座加劲肋满足要求。

计算支座加劲肋与腹板的连接焊缝：

取hf=6 mm ，则：

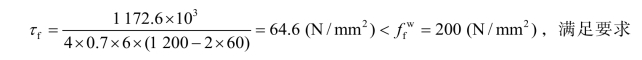
③ 局部稳定计算。

各板块的承载力验算如下。

a.板块Ⅰ

因a1/h0＜1，则：

故τcr=fv，使区格Ⅰ范围内不发生屈曲，支座加劲肋不会受到水平力的作用。

b.板块Ⅱ

左侧截面剪力：V2=1 172.6 -1.3 ×2.64 ×0.5 =1 170.9 (kN)

相应弯矩：　M2=(1 172.6 -384/2)×0.5 -1.3 ×2.64 ×0.52/2 =489.9 (kN ·m)

因M2/Mf＜1，所以应满足V2≤Vu。

因a /t0＞1，则：

c.板块Ⅳ

右侧截面：

因V3＜0.5Vu=755.9 kN ，故应满足M3≤Mcu。

因λb＜0.85，所以ρ=1.0，说明腹板不会发生屈曲，ae=1.0。

M3＜Mcu，满足要求。

另外，梁的整体稳定是能保证的。

（4）梁的变截面设计。

拟采用改变翼缘宽度的方法。

取截面改变处离支座的距离：x =l/6 =12/6 =2 (m)

截面改变处的弯矩：

截面改变处的剪力：

需要的截面模量：

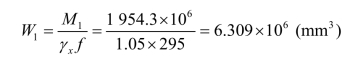
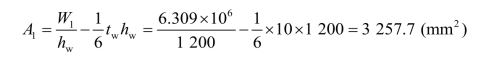
取翼缘宽度为 180 mm，厚度为 20 mm，翼缘面积A1=180 ×20 =3 600 (mm2) ＞3 257.7 (mm2)。

截面改变处强度验算如下。

弯曲应力：

翼缘与腹板相交处（记为“1”点）折算应力：

支座处截面改变后剪应力验算：

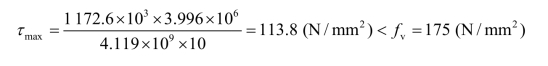
截面改变处强度满足要求。

（5）梁翼缘与腹板的连接焊缝。

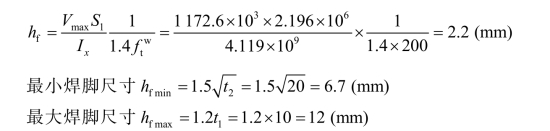
取hf=7 mm 。