组合梁抗弯承载力计算方法

梁腹板在弯矩达到一定程度时受压区出现凸曲变形［图 5.29（a）］。此时若边缘应力未达到屈服点，则梁还能继续承受更大的荷载，但截面上的应力出现重分布，凸曲部分的应力不再继续增大，甚至有所减小，而和翼缘相邻部分及压应力较小和受拉部分的应力继续增加，直至边缘应力达到屈服点。此时梁的中和轴略有下降，腹板受拉区全部有效；受压区一部分退出工作，假定未退出工作的有效截面均匀分布在受压区的上、下部位。所以梁所能承受的弯矩即取有效截面按应力线性分布计算，如图 5.29（c）。

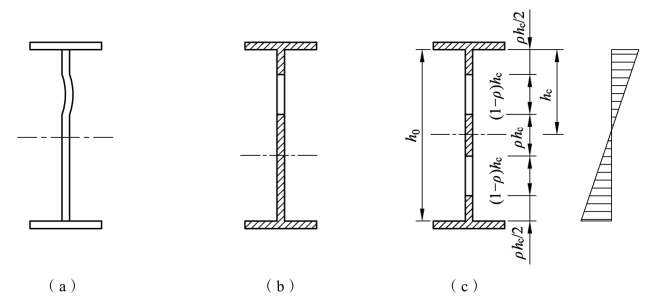
图5.29　弯矩作用时腹板的有效截面

因为腹板屈曲后使梁的抗弯承载力下降不多，在计算梁腹板屈曲后的抗弯承载力时，一般采用近似公式确定。《钢结构设计标准》建议的梁抗弯承载力计算采用有效截面的概念, 假定腹板受压区有效高度为ρhc，等分在hc（hc为腹板受压区高度）的两端，中部则扣去(1-ρ)hc的高度，梁的中和轴下降［图 5.29（b）］。为计算简便，假定腹板受拉区与受压区同样扣去此高度，这样中和轴位置不变［图 5.29（c）］。

梁有效截面惯性矩（忽略孔洞绕本身轴惯性矩）：

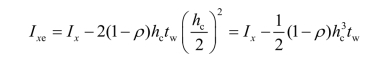
梁截面模量折减系数：

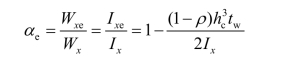
上式是按双轴对称截面、塑性发展系数γx=1.0得出的偏安全的近似公式，也可用于γx=1.05和单轴对称截面的情况。

腹板受压区有效高度系数ρ按下列原则确定：

临界应力公式

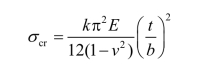
板件受压屈曲后最大受压纤维屈服时

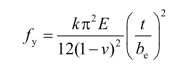
式中　be——板屈服后有效宽度。

由上两式可得：

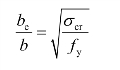(www.xing528.com)

对于受弯的腹板，式左端为而右端则为1/λb，因此：

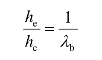
令ρ=he/hc为腹板受压区有效高度系数，考虑到几何缺陷和残余应力等不利影响修正，得：

此式只适用于弹性范围，即适用于λb＞1.25。

当λb≤0.85时，腹板不发生屈曲，即全截面有效，ρ=1.0。

《钢结构设计标准》规定ρ按下列公式计算：

当λb≤0.85时

当0.85＜λb≤1.25时

当λb＞1.25时

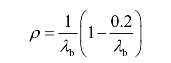
梁的抗弯承载力设计值：

式中的梁截面模量xW按截面全部有效计算。