钢结构梁整体稳定计算

当在最大刚度主平面内单向受弯时，钢梁将发生在弱轴侧向的弯扭失稳。当梁截面最大受压纤维弯曲压应力不超过整体稳定的临界应力，表示梁能保持整体稳定。考虑抗力分项系数Rγ后，钢梁的整体稳定计算公式为：

或写成《钢结构设计标准》采用的形式：

式中Mx——绕截面强轴x作用的最大弯矩设计值；

Wx——按受压最大纤维确定的梁毛截面抵抗矩：当截面板件宽厚比等级为S1、S2、S3或S4级时，应取全截面模量；当截面板件宽厚比等级为S5级时，应取有效截面模量；

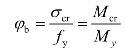——梁整体稳定系数，My为受压边缘纤维屈服弯矩。

当钢梁双向受弯时，钢梁仍将发生在弱轴侧向的弯扭失稳，其整体稳定计算采用以下公式：

式中Mx，My——按受压纤维确定的对x轴（强轴）和对y轴的毛截面模量；

φb——绕强轴弯曲所确定的梁整体稳定系数。

式（5.20）为一经验公式，式中第二项表示绕弱轴弯曲的影响，但分母中γy在此处仅起适当降低引项影响的作用，并不表示截面允许发展塑性。

1．弹性失稳

当钢梁的受压翼缘宽度1b较小（即侧向刚度小），同时侧向支承点间的自由长度l1又较大时，σcr常小于钢材的屈服强度fy，即钢梁失稳时材料处于弹性阶段。《钢结构设计标准》取

代入数值E=206 ×103 N/mm2,E /G=2.6，即得到稳定系数的近似值。

双轴对称工字形截面简支梁受纯弯曲时：

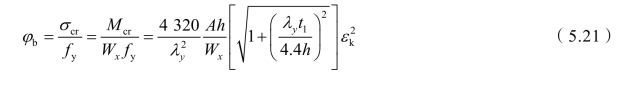
实际工程中梁受纯弯曲的情况很少，通常梁会受横向荷载作用，此时，临界弯矩的理论值应按式（5.18）计算，再求得相应的稳定系数φb。但这样计算非常复杂，所以通过选取较多的常用截面尺寸，进行计算机分析，得出了不同荷载作用下的稳定系数与纯弯曲作用下稳定系数的比值βb；同时为了能适用于单轴对称焊接工字形或轧制H型钢简支梁的一般情况，整体稳定系数φb的计算公式变为：

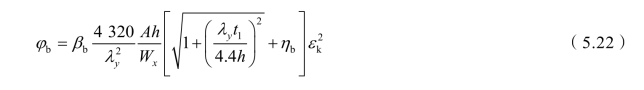
式中　A，Wx——截面毛截面面积和按最大压应力确定的毛截面模量；

h，t1——截面高度和受压翼缘厚度；

λy——工字钢梁绕弱轴的长细比，λy=l1/iy，l1为梁侧向梁曲时的自由长度；

βb——梁整体稳定的等效弯矩系数，是不同荷载作用时梁的临界弯矩Mcr或φb与同等条件下梁受纯弯曲时的Mcr或φb的比值，通过该系数可以把非纯弯曲荷载等效为纯弯曲荷载，以便引用纯弯曲荷载作用的稳定计算公式；

ηb——截面不对称影响系数：双轴对称工字形截面bη=0；对单轴对称工字形截面，当加强受压翼缘时ηb=0.8(2αb-1)＞0，当加强受拉翼缘时ηb=2αb-1 ＜0；αb=I1/(I1+I2)，I1、I2分别是受压翼缘和受拉翼缘对 y 轴的惯性矩。

上述所有物理量，都只随梁的侧向无支承长度和截面的形状、尺寸等变化，可根据所给数据直接计算，与荷载无关。与荷载有关的只是梁整体稳定的等效弯矩系数βb，H 型钢和等截面工字形简支梁的bβ按表 5.5 取值。

表5.5　H型钢和等截面工字形简支梁的等效弯矩系数bβ

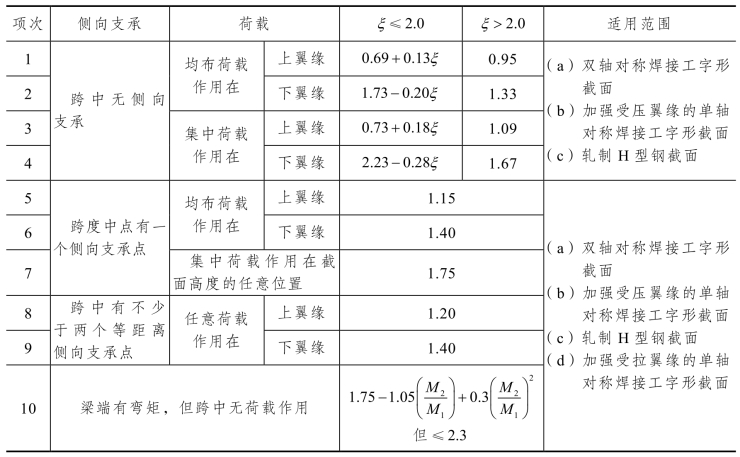
注：1.ξ为参数，其中b1为受压翼缘的宽度。
2.M1和M2为梁的端弯矩，使梁产生同向曲率时M1和M2取同号，产生反向曲率时取异号，
3.表中项次3、4和7的集中荷载是指一个或少数几个集中荷载位于跨中央附近的情况，对其他情况的集中荷载，应按表中项次1、2、5、6内的数值采用。
4.表中项次8、9的βb，当集中荷载作用在侧向支承点处时，取βb=1.22。
5.荷载作用在上翼缘系指荷载作用点在翼缘表面，方向指向截面形心；荷载作用在翼缘下缘系指荷载作用点在翼缘表面，方向背向截面形心。
6.对αb＞0.8的加强受压翼缘工字形截面，下列情况的βb值应乘以相应的系数：

项次1：当ξ≤1.0时，乘以0.95。

项次3：当ξ≤0.5时，乘以0.90；当0.5＜ξ≤1.0时，乘以0.95。

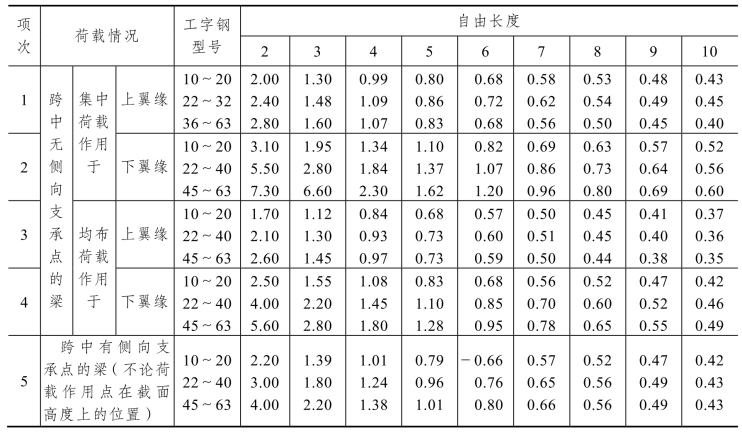
对于轧制普通工字钢，截面虽然属于双轴对称截面，但其翼缘厚度是变化的，不能把翼缘板简化为矩形截面。此外，轧制普通工字钢的翼缘内侧有斜坡，翼缘板与腹板交接处具有加厚的圆角。其φb如果简单套用焊接工字形截面简支梁的φb公式求取，将引起较大的误差。为此《钢结构设计标准》中对轧制普通工字钢简支梁的φb直接给出了轧制普通工字钢简支梁的bφ表（如表 5.6 所示），可按荷载情况、工字钢型号，由侧向支撑点间的自由长度l1直接查对应的稳定系数。

表5.6　轧制普通工字钢简支梁的稳定系数bφ

对于轧制槽钢简支梁，按纯弯曲情况偏安全地按式（5.23）计算其稳定系数。

(www.xing528.com)

式中　h，b，t——槽钢截面的高度、翼缘宽度和平均厚度。

2．弹塑性失稳

若钢梁失稳发生在钢材发展塑性的弹塑性阶段，意味着部分截面应力已达到屈服点，并形成塑性变形区，对继续抵抗弯曲和扭转变形已不再起作用，此时的稳定承载能力必定比按弹性材料计算有显著降低。因此规范规定：按前述的弹性失稳计算得到的bφ＞0.6时，表明梁的整体失稳必定发生在弹塑性阶段，应对bφ进行修正，采用修正后的整体稳定系数bφ′计算梁的整体稳定。

因为梁丧失整体稳定时必然同时发生侧向弯曲和扭转变形，如果构造上能有效防止梁侧弯则可保证其不发生整体失稳。规范规定当符合以下情况之一的钢梁可不计算其整体稳定：

（1）当梁上有铺板（钢筋混凝土板和钢板）密铺在梁的受压翼缘上并与其牢固相连，能阻止梁受压翼缘的侧向位移时。

（2）H 型钢和工字形等截面简支梁受压翼缘的自由长度与其宽度之比不超过表5.7 所列数值时。

（3）箱形截面简支梁的截面（如图 5.18 所示）高宽比

表5.7　H型钢或工字形等截面简支梁不需计算整体稳定的最大11/l b值

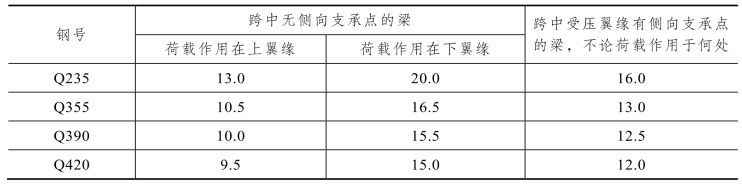
注：1.其他钢号不需要计算整体稳定性的最大11/l b值，应取Q235钢的数值乘以钢号修正系数εk。
2.表中对跨中无侧向支承点的梁，l1为其跨度；对跨中有侧向支承点的梁，l1为受压翼缘侧向支承点间的距离（梁的支座处视为有侧向支承）。b1为受压翼缘板的宽度。

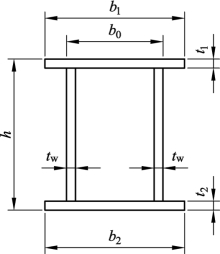
图5.18　箱形截面尺寸示意图

【例5.2】 某工作平台简支纵梁，跨径 5 m，采用 Q235B 钢材，截面为型钢HN350×175×7×11，纵梁两端连接在横梁加劲肋上，纵梁之上是铺板，但铺板与纵梁不刚性连接。纵梁恒载（含自重）标准值 5 kN/m，活荷载 20 kN/m。试检算该纵梁。

【解】 纵梁承受的荷载标准值为：

荷载设计值为可变荷载效应控制的组合：恒荷载分项系数为 1.3，活荷载分项系数为 1.5。即：

纵梁最大弯矩设计值为：

型钢 HN350×175×7×11的截面特性值：A=6 366 mm2, Ix=1.37×108 mm4, Wx=7.82 ×105 mm3，iy=39.3 mm 。

对于型钢，腹板较厚，一般不必检算抗剪强度；同时纵梁连接于主梁加劲肋上，也不必检算其局部承压强度。

纵梁上铺板与纵梁不连接，且纵梁受压翼缘的自由长度与其宽度之比5 000/175＝28.6 ＞ 13.0，需要检算其整体稳定。

对于跨中无侧向支承的梁，均布荷载作用于上翼缘时：

检算整体稳定：

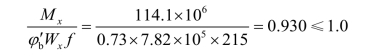
梁的整体稳定满足要求。

截面无削弱，故可不检算弯曲正应力强度。

检算挠度：

在全部荷载标准值作用下

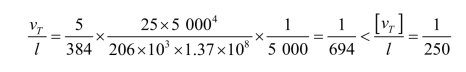
在可变荷载标准值作用下

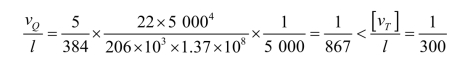
荷载作用下梁的挠度满足要求。