假如由材料力学的剪应力计算公式τ=VS /Itw可求得梁截面的竖向剪应力,如图 5.13(a)所示。此公式对钢梁薄壁构件则存在不合理的地方。例如:对工字形截面梁,以此公式计算的腹板剪应力顺着腹板中轴线方向是合理的;但对翼缘,在翼缘与腹板的交接处发生翼缘剪应力很小而腹板剪应力较大的剧烈突变,这不合理。这是由于计算翼缘剪应力时假定剪应力沿翼缘全宽均匀分布,实际上,翼缘内外表面[如图 5.13(a)中所示的cd和ef段及ab段]为自由表面,不存在水平剪应力,因而翼缘截面上也不会有图中所示的垂直于这些自由表面方向的竖向剪应力,故剪应力沿翼缘全宽均匀分布的假定规律就是错误的。
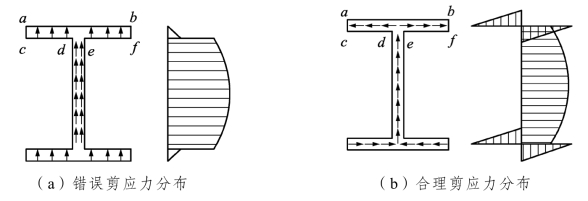
图5.13 工字形截面剪应力分布图
工字形截面上的实际剪应力分布应如图 5.13(b)所示的剪力流:截面各点剪应力均为顺着薄壁截面的中轴线方向,在与之垂直即壁厚方向的剪应力则很小,可忽略不计;且由于壁薄,可假定剪应力沿厚度方向均匀分布。
由对称关系可知,对于双轴对称截面的梁,如工字形截面梁,梁横向荷载作用在形心轴上时,梁只产生弯曲,不产生扭转。这时,截面上三角形分布的弯曲应力的合力等于弯矩 M,截面上剪力流的合力是通过形心轴的剪力 V,正好平衡。
但对于槽形、T形、L形等非双轴对称截面,当横向荷载作用在形心轴的非对称轴上时,梁除产生弯曲外,还伴随有扭转。(https://www.xing528.com)
如图 5.14 所示的槽形截面梁,截面上存在某一特殊点 S,当横向荷载P通过S点时,截面上腹板剪应力合力V、上翼缘的剪应力合力yV和下翼缘的剪应力合力yV对S点合力矩为零,因此截面能维持面内的力矩平衡。也就意味着P作用下梁截面上只会发生弯曲变形。但当横向荷载P不通过S点,而是通过O点时,各剪应力合力对 O 点力矩肯定不为零,必然,截面上将产生扭矩才能维持面内平衡。也就是说,梁此时不仅会发生弯曲变形,还会因为扭矩的存在而发生扭转变形。此 S 点称为截面的扭转中心或剪切中心。

图5.14 槽形截面受剪时的截面内力
如图 5.15 所示,剪切中心 S 的位置一般有如下简单规律:① 有对称轴的截面,S 在对称轴上;② 双轴对称截面和点对称截面(如 Z 形截面),S 与截面形心重合;③ 由矩形薄板相交于一点组成的截面,S 在交点处。

图5.15 常见截面的剪切中心S示意图
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




