5.2.4折算应力在变截面工字形组合截面简支梁中的应用

在组合梁的腹板计算高度边缘处，当同时受有较大的正应力、剪应力和局部压应力时，或同时受有较大的正应力和剪应力时，应根据第四强度理论计算该点位处的折算应力：

式中　σ——计算点位处（腹板计算高度边缘）的弯曲正应力，按弹性计算，不考虑塑性深入截面；

σc——计算点位处（腹板计算高度边缘）的局部承压应力，与弯曲正应力的方向相垂直；

τ——计算点位处（腹板计算高度边缘）的剪应力。

需要注意的是，公式（5.8）中的σ、σc、τ分别为腹板计算高度边缘同一点上同时产生的正应力、局部压应力和剪应力。σ和cσ以拉应力为正值，压应力为负值。考虑到需要验算折算应力的部分只是梁的局部区域，几种应力皆以其较大值在同一点上出现的概率很小，因而引入大于1的强度增大系数1β。由于当σ与cσ异号时，其塑性变形能力较σ与cσ同号时要高，因此规定1β的取值原则为：

当σ与σc异号时，β1=1.2；

当σ与σc同号或σc=0时，β1=1.1。

对于同时受弯和受剪截面处，弯曲正应力和剪应力都较大的点位，可能为不利点，应计算其折算应力。如图 5.10 所示的变截面工字形组合截面简支梁在均布荷载和两个集中荷载作用下，只有 a、b 两处截面需要进行折算应力的计算，且截面上的计算点位是腹板与翼缘板相接处。

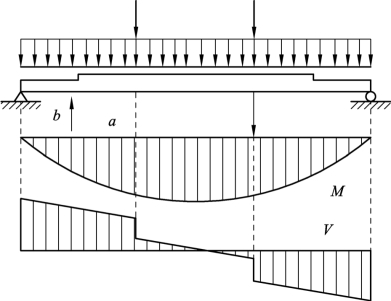
图5.10　折算应力计算截面

【例 5.1】 如图 5.11 所示焊接工字形截面框架主梁跨度 4 m，两端与柱铰接，主梁跨中顶面作用有集中荷载，其设计值为P=220 kN ，集中荷载的支承长度a=80 mm，主梁截面如图所示。钢材为 Q235B，f=215 N/mm2。如忽略梁自重，试验算主梁的强度。

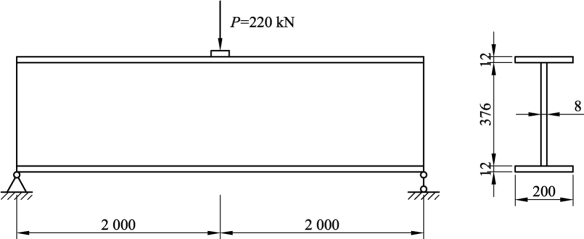
图5.11　例5.1图（单位：mm）

【解】 梁跨中弯矩最大，最大弯矩设计值：

梁支座及跨中附近剪力最大，最大剪力设计值：

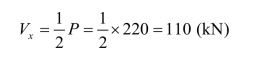
梁截面几何参数：

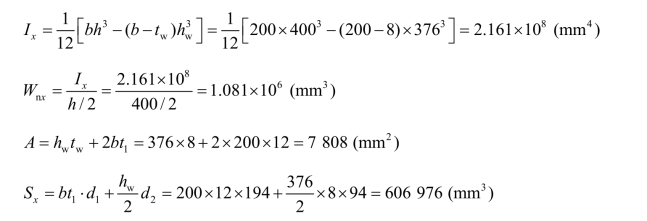(www.xing528.com)

（1）验算抗弯强度。

对于简支梁，由于翼缘截面板件的宽厚比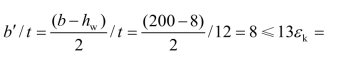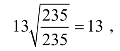可按弹塑性进行设计，取截面发展系数γx=1.05。

梁抗弯强度满足要求。

（2）验算抗剪强度。

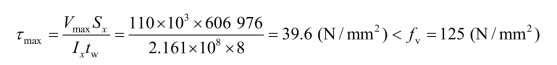
梁抗剪强度满足要求。

（3）验算局部承压强度。

因主梁跨中顶面作用有集中荷载，且无支承加劲肋，所以需验算局部承压强度。

由题可知支承长a=80 mm ，腹板与翼缘交接处（记为“1”点）局部承压强度最大：

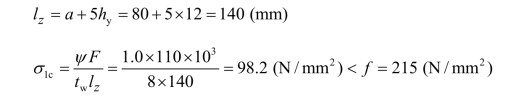
梁局部承压强度满足要求。

（4）验算折算应力。

集中荷载作用位置处截面的弯矩、剪力均为最大，该截面的腹板与翼缘相交处的弯矩和剪力此时都相对较大，该点位（“1”点）为可能的危险点，因而需验算该点位处折算应力。

腹板与翼缘相交处：

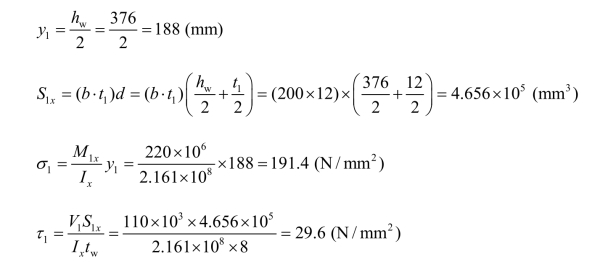
因σ1与τ1同号，β1=1.1，则：

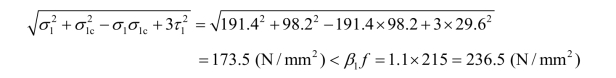
梁折算应力最危险点满足要求。

综上，该梁的最大弯曲正应力、最大剪应力、局部承压应力以及可能危险点位处折算应力均满足要求。