轴心受压构件的扭转屈曲和弯扭屈曲原理

构件失稳按形态分为：弯曲失稳、扭转失稳、弯扭失稳。轴心受力构件，轴压力必须通过截面形心，若截面剪切中心（也称剪心）与形心不重合，压力不通过截面剪切中心，构件可能会发生弯扭屈曲。单轴对称截面受压柱，将发生的变形（失稳形态）之一，是绕对称轴的弯曲+扭转=弯扭。形心与剪心不重合的截面可能会发生弯扭屈曲，形心与剪心重合（双轴对称截面），只会发生弯曲失稳或者扭转失稳。截面形心 O 与剪切中心 S 如图 4.43 所示。

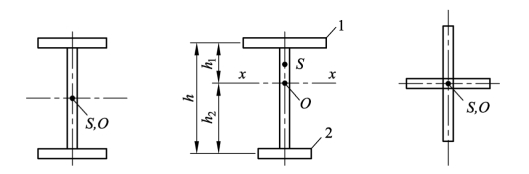
图4.43　截面形心 O 和剪切中心 S

1．用换算长细比计算弯扭失稳和扭转失稳

弯曲屈曲理论较为成熟，稳定系数φ值包含了初始缺陷的不利影响，弯扭屈曲、扭转屈曲的分析比弯曲屈曲复杂，理论也不如弯曲屈曲成熟。目前的普遍做法是，把按弹性稳定理论算得的弯扭屈曲临界力换算成为长细比较大的弯曲屈曲杆件，即按弹性稳定理论解出的弯扭或扭转屈曲临界力与弯曲屈曲临界力的公式相等，解出相应的“换算长细比”，再按换算长细比从规范表格中查得相应的弯曲失稳稳定系数。用换算长细比按弯曲失稳计算，虽然换算是按弹性考虑进行，但由于弯曲屈曲中考虑了非弹性和初始缺陷，这就相当于弯扭屈曲也间接考虑了非弹性和初始缺陷的影响。这种做法意味着把初始几何缺陷和残余应力的效应看成和弯曲屈曲完全一致，实际上不会恰好如此。虽然理论上并不十分严密，但此法是当前工程界普遍认同的方法。

弯曲屈曲、弯扭屈曲、扭转屈曲，对截面形状和长细比要求是不同的。弯曲屈曲控制设计，宜采用薄壁构件；扭转屈曲、弯扭屈曲控制设计，板件宽厚比过大未必有利。因为弯曲屈曲理论较为成熟，所以可通过适当加大长细比，使弯曲屈曲控制设计。

弯曲计算，会用到截面对形心主轴的惯性矩Ix、Iy和抗弯刚度EIx、EIy，这些指标在弯扭屈曲、扭转屈曲计算中也要用到。此外，弯扭屈曲、扭转屈曲计算中还要用到如下几何特性：剪切中心 S、抗扭惯性矩tI（也称扭转常数）、扇形惯性矩Iω（也称翘曲常数）。这些几何特性可以参阅弹性稳定理论相关书籍，以下列举常用到的一些简单情形。

1）剪切中心 S

（1）双轴对称截面剪切中心与截面形心重合。

（2）开口薄壁构件若有对称轴，剪切中心位于对称轴上。

（3）单轴对称工字形截面，剪切中心不与形心重合，位于对称轴接近较大翼缘一侧。

（4）槽钢截面剪切中心位于腹板外侧的对称轴上。

（5）十字形截面、角钢截面、T形截面，剪切中心位于组成截面的狭长形矩形截面中心线的唯一交点。

2）抗扭惯性矩It

横截面不是圆形（实心或空心）的构件，发生扭转时，横截面不再保持为平面而发生翘曲，截面翘曲受到约束的扭转称为约束扭转。扭转过程中，截面能“自由翘曲”的扭转称为自由扭转。抗扭惯性矩It为自由扭转时的截面特性，It可查阅相应手册。对开口薄壁构件，也可以将横截面形状表示为若干矩形的组合。偏安全地按下式计算其抗扭惯性矩：

式中，bi、ti为组成截面各矩形的宽度和厚度。

3）扇形惯性矩Iω

扇形惯性矩Iω是开口薄壁构件在约束扭转时的截面特性，与抗弯刚度EI、抗扭刚度GIt相对应，EIω是构件的翘曲刚度。

（1）十字形截面、T 形截面、角钢截面可取：

（2）单轴对称工字形截面：

式中：I1、I2为工字形截面较大翼缘和较小翼缘对截面对称轴 y 的惯性矩（显然，I1+I2=Iy）；h为上下翼缘板形心间的距离。

（3）双轴对称工字形截面：

公式（4.15）均为近似公式，准确的公式、其他截面扭转惯性矩、扇形惯性矩计算公式，可查阅相应手册。

4）扭转失稳

按弹性稳定理论，扭转失稳时，临界力计算公式为：

式中　I0，It，Iω——构件毛截面对剪心的极惯性矩（mm4，I0=Ix+Iy）、抗扭惯性矩（mm4）和扇性惯性矩（mm6），对十字形截面可近似取0Iω=；lω——扭转屈曲的计算长度：两端铰支且端截面可自由翘曲者，取几何长度 l；两端嵌固且端部截面的翘曲完全受到约束者，取0.5l；

E，G ——弹性模量和剪变弹性模量。

设λz为扭转失稳换算长细比，令扭转失稳临界力与弯曲失稳欧拉公式相等：

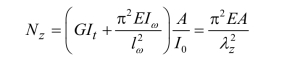
将E =206 ×103N/mm2,G=79 ×103N/mm2代入上式解出扭转失稳“换算长细比”：

由λz/εk查出稳定系数φ，从而得到构件扭转屈曲最大承载力Nu=φfA。

注意，加大构件长细比λ，弯曲失稳临界力减小，但扭转失稳临界力与构件长细比λ无关，所以可采用较大的长细比，使弯曲失稳控制设计。

例如，对十字形截面如图 4.44，抗扭惯性矩为十字形截面，Iω很小，取I0ω=，所以

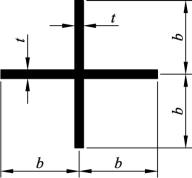
图4.44　十字形截面扭转常数计算

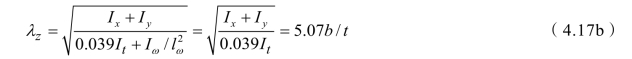
此值与构件长度无关，原钢结构设计规范要求λx≥5.07b /t 和λy≥5.07b /t，就不会发生扭转失稳，设计由弯曲失稳控制，这正是希望的。扭转失稳临界力与柱长无关，长细比大的构件发生弯曲失稳。

GB 50017—2017 标准将上述规定简化为b /t≤15εk→可不计算扭转屈曲，原因如下。

将十字形截面Iω≈0，代入扭转临界力公式：

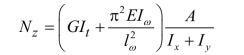
得十字形截面扭转失稳临界力为：

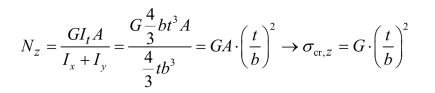
若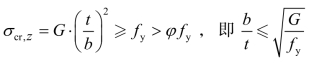时，弯曲屈曲控制设计，将钢号修正系数得到：

由弯曲屈曲控制设计（不会发生扭转屈曲）。

设计标准取：

满足公式（4.18），扭转失稳承载力大于弯曲失稳承载力，只需要按照弯曲失稳计算，不必计算扭转失稳。

5）弯扭失稳

按弹性稳定理论，单轴对称截面轴心受压构件绕对称轴y弯扭屈曲的临界力可由下列方程求得：

式中Nyz——构件弯扭失稳临界力；

Ny——对y轴的欧拉临界力，

Nz——扭转屈曲的临界力，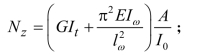

ys——截面剪切中心到形心的距离；

i0——截面对剪切中心的极回转半径，

解二次方程［公式（4.19）］，得到的最小根即为弯扭屈曲的临界力Nyz。

为简化计算，设λyz为弯扭失稳换算长细比，将代入公式（4.19），可解出构件弯扭失稳换算长细比为：

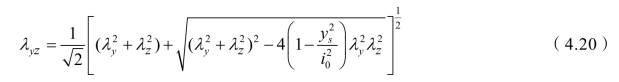
式中λz——扭转屈曲换算长细比，由式（4.17）确定。

2．换算长细比的简化计算公式

单角钢截面、双角钢组合截面构件绕对称轴弯扭屈曲的换算长细比可用《钢结构设计标准》（GB 50017—2017）给出的下列简化公式计算。

1）单角钢截面

（1）等边角钢

计算分析和试验都表明，等边单角钢轴压构件当两端铰支且没有中间支点时，绕强轴（u 轴）弯扭屈曲的承载力总是高于绕弱轴弯曲屈曲承载力，因此条文明确指出这类构件无须计算弯扭屈曲。

（2）不等边角钢（图4.45）

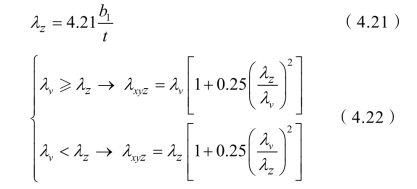
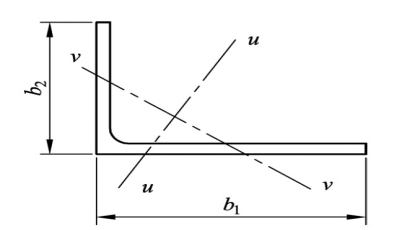
图4.45　不等边角钢

（3）单边连接的单角钢

一边与节点板相连的单角钢轴心受压构件，可不计算弯扭失稳，但应考虑偏心受力的不利影响按下式计算整体稳定：

式中：λ为长细比，对中间无横向联系的单角钢压杆，按最小回转半径计算；当λ＜20，取λ=20（注意，此处关于λ的规定，仅用于计算η，φ值计算所用的长细比，仍然按计算轴压构件整体稳定的相关规定采用）。

2）双角钢组合T形截面（图4.46）

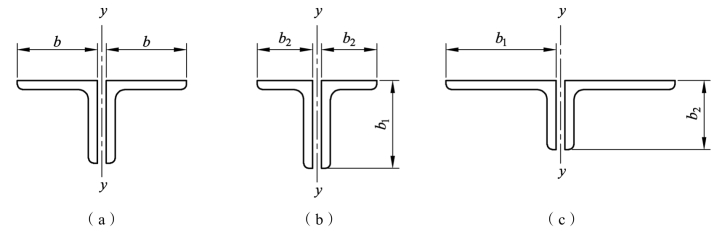
图4.46　双角钢组合T形截面

（1）等边双角钢

（2）短肢相并的不等边双角钢

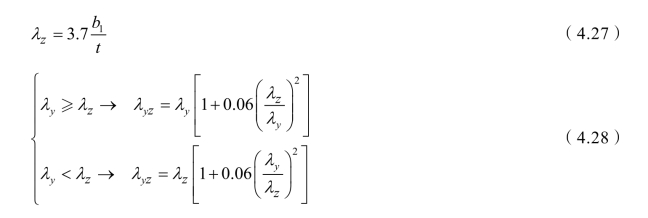
（3）长肢相并的不等边双角钢

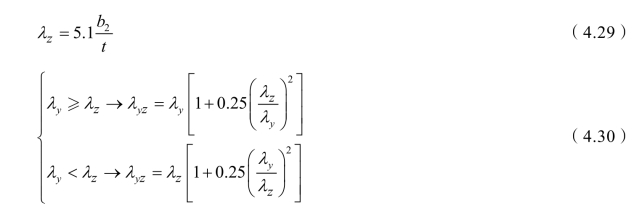
3．美国规范（ANSI/AISC 360-16）对弯扭、扭转屈曲的计算

以下介绍ANSI/AISC 360-16规范对弯扭屈曲的计算，作为与中国规范计算的比较。下列计算弯扭屈曲公式中，弹性模量E=2 ×105 N/mm2，φ=0.9为承载力折减系数，lω为扭转屈曲的计算长度。(www.xing528.com)

非薄柔型板件（即欧洲、美国规范的Ⅰ、Ⅱ、Ⅲ类板件，中国规范的S1、S2、S3、S4类板件）组成的构件的扭转和弯扭屈曲计算：

单角钢必须符合：

弯扭屈曲承载力：

Pn由弯曲屈曲公式（4.14）计算，但σcr式中的σe由下式计算。

（1）对于绕剪切中心扭转的双对称构件：

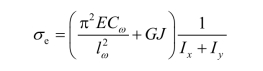
（2）对于绕剪切中心扭转的单对称构件（y轴为对称轴）：

若 x 为对称轴，用Fex代替Fey。

式中　Cω——翘曲常数：

对双轴对称工字形截面取Cω=代替更精确的分析，h0为上下翼缘形心间的距离。

对于T形及双角钢截面，计算σez时，取Cω=0，x0=0。

G——剪切模量，G=77 200 N/mm2。

J——扭转常数。

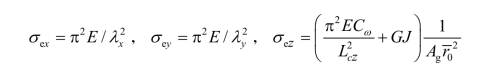
弯曲常数

其中　x0，y0——剪切中心相对于形心的坐标。

【例4.12】 两端铰接轴心受压构件，构件长度l=6 m ，无侧向支撑，端部截面可自由翘曲，截面尺寸如图 4.47 所示。采用Q235钢。试确定：

（1）此柱承载力由弯曲屈曲还是扭转屈曲决定。

（2）柱所能承担的轴心压力设计值Nu。

【解】 应该先行验算板件宽厚比符合局部稳定的要求。

图4.47　例4.12图

→绕弱轴弯曲失稳控制设计

柱所能承担的轴心压力设计值为：

弯曲失稳控制。

【例 4.12续】 在长度中点处有垂直于y轴的侧向支撑，确定此柱承载力由弯曲屈曲还是扭转屈曲决定，并求出柱所能承担的轴心压力设计值uN。

【解】（1）若此支撑仅支于截面剪心（图 4.48 左图），支撑点能阻止构件对y轴的弯曲，不能阻止扭转，扭转屈曲换算长细比仍为λω=75.3(λω=79.1)，弯曲长细比λy=300/6.27 =47.8＜λω，由扭转失稳控制设计（不希望如此）。

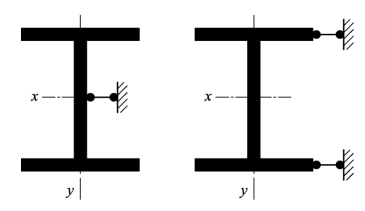
图4.48　例4.12续图

（2）若长度中点的支承既能阻止杆件侧移，又能阻止其扭转（图4.48 右图），则：

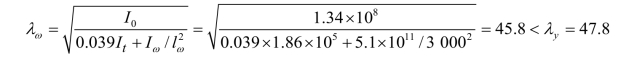
绕弱轴弯曲失稳控制设计。

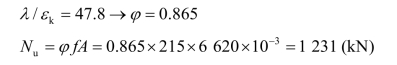
一般，工字形和箱形截面轴压构件，抗扭刚度较大，扭转屈曲临界力大于弯曲屈曲临界力，设计由弯曲控制，这是所希望的。但侧向支承约束弯曲屈曲、未约束扭转屈曲，则有可能扭转屈曲控制设计。

【例4.13】 两根轴心受压构件，构件A为双角钢2 ∠160 ×10组成的T形截面，构件B为双角钢2 ∠100 ×16组成的T形截面，角钢连接在节点板上，节点板厚度 10 mm，构件两端铰接，构件长度l=2 m 。采用Q235钢。

求两根构件所能承受的最大轴心压力设计值。

【解】（1）查型钢规格表并计算得到相应数据。

（2）计算2 ∠160 ×10。

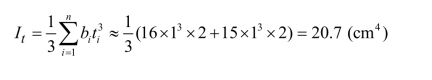
绕对称主轴的弯扭屈曲时，长细比应按下式确定：

若按美国ANSI/AISC 360-16规范，Nu=936.3 kN（弯扭屈曲控制设计）。

（3）计算2 ∠100 ×16。

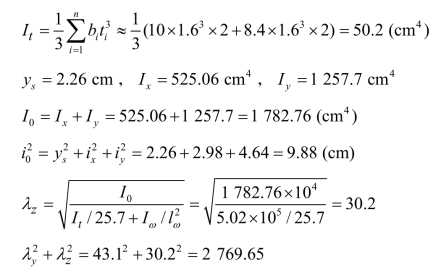
绕对称主轴的弯扭屈曲时，长细比应按下式确定：

若按美国ANSI/AISC 360-16规范，Nu=1 001 kN （弯曲屈曲控制设计）。

（4）按GB 50017—2017 推荐的简化公式计算。

① 2 ∠160 ×10：

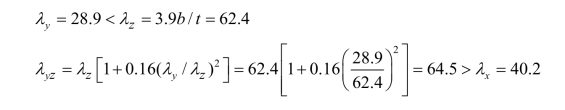
弯扭屈曲确定承载力：

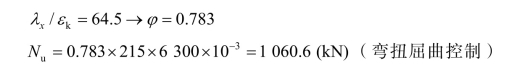
② 2 ∠100 ×16：

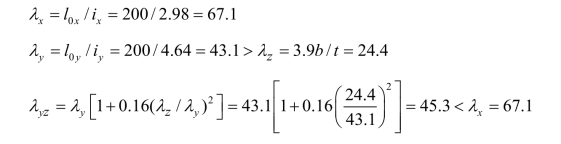
弯曲屈曲确定承载力：

可见，设计标准简化公式计算简便，结果相差很小。

（5）改变构件长度，采用标准推荐的简化计算可得：

① 若构件长度l=1m：

2 ∠160 ×10　Nu=1 072 kN（弯扭屈曲控制设计）

2 ∠100 ×16　Nu=1 250 kN（弯曲屈曲控制设计）

② 若构件长度l=3 m：

2 ∠160 ×10　Nu=1 039 kN（弯扭屈曲控制设计）

2 ∠100 ×16　Nu=700.6 kN（弯曲屈曲控制设计）

可通过不同构件长度承载力，形成图 4.49，该图说明：柱长 2 m，截面面积几乎相同的两种角钢承载力几乎一样；构件长度l＞2 m ，由弯曲屈曲控制设计，宜采用薄而宽的角钢截面；构件长度l＜2 m ，由弯扭屈曲控制设计，宜采用厚而窄的角钢截面。弯曲屈曲，在满足板件宽厚比前提下，选择薄而宽的截面，使截面尽量远离形心轴，有助于面积不变的前提下增大惯性矩，提高承载力。扭转、弯扭屈曲，选择薄而宽的截面未必有利。

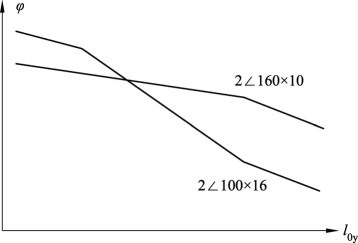
图4.49　角钢肢宽厚比对承载力的影响

图 4.50 为典型槽钢在弯曲、扭转和弯扭模式下的屈曲曲线：λ较小时（短柱），发生绕对称轴（y 轴）的弯扭失稳（临界力为Ncr,yz）；λ较大时（长柱），发生绕非对称轴（x轴）的弯曲失稳（临界力为Ncr,x）。和十字形截面一样，为了使弯曲失稳控制设计，设计时可适当加大构件长细比。图中Ncr,T为扭转屈曲临界力，不控制设计。

图4.50　典型槽钢在弯曲、扭转和弯扭模式下的屈曲曲线

【例 4.14】 图 4.51 所示单边连接在节点板上的某钢屋架竖腹杆，采用单角钢∠56 ×4，Q235钢材，截面无削弱，构件长度l=106 cm ，构件计算长度l0u=l0v=l0=95.4 cm 。计算该构件所能承受的最大轴心压力设计值uN。

【解】 设计标准规定，等边单角钢轴压构件当两端铰支且没有中间支点时，绕强轴（u 轴）弯扭屈曲的承载力总是高于绕弱轴弯曲屈曲承载力，无须计算弯扭屈曲，但一边与节点板相连的单角钢轴心受压构件，应考虑偏心受力的不利影响按公式（4.23）、（4.24）计算整体稳定。

角钢∠56 ×4截面特性数据：

图4.51　例4.14图

由绕截面最小刚度轴v控制整体稳定：

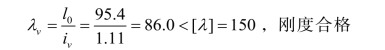
查表φv=0.648，则：

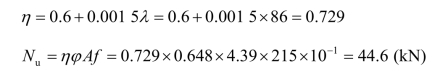
局部稳定验算参见后面的例题。