直角角焊缝计算-钢结构设计原理

1．直角角焊缝强度计算的基本公式

试验表明直角角焊缝的破坏面通常发生在 45° 方向的最小截面，此截面称为直角角焊缝的有效截面或计算截面。在外力作用下，直角角焊缝有效截面上产生3 个方向应力，即σ⊥、τ⊥、//τ（图 3.33）。3 个方向应力与焊缝强度间的关系，根据试验研究，可用式（3.11）表示：

式中　σ⊥——垂直于角焊缝有效截面上的正应力；

τ⊥——有效截面上垂直于焊缝长度方向的切应力；

τ//——有效截面上平行于焊缝长度方向的切应力；

——角焊缝的强度设计值。

以图3.33（c）所示受斜向轴心力N（互相垂直的分力 Ny和 Nx）作用的直角角焊缝为例，来说明角焊缝基本公式的推导。Ny在焊缝有效截面引起垂直于焊缝一个直角边的应力fσ，该应力对有效截面来说既不是正应力，也不是切应力，而是σ⊥和τ⊥的合应力。

图3.33　焊缝有效截面上的应力

式中　Ny——垂直于焊缝长度方向的轴心力；

he——直角角焊缝的有效厚度，he＝0.7hf；

lw——焊缝的计算长度，考虑起灭弧缺陷，按各条焊缝的实际长度，每端减去hf计算，对每条焊缝计算长度取其实际长度减去 2hf。

由图 3.33（c）知，对直角角焊缝：

沿焊缝长度方向的分力Nx在焊缝有效截面引起平行于焊缝长度方向的切应力τf=τ//，则

则可得直角角焊缝在各种应力综合作用下，fσ和fτ共同作用处的计算式为：

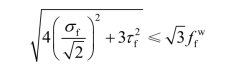
令则：

式中　βf——正面角焊缝的强度增大系数：对承受静力荷载和间接承受动力荷载的结构，；对直接承受动力荷载的结构，βf=1。

对正面角焊缝，此时τf=0，得：

对侧面角焊缝，此时σf=0，得：

式（3.15）～式（3.17）即为角焊缝的基本计算公式。只要将焊缝应力分解为垂直于焊缝长度方向的应力σf和平行于焊缝长度方向的应力τf，上述基本公式就可适用于任何受力状态。应注意的是公式中σf、τf仅表示简化计算中和焊缝长度方向的垂直与平行方向，与力学中的正应力、剪应力概念不同。

角焊缝的强度与熔深有关。埋弧自动焊熔深较大，若在确定焊缝有效厚度时考虑熔深，焊缝有效厚度将增大，提高了角焊缝的承载能力，可带来较大的经济效益。我国规范不分手工焊和埋弧焊，均统一取有效厚度 he＝0.7hf，对自动焊来说偏保守。

对于斜角角焊缝，其受力复杂，一般仍按式（3.15）～式（3.17）计算，但偏保守地取f1β=。角焊缝连接在以下几种常见受力情况下的计算方法分别叙述如下。

2．轴心力作用的角焊缝连接计算

1）采用盖板的角焊缝连接计算

当轴心力通过连接焊缝中心时，可认为焊缝应力是均匀分布的。在图3.34的连接中，当只有侧面角焊缝时，按式（3.17）计算；当只有正面角焊缝时，按式（3.16）计算。

图3.34　受轴心力的盖板连接

当采用三面围焊时，先按式（3.16）计算正面角焊缝所承当的内力：

式中　——连接一侧正面角焊缝有效面积的总和。

再由式（3.17）计算侧面角焊缝的强度：

式中——连接一侧侧面角焊缝有效面积的总和。

2）斜向轴心力作用下角焊缝的计算

如图 3.35 所示，通过焊缝重心作用一轴向力 F，轴向力与焊缝长度方向夹角为θ。

图3.35　斜向轴心力作用

将力 F 分解为垂直和平行于焊缝长度方向的分力N =F sin θ，V =Fcosθ ，则：

将式（3.20）和式（3.21）代入式（3.15）中，得：

取，得：

令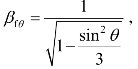则斜焊缝的计算公式为：

式中　βfθ——斜焊缝的强度增大系数，其值介于 1.0～1.22，对直接承受动力荷载的结构βfθ=1；

θ——作用力与焊缝长度方向的夹角。

3）轴心力作用下圆形周边角焊缝的计算

对于圆形周边角焊缝每一处与轴力的夹角不同，βfθ实际是变化的，为方便实际工程中的钢管等圆形构件的角焊缝连接计算，可近似取βfθ=1.1。

4）轴心力作用下角钢与其他构件连接的角焊缝计算

角钢与其他构件用侧缝连接时（图3.36），由于角钢截面形心到肢背和肢尖的距离不相等，靠近形心的肢背焊缝承受较大的内力。设N1和N2分别为角钢肢背与肢尖焊缝承担的内力，由平衡条件可知：

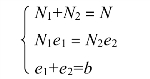
解上式得肢背和肢尖受力为：

式中　N——角钢承受的轴心力；

k1，k2——角钢角焊缝的内力分配系数，按表3.3采用。

图3.36　角钢的侧缝连接

表3.3　角钢角焊缝的轴力分配系数

在 N1和N2作用下，侧缝的直角角焊缝计算公式为：

式中　he1，he2——肢背、肢尖的有效焊缝厚度；

lw1，lw2——肢背、肢尖的焊缝计算长度。

考虑到每条焊缝两端的起灭弧缺陷，实际焊缝长度为计算长度加2hf；但对于三面围焊，由于在杆件端部转角处必须连续施焊，每条侧面角焊缝只有一端可能起灭弧，故焊缝实际长度为计算长度加 hf；对于采用绕角焊的侧面角焊缝，其实际长度等于计算长度（绕角焊缝长度2hf不进入计算）。

角钢用三面围焊时［图 3.37（a）］，既要考虑到焊缝形心线基本上与角钢形心线一致，又要考虑到侧缝与端缝计算的区别。计算时先选定端焊缝的焊脚尺寸 hf3，并算出它所能承受的内力：

式中　he3——端缝的有效焊缝厚度；

lw3——端缝的焊缝计算长度。

通过平衡关系得肢背和肢尖侧焊缝受力为：

在N1和N2作用下，侧焊缝的计算公式与式（3.24）相同。

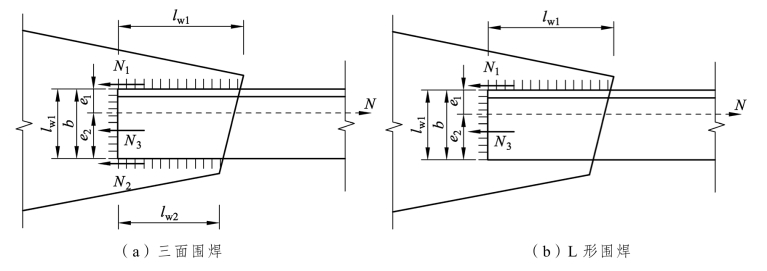
图3.37　角钢角焊缝围焊的计算

当采用L形围焊时［图 3.37（b）］，令N2＝0，由式（3.27）得：

L 形围焊角焊缝的计算公式为：

【例3.3】 试设计用两条侧焊缝和三面围焊进行连接的拼接盖板尺寸（图3.38）。已知钢板宽 B＝270 mm，厚度 t1＝28 mm，拼接盖板厚度 t2＝16 mm。该连接承受静态轴心力 N＝1 400 kN（设计值），钢材为 Q235B，手工焊，焊条为 E43 型。

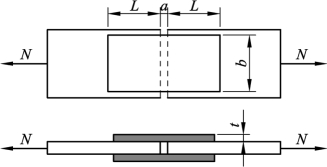
图3.38　例3.3拼接盖板

【解】 t1＝28 mm，=10 mm。

（1）采用两面侧焊

焊缝总长度

一条焊缝的实际长度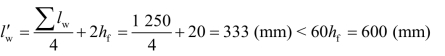

盖板长度

选定拼接盖板宽度 b＝240 mm，则：

满足强度要求。

根据构造要求可知，盖板应加横向角焊缝或中间塞焊。 故选定拼接盖板尺寸为 680 mm×240 mm×16 mm。

（2）三面围焊

选定拼接盖板宽度　b＝240 mm

端面角焊缝承担

侧面角焊缝承担(www.xing528.com)

侧面角焊缝长度

侧面一条角焊缝的实际长度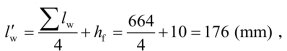取为180 mm

盖板长度

故选定拼接盖板尺寸为 370 mm×240 mm×16 mm。

【例3.4】 试确定图3.39所示承受静态轴心力作用的三面围焊连接的承载力及肢尖焊缝的长度。已知角钢为2 125∠×10，与厚度为 8 mm 的节点板连接，其肢背搭接长度为 300 mm，焊脚尺寸均为 hf＝8 mm，钢材为 Q235B，手工焊，焊条为E43 型。

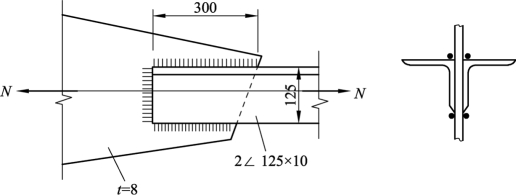
图3.39　例3.4三面围焊连接

【解】 正面角焊缝所能承受的内力 N3为（双角钢）：

肢背角焊缝所能承受的内力 N1为（双角钢）：

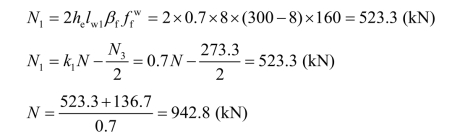
计算肢尖焊缝承受的内力 N2为：

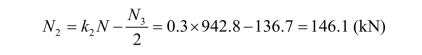
肢尖焊缝的长度为：取为 90 mm

3．在弯矩、轴力和剪力共同作用下的角焊缝计算

角焊缝在弯矩、剪力和轴力共同作用下的内力，根据焊缝所处位置和刚度等因素确定。角焊缝在各种外力共同作用下的内力计算原则是：

（1）首先求单独外力作用下角焊缝的应力，并判断该应力对焊缝产生端缝受力（垂直于焊缝长度方向），还是侧缝受力（平行于焊缝长度方向）。

（2）采用叠加原理，将各种外力作用下的焊缝应力进行叠加。叠加时注意应取焊缝截面上同一点的应力进行叠加，而不能用各种外力作用下产生的最大应力进行叠加。因此，应根据单独外力作用下产生的应力分布情况判断最危险点进行计算。

（3）如图3.40所示，在轴力N作用下，在焊缝有效截面上产生均匀应力，即：

式中　σN——由轴力N在端缝中产生的应力；e

Ae——焊缝有效截面面积。

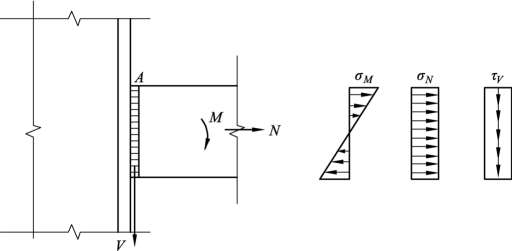
图3.40　弯矩、轴力和剪力共同作用的角焊缝应力

（4）在剪力 V 作用下，判断哪一部分焊缝截面承受剪力作用，在受剪截面上应力分布是均匀的，即：

式中τV——剪力 V 产生的应力。

（5）在弯矩M作用下，焊缝应力按三角形分布，即：

式中Mσ——弯矩在焊缝中产生的应力；

We——焊缝计算截面对形心的截面模量。

将弯矩和轴力产生的应力在A点叠加

剪力V在A点的应力τf=τV。

焊缝的强度验算公式为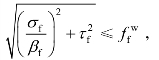当连接直接承受动力荷载时，取fβ=1.0。

如图 3.41 所示的工字形或H形截面梁与钢柱翼缘的角焊缝连接，通常承受弯矩M和剪力V的共同作用。计算时通常假设腹板焊缝承受全部剪力，弯矩则由全部焊缝承受。

为了焊缝的分布较合理，宜在每个翼缘的上下两侧角焊缝，由于翼缘焊缝只承受垂直于焊缝长度方向的弯曲应力，所以此弯曲应力沿梁高度呈三角形分布，最大应力发生在翼缘焊缝的最外纤维处。为了保证此焊缝的正常工作，应使翼缘焊缝最外纤维处的应力满足：

式中　M ——全部焊缝所承受的弯矩；

IW——全部焊缝有效截面对中心轴的惯性矩。

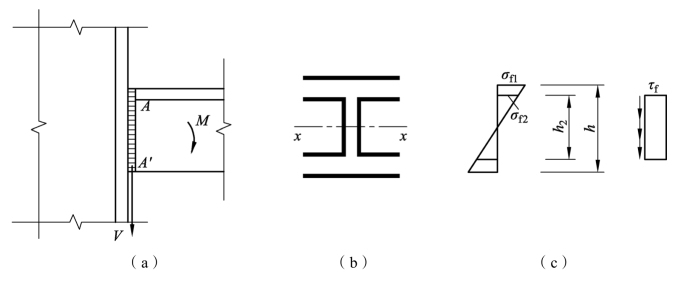
图3.41　工字形或H形截面梁的角焊缝连接

腹板焊缝承受两种应力共同作用，即垂直于焊缝长度方向且沿梁高呈三角形分布的弯曲应力和平行于焊缝长度方向且沿焊缝截面均匀分布的切应力的作用，设计控制点为翼缘焊缝与腹板焊缝的交点A。此处的弯曲应力和切应力分别按下式计算：

式中——腹板焊缝有效面积之和。

腹板焊缝在点 A 处的强度验算式为

工字形或H形截面梁与钢柱翼缘的角焊缝连接中，由于翼缘板的抗剪能力极差，有时也用另一种计算方法，假设腹板焊缝只承受剪力，翼缘板焊缝承担全部弯矩，此时弯矩M可以化为一对水平力 H＝M/h，则翼缘焊缝的强度计算公式为：

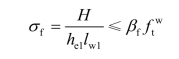
腹板焊缝的强度计算公式为：

式中——一个翼缘板上角焊缝有效面积之和；

——两条腹板焊缝有效面积。

【例3.5】 试验算如图3.42所示牛腿与钢柱连接角焊缝的强度。钢材为Q235，焊条为 E43 型，手工焊，荷载设计值 N＝365 kN，偏心距 e＝350 mm，焊脚尺寸hf1＝8 mm，hf2＝6 mm。图 3.42（b）为有效截面。

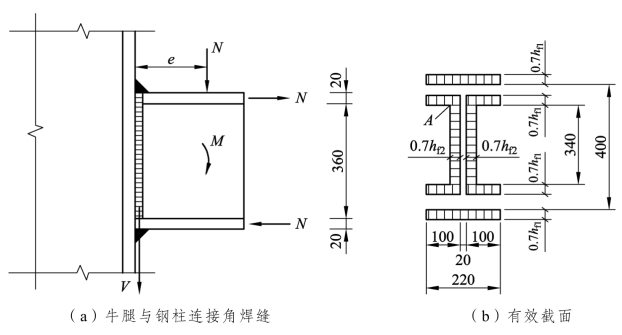
图3.42　例3.5图

【解】 N力在角焊缝形心处引起剪力V＝N＝365 kN

N 力在角焊缝形心处引起弯矩M＝Ne＝365×0.35 kN·m＝127.8 kN·m

（1）考虑腹板焊缝承受弯矩的计算方法

全部焊缝有效截面对中和轴的惯性矩为：

翼缘焊缝的最大应力：

腹板焊缝由弯矩 M 引起的最大应力：

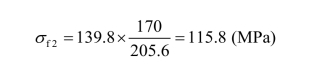
剪力 V 在腹板焊缝产生的平均剪应力：

则腹板焊缝的强度（A 点为设计控制点）为：

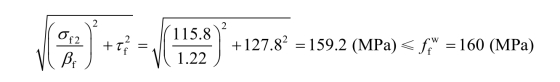
（2）不考虑腹板焊缝承受弯矩的计算方法

翼缘焊缝所承受的水平力：

翼缘焊缝的强度：

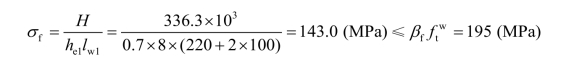
腹板焊缝的强度：

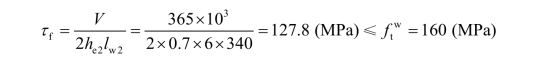
4．扭矩、剪力和轴力共同作用的角焊缝连接计算

图 3.43 所示为采用三面围焊的搭接连接，该连接角焊缝承受竖向剪力V F=和扭矩作用，对该连接角焊缝计算时假定：构件是完全刚性的，角焊缝处于弹性状态；角焊缝群上任意一点的应力方向垂直于该点与形心的连线，且应力大小与连线长度 r 成正比。

图3.43　剪力和扭矩作用下牛腿角焊缝应力

在剪力作用下，三面围焊焊缝视为均匀承受剪力，其值为：

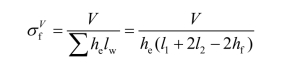
在扭矩作用下，焊缝最危险点为 A(A′) 点。A(A′) 点的应力为：

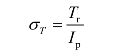
式中　Ip——焊缝截面的极惯性矩，Ip=Ix+Iy。

将Tσ沿x轴和y轴分解：

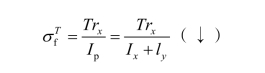
故A(A′)点的验算公式为：

上述应力计算时没有考虑焊缝方向（不区分正面角焊缝和侧面角焊缝），应力假定为平均分布，实际上在剪力作用下，对水平焊缝为正面角焊缝，竖直焊缝为侧面焊缝，水平焊缝承担的应力大于竖直焊缝，只在最后验算中引入系数fβ，上述计算方法有一定的近似性。

【例3.6】 如图 3.44 所示牛腿连接，采用三面围焊直角角焊缝。钢材用 Q235，焊条 E43 型，hf=10 mm 。在 a 点作用一水平力P1=50 kN ，竖向力P2=200 kN ，e1=200 mm ，e2=500 mm。验算该连接焊缝的强度。

图3.44　例3.6图

【解】 由于焊缝实际长度稍大于搭接长度，故可不扣除水平焊缝起落弧的缺陷。

焊缝形心至竖向焊缝的距离：

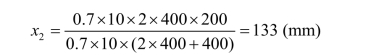
焊缝几何特性：

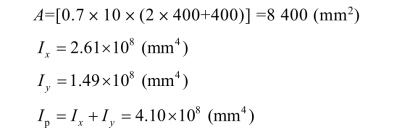
焊缝受力为：

焊缝最危险点为a点，则：

该连接的焊缝强度满足要求。