结构钢材在复杂应力下的屈服条件

钢材在单向拉伸作用状态下，当应力小于屈服点fy时，在弹性状态下工作；而当应力达到fy时，钢材则在塑性状态下工作。

在实际钢结构中，有些构件往往同时承受双向或二向复杂应力的作用，如实腹梁的腹板。这时候钢材的屈服并不只取决于某一方向的应力，而是由综合反映各个方向应力影响的强度理论来确定。对于接近理想弹性-塑性体的结构钢材，最适合的是用材料力学中的能量强度理论来确定钢材在多轴应力状态下的屈服条件。

根据材料力学可以导出，复杂应力作用下钢材由弹性状态转变为塑性状态的条件（见图 2.18），用折算应力epσ和钢材在单向应力时的屈服点fy的关系来判断。

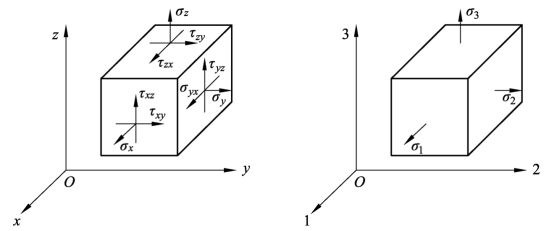
图2.18　钢材的复杂应力状态

当折算应力用主应力表示时：

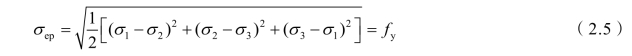
当折算应力用应力分量表示时：

这就是当钢材处于三向应力状态时，应以折算应力达屈服点为强度极限状态，作为进行强度设计时的标准。引入材料分项系数，得设计公式：

(www.xing528.com)

由公式（2.5）可见，当3个主应力均为压应力且又很接近时，即使σ1、σ2、σ3的数值很大，大大超过屈服点，但由于其差值不大，折算应力并不大，材料就不容易屈服而破坏。相反，当主应力中有异号应力，而同号的两个应力差又较大时，当最大的应力尚未达到fy时，折算应力就已达到fy而进入塑性状态了。

但要注意能量强度理论不适合三向受拉的应力状态。研究表明，即使是塑性材料在三向受拉时也容易发生脆断破坏，因此，在钢结构设计中，应尽量避免产生三向受拉状态。

因此，钢材在多轴应力状态下，当处于同号应力场时，钢材易产生脆性破坏；而当处于异号应力场时，钢材将发生塑性破坏。

平面应力时，折算应力可简化为：

一般的梁中，只存在正应力与剪应力，上式化为：

当钢材受纯剪时，σ=0，极限屈服状态为：

即剪应力达到屈服点的 0.58 倍时，钢材进入塑性状态。所以钢材的抗剪设计强度fv取为 0.58f，f为钢材抗拉强度设计值。