空间直线相对于画面的位置,不外乎两种情况,要么平行,要么相交,如图11.9 所示。

图11.9 各种位置的直线
规律1:画面平行线的透视与自身平行,其基透视平行于基线或视平线。
画面平行线因平行于画面而无迹点和灭点,如图11.10 所示(铅垂线前已述及)。
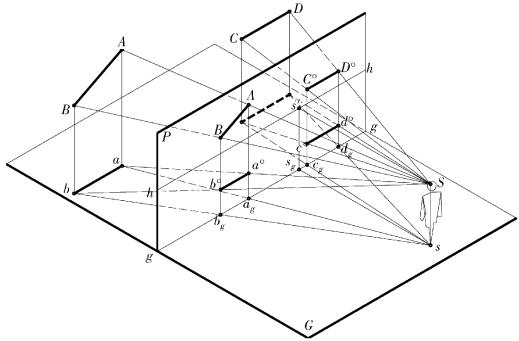
图11.10 画面平行直线的透视
规律2:与画面相交的直线在透视图上是有限的长度,一组平行线共灭点。
由于灭点的定义为直线上离画面无穷远点的透视,因此空间中无限长的直线,当其与画面相交时,透视图上将表现为有限的长度,以灭点为结束端。
同时从图11.8 中灭点的作图过程可以看出:对于一组平行直线,从视点S 只能作出它们的一条平行线,只会和画面获得一个共同的交点。因此,一组平行直线有一个共同的灭点,同理,其基透视也有一个共同的基灭点。所以,一组平行线的透视及其基透视,分别相交于它们的灭点和基灭点,图11.4 中所表现的透视现象即反映出这一规律。
根据直线与画面相交角度的不同,又可以将此规律细化出以下几种不同情况:
①画面垂直线的画面垂足为其迹点,视心s′为其灭点。如图11.11 所示。由图可见,画面垂直线的透视永远位于其迹点T 与灭点s′的连线Ts′上;其基透视始终在迹点的基点t 与灭点s′的连线ts′上。

图11.11 画面垂直线的透视
②画面水平相交线因平行于基面,故其透视与基透视具有共同的灭点(F,f 重合于视平线上)。在图11.12 中,该灭点在画面的有限轮廓范围之外。
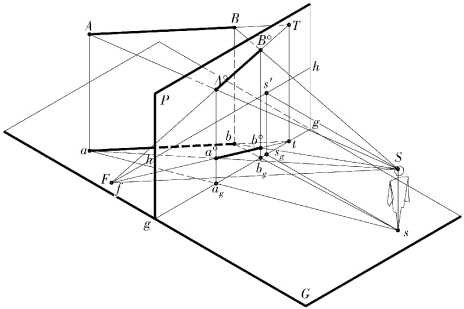
图11.12 画面水平相交线的透视
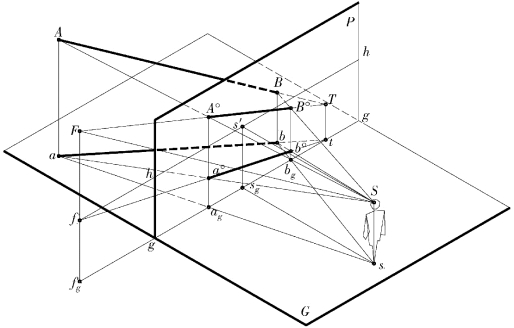
③一般位置的画面相交线:一般位置的画面相交线如图11.13 所示。图中,当A 点高于T点时称为“上行直线”;当A 点低于T 点时称为“下行直线”,它们的灭点位于过基灭点的同一铅垂线上。其中,上行直线的灭点在视平线上方,下行直线的灭点则在视平线的下方。在图11.13中,AB 直线的灭点与基灭点也超出了画面P 的图示有限范围。
规律3:垂直于基面的直线可以利用透视高度还原出真实高度。
当点位于画面上时,其透视为其自身,直线也相同。因此,当直线位于画面上时,其长度是真实的。这种能反映真实长度的直线中,有一种垂直相交于基线的画面铅垂线,因其反映直线的真实高度而被称为真高线。利用真高线,可以解决空间点的高度问题,也可以还原作出基面垂直线的真实高度。
 (https://www.xing528.com)
(https://www.xing528.com)
图11.13 画面一般相交线的透视
在图11.14(a)中,过A 点作任意方向的水平线AB 与画面相交于T,求出T 点的基点t,则Tt 就是一条能反映A 点真实高度Aa 的“真高线”。
为了求出A 点被透视以后在画面上呈现出的“透视高度”A°a°,可以先求出AT 及at 的透视TF 及tf。然后在求出A 点的基透视a°(在tf 上)后,过a°向上作铅垂线与TF 相交即可得到A点的透视高度A°a°。事实上,“透视高度”的确定意味着A 点的透视被求出,这也正是“真高线”的意义,作图过程如图11.14 所示(图中数字为作图步骤)。

图11.14 真高线及求法
按上述作图方法,还可以得出一个结论:求作某点的透视高度必须具备两个条件,一是该点的真高,二是该点的基透视。
作图时需注意:直线AT 是“任意”的,这种任意的结果是灭点F 的任意。所以在实际操作时,可在已知或已求出某点的基透视后,任定灭点并连接之。在图11.15 中,假设A 点的基透视a°已求出,A 点的真高等于H,则求A°的过程如下:
①在h-h 线上任定灭点F;
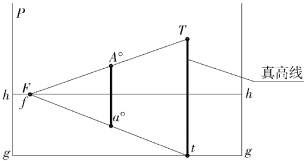
图11.15 灭点或真高线的任意性
②连接Fa°并延长之,使其与基线g-g 相交于t 点;
③过t 作铅垂线tT=H;
④连接tF;
⑤过a°向上作铅垂线交TF 于A°。
图中,在视平线上任意选定灭点F 后,连接a°F并延长,使其交基线g-g 于t,过t 即可作真高线。因为F 的任意性又导致了t 的任意性,于是,直接在基线上任选t 点,也可得出与上完全相同的结果。
在图11.16 中包含Aa 作矩形AaBb 平行于画面,并求出该矩形的透视A°B°a°b°,可以看到:A°B°与a°b°均平行于基线g-g,A°a°及B°b°均垂直于基线g-g。因此,平行于画面的矩形,其透视仍是矩形。即若AB 两点的空间高度相等,在与画面的距离也相等的前提下,其透视高度也是相等的。B 点的透视高度可以用为求A 点的透视高度而作的真高线来量取。通过这一原理,可以只用一条真高线,将空间任意多已知基透视和真高的点的透视高度或透视求出。这样的真高线,称为“集中真高线”。在图11.16(c)中,Tt 为集中真高线,B、C、D、E 四点虽然具有不同的空间位置与空间高度,但它们的“透视高度”或透视,均是通过Tt 而求出的。
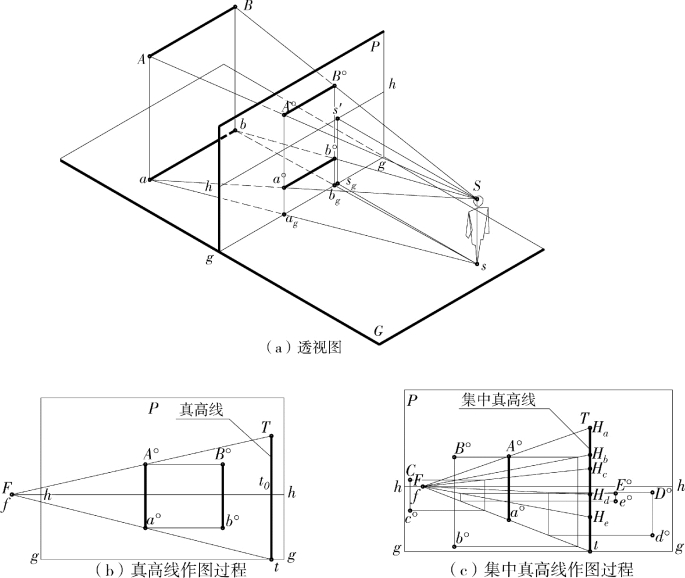
图11.16 集中真高线的原理及运用
同理,我们也可以逆向作图,利用辅助灭点,将已经作出的基面垂直线透视高度还原到画面位置上,获得真高线,从而确定该线的真实高度。
同时,垂直于基面的直线在与画面平行的前提下,自身比例不会产生透视变形。因此在图11.16 中,画面结果T 点到视平线的距离Tt0 与t 点到视平线的距离tt0 之比值,恰好等于真实的T 点和t 点与视平线高度的比值,其余各点相同。利用这一特性,在已知直线段真实高度和视平线高度的情况下,也可以利用上下高度的比值进行更为简便的高度作图;反之,也可以利用视平线高度作出简便的高度判断,此方法称为视平线定比例分割法。
通过点和直线的透视作图原理,任意“形”或“体”的透视均可求出,因为线由点构成,面由线构成。总之,从几何意义的角度看,通过“点”这一基本构成要素,再结合直线的透视规律,可以增进对各种透视现象与规律的把握,熟悉和深入理解各种作图方法与技巧。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




