土木工程制图：平面与圆锥的相交关系

当平面截割圆锥时，由于截平面与圆锥的相对位置不同，其截交线有以下5 种形状：

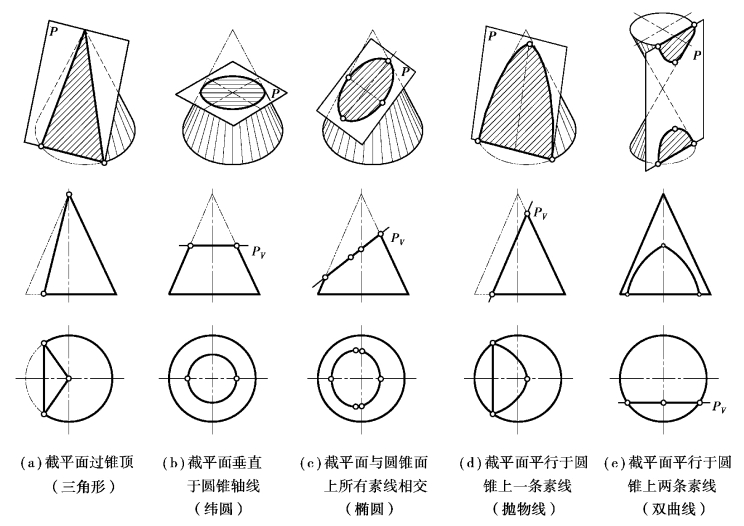
图7.36　平面截割圆锥

①当截平面过锥顶时，截平面与圆锥面的截交线为两条直素线，而截平面与圆锥体的截交线是一个过锥顶的三角形，如图7.36（a）所示。

②当截平面垂直于圆锥的回转轴时，其截交线是一个纬圆，如图7.36（b）所示。

③当截平面倾斜于圆锥的回转轴线，并与圆锥面上所有素线均相交时，其截交线为椭圆，如图7.36（c）所示。

④当截平面倾斜于圆锥的回转轴线，并平行于圆锥面上的一条素线时，其截交线为抛物线，如图7.36（d）所示。

⑤当截平面平行于圆锥面上的两条素线时，其截交线为双曲线，如图7.36（e）所示。

平面与圆锥相交所得的截交线圆、椭圆、抛物线和双曲线，统称为圆锥曲线。当截平面与投影面倾斜时，椭圆、抛物线、双曲线的投影，一般仍分别为椭圆、抛物线和双曲线，但有变形。

作圆锥曲线的投影，实际上是定属于锥面的点的问题。不论它是什么圆锥曲线，作图方法都相同。可用素线法或纬圆法或二者并用，求出截交线上若干点的投影，然后依次连接起来即可。(www.xing528.com)

【例7.8】作正垂面P 与圆锥的截交线的投影和截断面实形，如图7.37 所示。

图7.37　正垂面P 与圆锥的截交线和截断面实形

【解】分析：因截平面P 与圆锥轴线倾斜，并与所有素线相交，故截交线是一个椭圆。它的长轴平行于正立投影面，短轴垂直于正立投影面，并垂直平分长轴。椭圆的正面投影积聚在PV上。又因截平面P 倾斜于水平投影面，椭圆的水平投影仍为椭圆，但不反映实形，椭圆长、短轴的水平投影仍为椭圆投影的长、短轴。本例以纬圆法作图。

作图：如图7.37 所示。

①求特殊点：在正面投影中，PV 与圆锥正面投影轮廓素线的交点即为椭圆长轴ⅠⅤ两端点的正投影1′和5′，由此向下引投影连线得Ⅰ、Ⅴ的水平投影1、5；线段1′5′的中点3′（7′）是椭圆短轴Ⅲ、Ⅶ的两端点的正面投影，过Ⅲ、Ⅶ作纬圆，即可求出ⅢⅦ的水平投影3 和7；PV 与圆锥最前、最后素线的正面投影的交点4′（6′）是圆锥面的最前、最后素线与P 面的交点Ⅳ（Ⅵ）的正面投影，用纬圆法作出其水平投影4、6。

②用纬圆法求一般点Ⅱ、Ⅷ的水平投影2、8，在Ⅱ、Ⅷ（QV）位置作纬圆，在此纬圆的水平投影上，从2′8′向下作投影连线，即得Ⅱ、Ⅷ点的水平投影2 和8。

③在水平投影中，用光滑的曲线依次连接1—2—3—4—5—6—7—8—1 各点，便得椭圆的水平投影。

④用换面法作出长、短轴端点Ⅰ、Ⅴ、Ⅲ、Ⅶ和中间点Ⅳ、Ⅵ、Ⅱ、Ⅷ等点的新投影，新投影31、71 点间的距离等于水平投影3、7 间的距离。其他各点原理相同，画出的椭圆即截断面的实形。