土木工程制图中的圆柱体：定义、形成与投影

1）形成

由矩形（AA1O1O）绕其边（OO1）为轴旋转运动的轨迹称为圆柱体，如图7.25（a）所示。与轴垂直的两边（OA 和O1A1）的运动轨迹是上、下底圆，与轴平行的一边（A A1）运动的轨迹是圆柱面。A A1 称为母线，母线在圆柱面上的任一位置称为素线。圆柱面是无数多条素线的集合。圆柱体由上、下底圆和圆柱面围成，上、下底圆之间的距离称为圆柱体的高。

2）投影

（1）安放位置

为简便作图，一般将圆柱体的轴线垂直于某一投影面。如图7.25（b）所示，令圆柱体的轴线（OO1）垂直于H 面，则圆柱面垂直于H 面，上、下底圆平行于H 面。

（2）投影分析

投影分析如图7.25（b）所示。

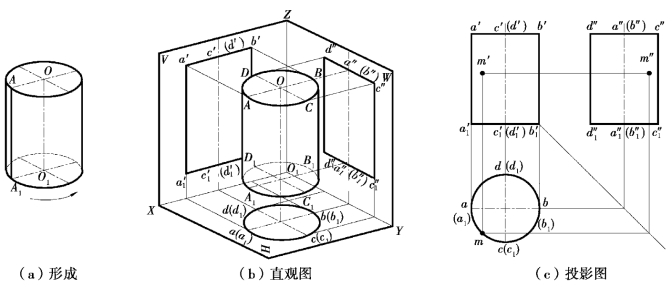
图7.25　圆柱体的形成与投影

H 面投影：为一个圆。它是可见的上底圆和不可见的下底圆实形投影的重合，其圆周是圆柱面的积聚性投影，圆周上任一点都是一条素线的积聚性投影。

V 面投影：为一矩形。它是可见的前半圆柱和不可见的后半圆柱投影的重合，其对应的H面投影是前、后半圆，对应的W 面投影是右和左半个矩形。矩形的上、下边线（a′b′和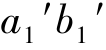）是上、下底圆的积聚性投影；左、右边线（a′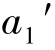和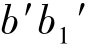）是圆柱最左、最右素线（AA1 和BB1）的投影，也是前半、后半圆柱投影的分界线。

W 面投影：为一矩形。它是可见的左半圆柱和不可见的右半圆柱投影的重合，其对应的H面投影是左、右半圆；对应的V 面投影是左和右半个矩形。矩形的上、下边线（d″c″和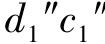是上、下底圆的积聚性投影；左、右边线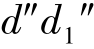（和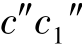）是圆柱最后、最前素线（DD1 和CC1）的投影，也是左半、右半圆柱投影的分界线。

（3）作图步骤[图7.25（c）](www.xing528.com)

①画轴线的三面投影（o、o′、o″），过O 作中心线，轴和中心线都画单点长画线。

②在H 面上画上、下底圆的实形投影（以O 为圆心，OA 为半径）；在V、W 面上画上、下底圆的积聚性投影（其间距为圆柱的高）。

③画出转向轮廓线，即画出最左、最右素线的V 面投影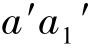（和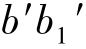）；画出最前、最后素线的W 面投影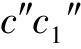（和）。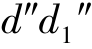

3）圆柱体表面上取点

【例7.3】已知圆柱体上M 点的V 面投影m′及N 点的H 面投影n，求M、N 点的另二投影，如图7.26（a）所示。

【解】分析：由于m′可见，且在轴o′左侧，可知M 点在圆柱面的前、左部分；n 不可见，则N 点在圆柱的下底圆上。圆柱面的H 面投影和下底圆的V 面、W 面投影有积聚性，可从积聚性投影入手求解。

作图：如图7.26（b）所示。

①由m′向下作垂线，交H 面投影中的前半圆周于m，由m′、m 及Y1 可求得m″。

②由n 向上引垂线，交下底圆的V 面积聚性投影于n′，由n、n′及Y2 可求得n″。

③判别可见性：M 点位于左半圆柱，故m″可见；m、n′、n″在圆柱的积聚性投影上，不判别其可见性。

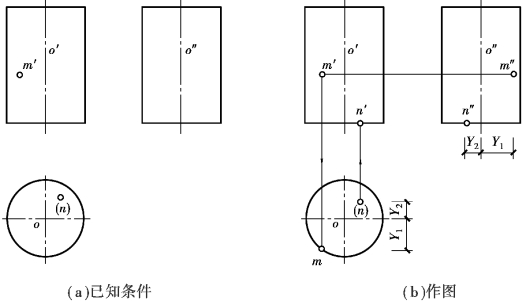
图7.26　圆柱体表面上取点