土木工程制图：两平面立体相交的作图方法

从图6.16 可看出：两平面立体相交产生的空间折线或平面多边形的各线段，是两平面立体相关表面产生的交线，折线的顶点是两平面立体相关棱线与表面的交点。所以，求两平面立体相交的相贯线问题，实质上是求直线（棱线）与平面（立体表面）的交点及求两平面（立体表面）交线的问题。

相贯线连线原则：属于某立体同一表面，同时也属于另一立体同一表面上的两点才能相连。

相贯线可见性判别原则：相贯线上的线段只有同时属于两立体可见表面上时，才为可见，否则为不可见。

当求出属于相贯线上的点之后，按照上述原则连接得到相贯线。应当注意：两立体贯穿后是一个整体，相贯线既是两立体表面共有线，也是两立体表面的分界线，立体表面的棱线只能画到相贯线处为止，不能穿入另一立体中，如图6.16 所示。

图6.16　两平面立体相交

【例6.10】如图6.17（a）所示，求两三棱柱的相贯线。

【解】分析：从图6.17（a）可看出，两三棱柱为互贯，三棱柱ABC 的棱线垂直于H 面，它的水平投影abc 具有积聚性，故属于其上的相贯线的水平投影为已知。又因三棱柱DEF 的棱线垂直于W 面，它的W 面投影d″e″f″具有积聚性，故属于其上的相贯线的W 面投影也为已知，只需求出相贯线的V 面投影，即可完成两三棱柱相交的投影。

作图：如图6.17（b）所示。

①三棱柱ABC 的H 面投影具有积聚性，可以确定它与三棱柱DEF 的交点1、2、（3）、（4）、5、（6）；三棱柱DEF 的W 面投影具有积聚性，也可以确定它与三棱柱ABC 的交点1″、（2″）、3″、（4″）、5″、6″。

②相贯线各点的V 面投影和W 面投影Ⅰ（1、1″）、Ⅱ（2、2″）、Ⅲ（3、3″）、Ⅳ（4、4″）、Ⅴ（5、5″）、Ⅵ（6、6″）均已知，即可求出它们的V 面投影1′、2′、3′、4′、5′、6′。

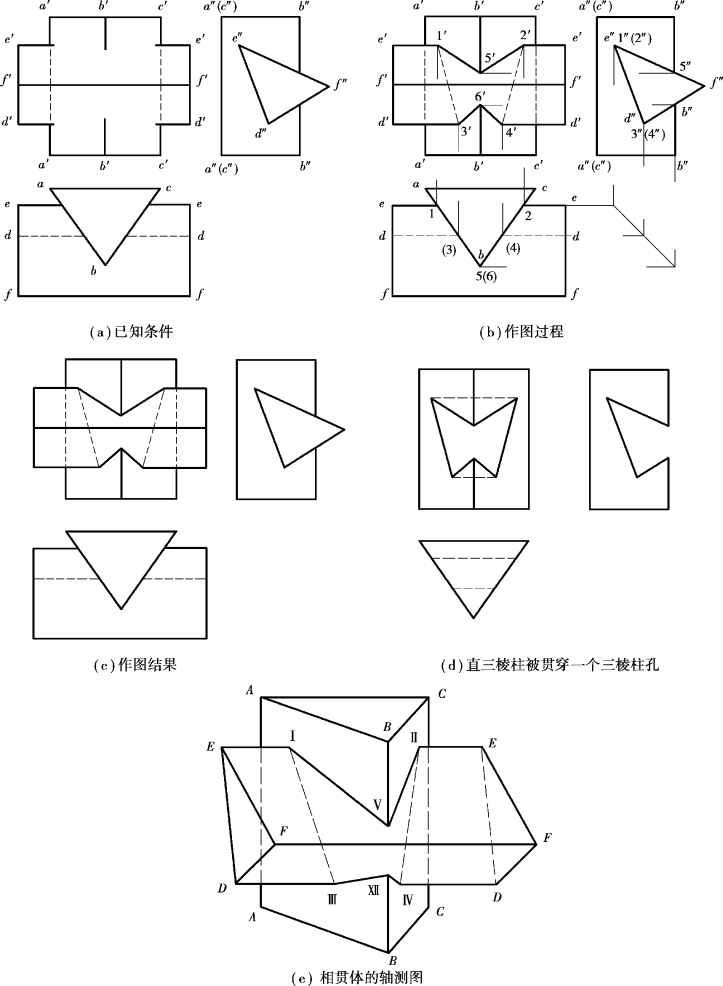
图6.17　两三棱柱相交

③根据相贯线的连线原则，从任一点开始连线，可按Ⅰ→Ⅴ→Ⅱ→Ⅳ→Ⅵ→Ⅲ→Ⅰ的顺序连线。在图6.17（b）的正投影中，将它们的同名投影相连，即得相贯线的正投影，为封闭的空间折线。

④判定可见性。根据相贯线上的线段，只有同时属于两立体可见表面时才可见的原则，在图6.17（b）的正面投影中，判断1′5′、2′5′、3′6′、4′6′线段为可见；1′3′、2′4′线段为不可见，完成相贯线的可见性判定。同时，判断出三棱柱ABC 的AA 棱线、BB 棱线被遮住部分不可见，完成两三棱锥相交后的投影。

若相交的两立体一个为实体、一个为虚体，相贯线的求解方法与两实体相交时完全相同。如图6.17（d）所示，可看成是将三棱柱DEF 沿水平方向抽出（形成虚体）。同时，应注意相贯线可见性与图6.17（c）的变化，以及新出现的虚线。

【例6.11】如图6.18（a）所示，求三棱锥与四棱柱相交后的投影。

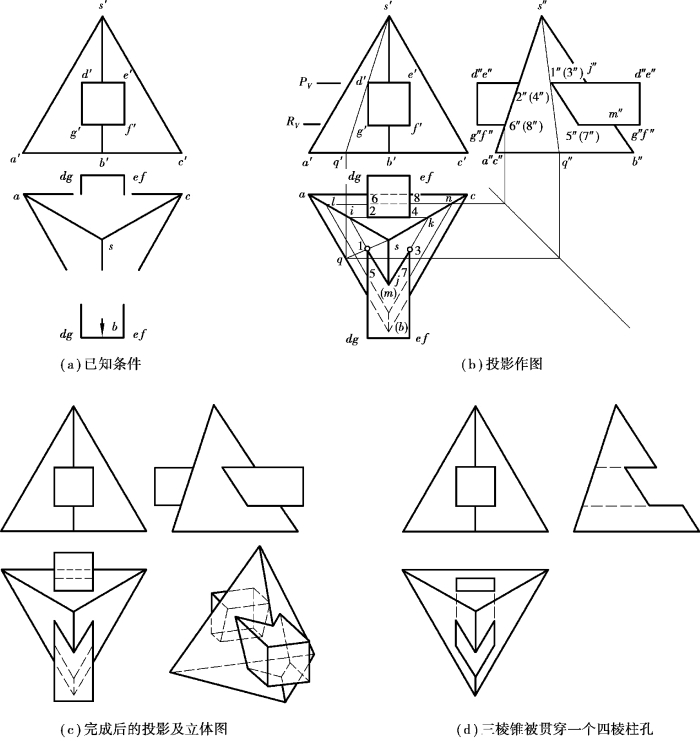
图6.18　三棱锥与四棱柱相贯

【解】分析：①四棱柱的四条棱线均正垂线，故其V 面投影具有积聚性，属于四棱柱表面的相贯线的V 面投影为已知。

②从正投影观察，四棱柱完全贯穿三棱锥，为全贯，从水平投影观察，四棱柱“穿入”“穿出”三棱锥，所以相贯线有前后两组。

③三棱锥的底面是水平面，四棱柱上下表面为水平面，左右表面为侧平面。它们相交后产生的相贯线，将分别属于四棱柱的水平及侧平表面上。

④投影图左右对称，所以相贯线也是左右对称的。

作图：如图6.18（b）所示，分别采用辅助线法和辅助面法。

①辅助线法：要求四棱柱DD 棱线与三棱锥表面的交点，可利用DD 棱线正投影的积聚性，连s′d′到q′，s′q′为三棱锥SAB 表面上过I 点的一辅助线，按投影关系求出sq、s″q″，其上的1、1″即为贯穿点Ⅰ的两个投影。同理，可求出贯穿点Ⅱ、Ⅲ、Ⅳ、Ⅴ、Ⅵ、Ⅶ、Ⅷ的投影，又有棱线SB 与四棱柱上下表面的交点J、K，便求出了相贯线上各点的投影。(www.xing528.com)

②辅助面法：要求三棱锥表面与四棱柱表面的交线，可作包含四棱柱上表面DDEE 平面的水平面PV 及包含四棱柱下表面GGFF 平面的水平面RV，与三棱锥相交产生截交线△IJK 和△LMN。这两组交线分别与四棱柱4 条棱线相交于Ⅰ、Ⅱ、Ⅲ、Ⅳ、Ⅴ、Ⅵ、Ⅶ、Ⅷ点，同时与三棱锥SB 棱线交于J、M 点，便求出了相贯线上各线段的投影。

③根据相贯线的连线原则，可得三棱锥与四棱柱全贯后前、后两部分的相贯线，前面为封闭的空间折线，后面为封闭的平面多边形。它们的W 面投影具有积聚性和重影性。

④判定可见性。根据同时属于两立体可见表面的相贯线线段才可见的原则，判断属四棱柱上表面的相贯线段为可见，属于四棱柱下表面的相贯线为不可见。同时，判断两立体相交后，三棱锥底面被四棱柱遮住部分的投影不可见，如图6.18（c）所示。

如图6.18（d）所示为一个实体的三棱锥被一虚体的四棱柱相贯穿后（将四棱柱沿水平方向抽出）的投影图，其作图方法与上述相同，应注意对比两种情况下相贯线可见性、三棱锥可见性的变化及新出现的虚线。

【例6.12】如图6.19（a）所示，求正六棱柱被一个三棱柱穿孔后的投影。

【解】分析：从正六棱柱被穿孔的V 面投影和正六棱柱具有积聚性的H 面投影可以看出，正六棱柱被穿孔后，前后、左右均是对称的。前面孔口是正三棱柱的三个棱面与正六棱柱的左前、前、右前三个侧表面产生的交线，分别为ⅠⅡ、ⅡⅢ、ⅢⅣ、ⅣⅤ、ⅤⅥ、ⅥⅦ、ⅦⅠ。交线的V 面投影为已知，交线的H 面投影积聚在正六棱柱的H 面投影中（在前面）；后面孔口为正三棱柱的三个棱面与正六棱柱的左后、后、右后3 个侧表面产生的交线，分别为Ⅰ0 Ⅱ0、Ⅱ0 Ⅲ0、 Ⅲ0 Ⅳ0、Ⅳ0Ⅴ0、 Ⅴ0Ⅵ0、 Ⅵ0Ⅶ0、 Ⅶ0Ⅰ0。前后两组交线具有对称性，如它们的正投影重影，水平投影积聚在正六棱柱的H 面投影中（在后面）。

作图：如图6.19（c）所示。

①确定出前面孔口所产生的相贯线上各点Ⅰ、Ⅱ、Ⅲ、Ⅳ、Ⅴ、Ⅵ、Ⅶ的V 面投影1′、2′、3′、4′、5′、6′、7′；后面孔口所产生的相贯线上各点与之对称，有。

②这14 个点分别属于正六棱柱前后6 个侧表面，正六棱柱各表面的H 面投影具有积聚性，从而确定出这14 个点的H 面投影。

③相贯线上各点的H 面投影和V 面投影均已知，便可求出相贯线上各点的W 面投影。

④根据相贯线的连线原则，并对照V 面投影和H 面投影，进行相贯线W 面投影的连线：1″→2″→3″→4″→5″→6″→7″→1″及。

⑤判断可见性。正六棱柱被正三棱柱穿孔，所以穿入正六棱柱内部的棱线均不可见，应画成虚线。

图6.19　求正六棱柱被正三棱柱穿孔后的相贯线

【例6.13】如图6.20（a）所示，求三棱锥与正四棱锥相交后的投影。

【解】分析：①三棱锥的V 面投影具有积聚性，所以，属于三棱锥表面的相贯线的V 面投影已知。

②通过对题目的观察可知，三棱锥完全贯穿正四棱锥，且“穿入”“穿出”正四棱锥，所以相贯线应有各自独立的前后两组。

③两相贯体前后具有完全的对称性，所以，前后两组各自独立的相贯线也是对称的。

作图：采用辅助平面法求解，如图6.20（b）所示。

①在V 面投影中，包含三棱柱底面（水平面）作辅助平面PV，它与正四棱锥产生一平行于四棱锥底边截交线，其中有效交线为前面部分Ⅰ→Ⅱ→Ⅲ、后面部分Ⅰ0→Ⅱ0→Ⅲ0。由V 面投影1′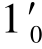（）→2′（）→3′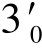（）求出H 面投影1（10）→2（20）→3（30）和W 面投影1″（）→2″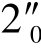（）→3″（3″0）。

②在V 面投影中，包含三棱柱最上面的棱线作一辅助平面QV，同样产生一平行于四棱锥底边截交线，其中有效交点为Ⅴ、Ⅴ0，即由5′（）求出5（50）和5″（）。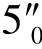

③在V 面投影中，正四棱锥的最前、最后棱线分别与三棱锥的右侧面和底面相交，故分别产生交点Ⅳ、Ⅳ0 及Ⅱ、Ⅱ0，其中Ⅱ、Ⅱ0 前面已经求出，Ⅳ、Ⅳ0 的求解根据直线上点的从属性，便可由4′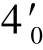（）求出4″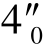（）和4（40）。

④根据相贯线的连线原则，可得前后两组相贯线分别按Ⅰ、Ⅰ0 →Ⅱ、Ⅱ0 →Ⅲ、Ⅲ0 →Ⅳ、Ⅳ0→Ⅴ、Ⅴ0→Ⅰ、Ⅰ0 的顺序连接，它们的V 面投影前后重影、H 面投影和W 面投影后对称。

⑤判断可见性。根据同时属于两立体可见表面的线段才可见的原则，判断H 面投影中属于三棱柱底面的前、后各两段线段为不可见，W 面投影中属于正四棱锥右侧面的前、后各三段线段为不可见。

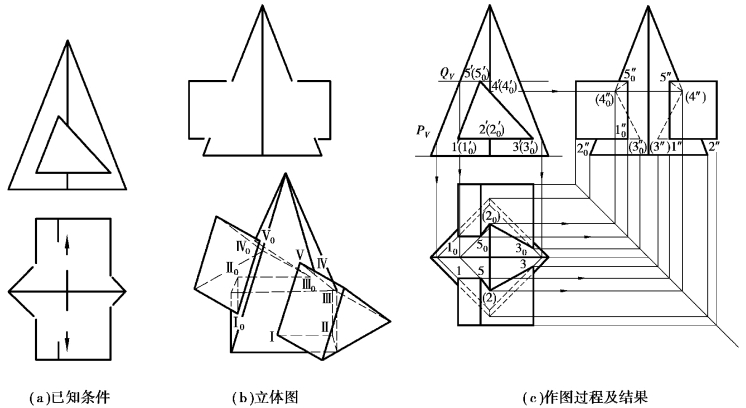
图6.20　求三棱柱与正四棱锥的相贯线