直线或平面立体投影具有积聚性|土木工程制图

【例6.7】如图6.13（a）所示，求直线MN 与三棱柱的贯穿点。

【解】分析：从图6.13（a）所示的水平投影中可知，三棱柱的水平投影具有积聚性，直线MN贯穿过三棱柱的左右侧棱面。所以，贯穿点的水平投影可直接得到。再由直线上点的从属性，可求出贯穿点的正投影。

作图：如图6.13（b）所示。

①求贯穿点的水平投影。线段mn 与三棱柱左右侧面的积聚性水平投影的交点，即为贯穿点的水平投影1，2。

②求贯穿点的正面投影。根据直线上点的从属性，由水平投影1、2 求出正面投影1′、2′。

③判断可见性。根据Ⅰ、Ⅱ点所属三棱柱左、右侧棱面的可见性，判断1′、2′均可见。

必须注意：直线穿入立体时，与立体已融为一整体，故直线在立体内部的一段并不存在，不能画线。

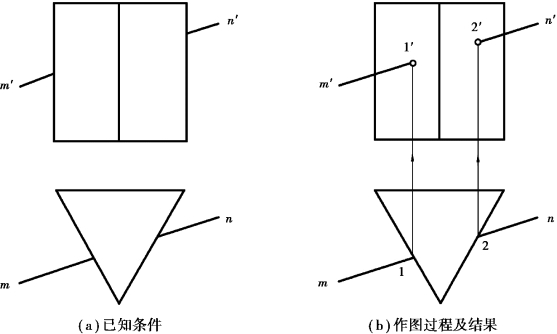
图6.13　求一般位置直线与三棱柱的贯穿点(www.xing528.com)

【例6.8】如图6.14（a）所示，求正垂线ED 与三棱锥的贯穿点。

【解】分析：正垂线ED 的正投影具有积聚性，故属于DE 直线的贯穿点其正投影必定与积聚点重合，即贯穿点的正投影为已知。用立体表面取点法即可求出贯穿点的其余两个投影。

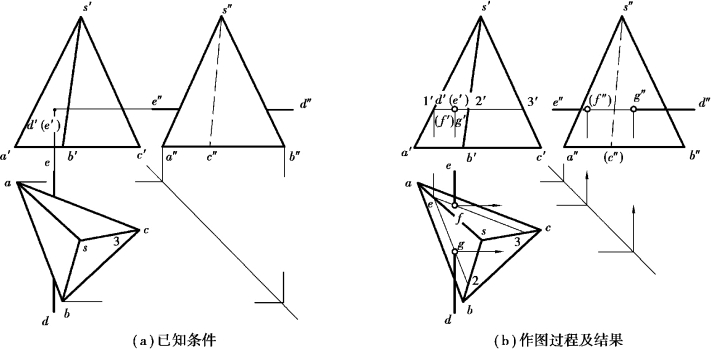
图6.14　求正垂线与三棱锥的贯穿点

作图：如图6.14（b）所示。

①求贯穿点的水平投影。由DE 的正投影积聚，直接得到贯穿点F、G 的正投影f′、g′。

②求贯穿点的水平投影。由立体表面取点的方法，过f′作1′2′∥a′b′，过m′作1′3′∥a′c′，求得贯穿点的水平投影f ，g 和侧投影f″、g″。

③判断可见性。由贯穿点所属表面的可见性，分别判断出G 点的三面投影均可见；F 点的H 投影可见，V、W 投影不可见，由此完成直线贯穿立体后的投影。同样要注意的是，直线穿入立体内部后，两贯穿点之间不能画线。