底面为平面多边形,其余各侧面都是三角形,且各侧棱相交于一个顶点的平面立体称为棱锥。棱锥底面的边数与侧面数、侧棱数相等,当底面边数为N 时(底面是N 边形),就称为N 棱锥(N≥3)。
顶点到底面的距离称为棱锥的高。当棱锥的底面为正多边形,且棱锥的顶点与该正多边形中心的连线即为棱锥的高,与底面垂直,则该棱锥被称为正棱锥;反之,则为斜棱锥。
下面以正三棱锥为例对棱锥的特征、安放、投影作图等进行讲解。
(1)棱锥的特征
如图6.3(a)所示,棱锥有以下3 个特征:
①底面为多边形,如图6.3(a)中底面为△ABC。
②每个侧面均为三角形,如图6.3(a)中侧面分别为△SAB、△SBC、△SAC。
③每条侧棱均交于同一顶点,如图6.3(a)中SA、SB、SC 均交于顶点S。
(2)棱锥的安放位置
安放原则:使棱锥的底面平行于某一投影面,顶点通常朝上、朝前或朝左。
如图6.3(a)所示,使三棱锥的底面△ABC 平行于H 面,后侧面△SAC 垂直于W 面。
(3)棱锥的投影作图(https://www.xing528.com)
作棱锥的投影,就是画出该棱锥底面及各侧面的投影。
作图:如图6.3(b)所示。
①画底面△ABC 的实形投影(△abc)和积聚性投影[a′b′c′、a″(c″)b″];
②画顶点S 的三面投影(s、s′、s″);
③连各侧棱的三面投影,完成棱锥的投影作图。
(4)棱锥的投影分析
棱锥的H、V、W 面各个投影,应包含该棱锥所有表面的该面投影,如图6.3(b)所示。
水平面投影:由若干个小三角形组合而成,小三角形的数量由底面边数决定,是该棱锥各个侧面的类似形投影与底面的实形投影的重合(各侧面可见,底面不可见),图6.3(b)所示为由三个小三角形组合成的大三角形。
正面投影:基本形状为三角形,图6.3(b)所示为左右两个小三角形合成的一个大三角形。左右两个小三角形是棱锥左右侧面类似形投影(可见),大三角形是后侧面的类似形投影(不可见),大三角形的下边线是棱锥底面的积聚性投影。
侧面投影:基本形状为三角形,图6.3(b)中三角形是三棱锥左右侧面的类似形投影的重合(左侧面可见,右侧面不可见),三角形的左边线及底边线是棱锥后侧面及底面的W 面积聚投影,三角形右边线是前侧棱(SB)的W 面投影。
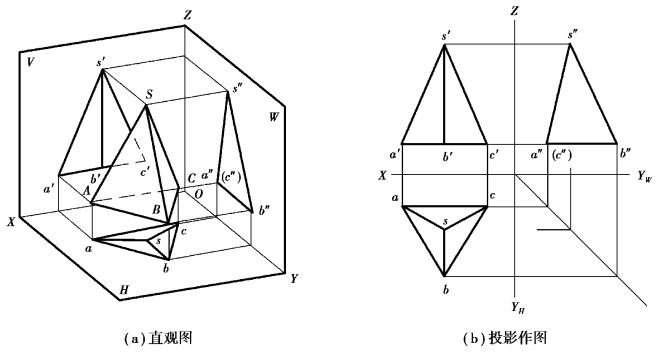
图6.3 三棱锥的投影
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




