1)实长和实形
(1)直线段的实长
特殊位置直线在所平行的投影面上的投影反映其实长。一般位置直线段可用直角三角形法求其实长。
(2)平面图形的实形
平行面在所平行的投影面上的投影反映平面图形实形。其他位置平面图形可依据最基本的平面多边形──三角形,用直角三角形法求出三角形三条边的实长,再按已知三边作出三角形的实形。所有的平面多边形均可分为若干个三角形,求得各三角形实形后,就能拼画成多边形的实形。
2)有关距离的量度
(1)两点之间的距离
两点连成直线,该直线的实长即为两点之间的距离。
(2)点到直线的距离、两平行线间的距离
若直线为垂直线,其积聚性投影与已知点同面投影的距离即为点到直线的距离,如图4.30(a)所示;若直线为平行线,在平行的投影面上可直接作出已知点到已知平行线的垂线,并得到垂足,求垂足与已知点的连线长度即得所求点到直线得距离,如图4.30(b)所示。

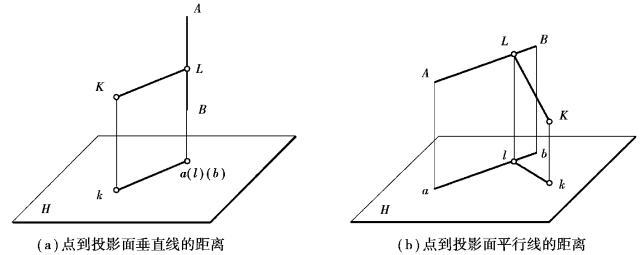
图4.30 点到特殊位置直线的距离
如图4.31(a)所示,求点到一般位置直线的距离,其作图步骤为:
①过点K 作平面P 垂直于已知直线MN。
②求出平面P 与MN 的交点,即垂足G。
③连接已知点K 和垂足G,求KG 的实长。该实长即为点到直线的距离。
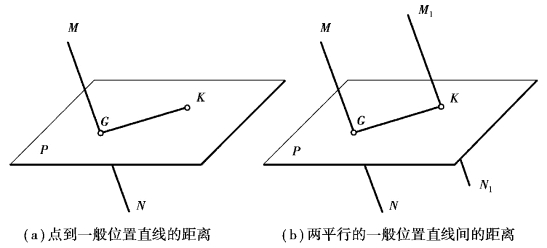
图4.31 点到直线的距离、两平行线间的距离
两平行线间的距离,可视为直线M1 N1 上的任一点K 到直线MN 的距离,其空间作图步骤与点到一般位置直线的距离作图步骤类似,如图4.31(b)所示。
(3)点到平面、相互平行的直线和平面之间的距离、两平行平面间的距离
若平面为特殊位置平面,点到平面的距离就是平面积聚性投影与点的同面投影的距离,如图4.32 所示。


图4.32 点到特殊位置平面的距离
如图4.33(a)所示,求点到一般位置平面的距离,其作图步骤为:
①过已知点K 向平面P 作垂线。
②求出此垂线与平面P 的交点,即垂足G。
③求KG 的实长,即得点与一般位置平面的距离。

图4.33 点到平面、直线与其平行平面、平行平面的距离
如图4.33(b)所示,相互平行的直线和平面的距离,可视为直线MN 上任一点K 到平面P的距离;如图4.33(c)所示,平行平面P、Q 间的距离,可视为平面P 上任一点K 到平面Q 的距离。作图方法都可以利用求点到平面的距离的方法作图。(https://www.xing528.com)
3)交叉两直线的最短距离
交叉两直线的最短距离即交叉两直线的公垂线的长度。若交叉两直线有一条直线为投影面垂直线,则其最短距离为从垂直线积聚为点的投影,到另一直线的同面投影的垂线段的长度,如图4.34(a)所示;当然若交叉两直线均为某投影面的平行线,则其最短距离为两平行线的类似投影的间距,如图4.34(b)所示。
如图4.34(c)所示,求交叉两直线M 和M1 间最短距离的空间作图步骤为:
①包含直线M1 作平面P,P 平行于直线M。
②求相互平行的直线M 和平面P 之间的距离,此距离即为交叉两直线M 和M1 之间的最短距离。
如果还要求出公垂线,则空间作图步骤为[如图4.34(d)所示]:
①包含直线M1 作平面P 平行于直线M。
②自属于直线M 的任一点A 作平面P 的垂线,并求出垂足B。
③过垂足B 作直线M2 平行于已知直线M,且与已知直线M1 交于点G。
④过点G 作直线平行于上述垂线AB,与已知直线M 交于点K。KG 即为直线M 和M1 的公垂线,其实长为直线M、M1 的最短距离。
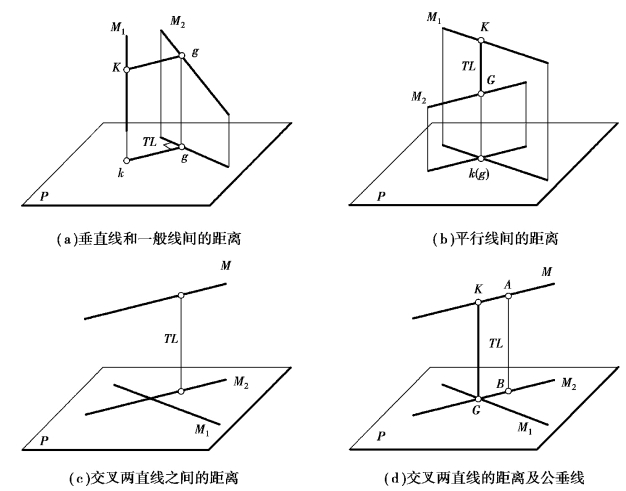
图4.34 交叉两直线的最短距离(TL)及公垂线KL
4)有关角度的量度
(1)相交二直线的夹角
如图4.35 所示,以相交直线AB、AC 为两边,可连成△ABC,求出△ABC 的实形即得相交直线AB、AC 的夹角α。
(2)直线与平面的夹角
如图4.36 所示,求直线AB 与平面P 的夹角的空间作图步骤为:
①过直线上任一点B 向平面P 作垂线;
②求出相交直线BC、BD 的夹角δ(取第三边为投影面平行线较简便,如图4.36 中第三边CD∥PH∥H);
③δ 的余角(90° -δ),即为直线与平面的夹角θ。
(3)两平面的夹角
如图4.37 所示,求两平面P、Q 夹角的空间作图步骤为:
①过空间任一点K 分别向P、Q 两平面作垂线KA、KB。相交二直线KA、KB 所构成的平面是P、Q 二平面的公垂面。
②求出相交二直线KA、KB 的夹角ω(取第三边为投影面平行线,参考图4.36)。
③ω 的补角(180° -ω)即为P、Q 两平面的夹角φ。
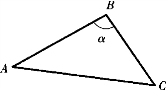
图4.35 相交两直线的夹角

图4.36 直线与平面的夹角
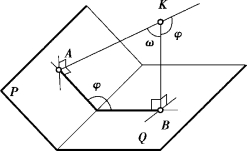
图4.37 两平面的夹角
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




