如何判断直线和平面是否垂直

1）几何条件及其投影特点

直线垂直平面的几何条件是：若直线垂直于平面内的任意两条相交直线，则该直线必与平面垂直。

为直接在投影图中反映垂直关系，应该选择属于平面的投影面平行线，此时就可以直接运用直角投影定律反映垂直关系。根据初等几何原理，若直线垂直于平面，则该直线必垂直于平面内的所有直线，自然也包括平面内的平行于投影面的直线，如图4.22（a）所示。

由此可以推出直线垂直平面的投影特点是：

①若直线垂直于平面，则该直线的H 投影一定垂直于平面内的水平线的H 投影（包括平面的水平迹线），直线的V 投影一定垂直于平面内的正平线的V 投影（包括平面的正面迹线）。

②若一直线的H 面投影垂直平面内的水平线的H 面投影或平面的水平迹线，直线的V 面投影垂直于平面内的正平线的V 面投影或平面的正面迹线，则直线垂直于平面，如图4.22（b）所示。

图4.22　直线垂直平面

2）投影作图

（1）特殊情况：直线垂直于特殊位置平面

直线垂直于特殊位置平面，则直线一定是特殊位置直线，该平面具有积聚性的投影与其垂线的同面投影必然垂直。例如，与铅垂面垂直的直线一定是水平线，与正垂面垂直的直线一定是正平线，与侧垂面垂直的直线必是侧平线。简而言之，某投影面垂直面的垂线一定是该投影面的平行线。

【例4.10】过点K 作直线KL 垂直于平面P，如图4.23（a）所示。

【解】分析：已知平面P 为铅垂面，其H 面投影具有积聚性，则直线KL 的H 面投影垂直于该积聚性投影；又因为P ⊥H，KL⊥P，所以KL 一定是水平线。

作图：如图4.23（b）所示。

①过k 作kl⊥p（或PH），交p 于l；

②过k′作X 轴的平行线，与过l 的投影连线交于l′，直线KL 为所求垂线。

（2）一般情况：一般位置直线与平面垂直(www.xing528.com)

一般位置直线与一般位置平面垂直时，投影图中不能直接反映垂直关系。因此，无论作直线垂直于平面或作平面垂直于直线，还是判断直线与平面是否垂直的问题，都必须先作平面内的平行线，然后问题就归结为一般位置直线与平行线相垂直的问题，这时可以用直角投影定理在投影图中直接反映垂直关系。

【例4.11】过点K 作直线KL 垂直于△ABC，如图4.24（a）所示。

【解】分析：由图4.24 可知，△ABC 为一般位置平面，故其垂线也是一般位置直线。根据直线垂直于平面的投影特点，应首先作出平面内的水平线和正平线，然后作垂线。

作图：如图4.24（b）所示。

①过属于平面的已知点C、A 分别作属于平面的水平线CE 和正平线AD。

图4.23　直线与投影面垂直面相垂直

②过k 作kl 垂直于平面内的水平线的H 面投影ce，过k′作k′l′垂直于平面内正平线的V 面投影a′d′，所得直线KL 为所求的平面的垂线。

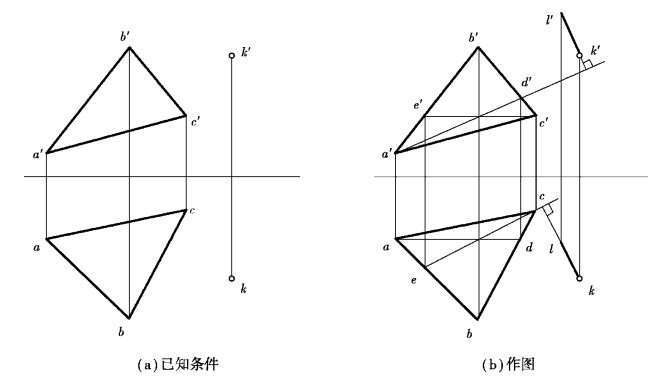
图4.24　过点K 作直线垂直于平面△ABC

【例4.12】判断已知直线MN 与△ABC 是否垂直，如图4.25（a）所示。

【解】分析：已知直线和平面均属一般位置，故应先作平面内的水平线和正平线，再检验已知直线是否同时垂直于所作水平线和正平线。若已知直线的H 面投影垂直于所作水平线的H面投影，同时已知直线的V 面投影垂直于所作正平线的V 面投影，则直线与平面垂直；否则，不垂直。

作图：如图4.25（b）所示。

①过点A 作属于△ABC 的水平线AD，过点C 作属于△ABC 的正平线CE。

②检验已知直线MN 是否垂直于水平线AD 和正平线CE。作图表明，虽然mn⊥ad，但m′n′与c′e′不垂直，故直线MN 与△ABC 不垂直。

图4.25　判断已知直线MN 是否垂直于△ABC