土木工程制图-平面相交处理

两一般位置平面的投影均无积聚性，所以必须通过辅助手段才能求得其交线。可采用辅助面和三面共点的原理作交线。

1）线面交点法

两个一般位置平面的投影相互重叠，通常用线面交点法求交线。一平面图形的边线与另一平面的交点，是两平面的共有点，也是两平面交线上的点，只要求得两个这样的交点并连接它们，便可获得两平面的交线。可见，两个一般位置平面求交线是第4.2.3 节中一般位置直线与一般位置平面求交点的应用。

【例4.9】求△ABC 与△DEF 的交线，如图4.20（a）所示。

【解】分析：两个一般位置平面无积聚性可利用，由于它们的投影重叠，可采用线面交点法。选作辅助面的边，首先剔除投影不重叠的边（如AC、BC、DE），因为这样的边在有限的长度下不与另外一个平面相交。在BC、DE、DF 中选两个，并尽量选择与另一图形重叠范围较多的边来作辅助面。

作图：如图4.20 所示。

①求交线KG。包含直线DF 作一个辅助正垂面P，P 与△ABC 的交线为MN，求MN 与直线DF 的交点K，得交线的一个点；同时包含EF 作一辅助铅垂面Q，求出Q 与△ABC 的交线，此交线与直线EF 的交点是G，得交线的另一个点，如图4.20（b）所示。连接KG，得△ABC 与△DEF的交线，如图4.20（c）所示。

②判别可见性。判别V 面投影的可见性时，找任意一个V 面的重影点，如以a′b′和d′f′的交点开始，向下作投影连线可知，AB 上的点Ⅰ在DF 上的点Ⅱ正前方，则a′b′可见，d′k′与△a′b′c′重叠部分不可见。故以V 面投影k′g′为界，在△k′g′f′一侧，两平面投影重叠部分属于可见；而在k′g′e′d′一侧，可见性则与△k′g′f′侧相反。当然也可以利用“虚实相间性”来作图，d′k′侧不可见，为虚线。交点是可见与不可见的分界点，所以k′f′可见为实线，a′c′相应段不可见为虚线，顺次循环，回到可见性判别的起点k′。

判别H 面投影的可见性，方法与V 面投影的可见性判断一样，如图4.20（c）所示。

两平面相交的可见性判别，还可以利用第4.2.3 节中的方法加以简化。从图4.20（b）可知，DF、EF 分别与下行平面△ABC（标注编号得顺序回转方向相反）相交于K、G，故直线DF、EF的V、H 面投影在交点K、G 的两侧可见部分相反，所以只需判别一个投影的可见性即可推断另一投影的可见性。

③完成作图，如图4.20（d）所示。(www.xing528.com)

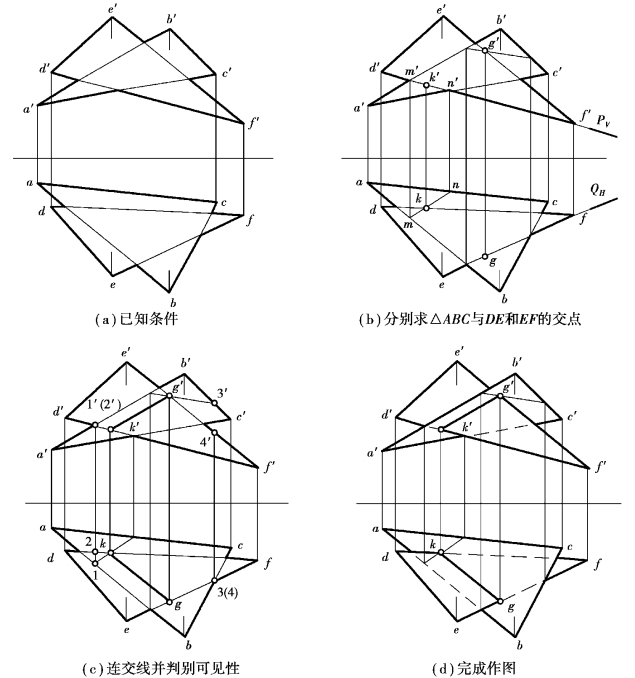
图4.20　线面交点法求两个一般位置平面的交线

2）线线交点法

线线交点法又称三面共点法。当相交两平面的投影图互不重叠时，其交线不会在两图形的有限范围内，此时可用三面共点原理，通过作辅助平面求其交线。如图4.21（a）所示，辅助平面R1 分别与已知平面P、Q 相交于直线ⅠⅡ、ⅢⅣ，这两条交线同属平面R1，故其延长线必然相交，交点K 一定属于P、Q 两平面的交线（K 同时属于R1、P、Q 三个平面）。同理，再利用平面R2可求得属于交线的另一点G，连接K、G 即得所求交线。

为便于作图，辅助平面一般都选特殊平面，尤其是平行平面。过已知点作辅助平面更为方便、准确。如图4.21（b）所示，三面共点法求交线的作图步骤如下：

①作水平面R1 的V 面迹线RⅣ，R1 与P（p′，p）、Q（q′，q）的交线（属于各平面的水平线）分别是ⅠⅡ（1′2′，12）、ⅢⅣ（3′4′，34），两者相交于点K（k′，k）。

②用同样的方法，作辅助平面R2 的V 面迹线R2V，得属于交线的又一交点G（g′，g）。注意：同一平面的水平线应相互平行。

③连接kg，k′g′。得两平面的交线KG。

此时，两相交平面投影图形相互不重叠，也就不需要判别可见性。

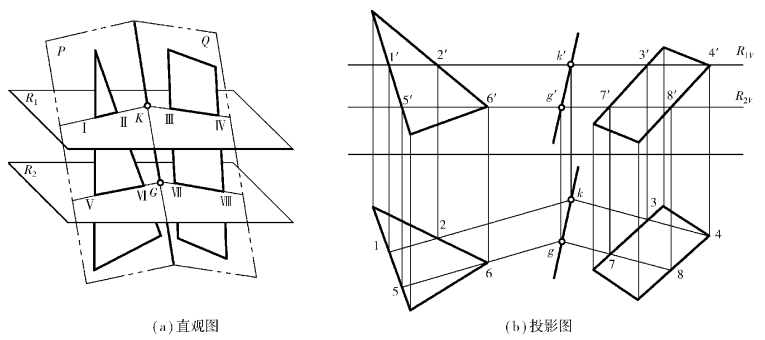
图4.21　三面共点法求交线