直线与平面相交的特殊情况是指直线或平面二者至少有一个对投影面处于特殊位置,即投影具有积聚性,那么交点同面投影一定在积聚性投影之上。此时可以根据交对的共有性在平面或直线上取点。
1)投影面垂直线与一般位置平面相交
由于直线投影积聚为一点,直线所有点的同面投影都在该点,当然也包括交点。交点是直线与平面的共有点,故交点也在平面上。利用直线的积聚性,得到交点的同面投影,再在平面上取点,作出此点的另一面投影。如图4.13(a)所示,直线MN 为正垂线,其V 面投影积聚成一点。MN 与△ABC 交点K 的V 面投影k′必然与之重合。过k′作属于△ABC 的任一辅助直线,并求其H 面投影与mn 的交点即可得k,如图4.13(b)所示。
作图步骤如下:
①求交点。
在V 面投影中过直线的积聚性投影作辅助直线AD 的V 面投影a′d′,在△ABC 求出AD 的H 面投影ad,与mn 相交于点k,如图4.13(b)所示。
②判别可见性。
利用重影点判别可见性,如图4.13(c)所示。因为直线MN 在V 面投影积聚为点,故V 面投影不必判别其可见性。在H 面投影中取直线MN 与平面边线AB 的重影点,并观察这两个点的V 面投影,直线MN 上的点Ⅰ就在平面边线AB 上的点Ⅱ正上方,故直线MN 的H 面投影nk段为可见。
在辨别可见性时所选择的重影点,必须选与已知直线交叉的平面上直线的点,同时要注意在V、H 面投影图上要一致,应为同一直线。如点Ⅱ即为AB 上的点,那么到另一个投影上去判别可见性时,必须保证仍然取的是直线AB 上该点的投影。
另一种判别可见性较为直接,就是直接对比投影中的位置关系。例如,需判别的是H 面投影的可见性,就是比较位置的上下问题,所以在V 面投影上去比较。a′b′在k′之下,故H 面投影中kn 可见。
③完成作图。
补全直线H 面投影,kn 段为可见(连成实线),km 段为不可见(将被△abc 遮住部分画成虚线),如图4.13(d)所示。
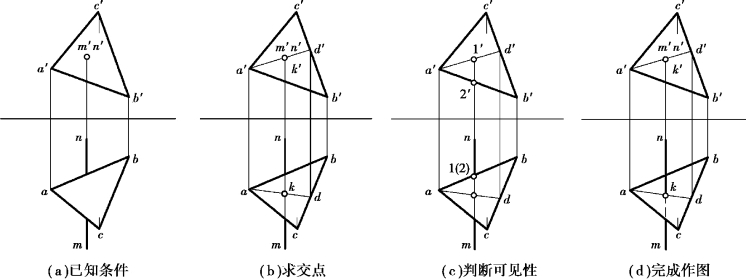
图4.13 正垂线与一般位置平面相交(https://www.xing528.com)
2)一般位置直线与特殊位置平面相交

特殊位置平面至少有一个投影具有积聚性,所以交点的同面投影就是平面的积聚投影和直线同面投影的交点。根据交点属于直线作出其另一投影,如图4.14 所示。为了更好地体现立体感,讨论相交问题时将平面视为不透明,直线被遮挡部分需要用虚线来表示,此时还需利用交叉两直线重影点来判别可见性。由图4.14可知,交点总是可见的,且交点是可见与不可见的分界点。
【例4.7】求直线MN 与铅垂面△ABC 的交点,并判别可见性,如图4.15(a)所示。

图4.14 一般位置直线与特殊位置平面交点画法分析
【解】分析:图中铅垂面△ABC 的H 面投影积聚为直线段abc,由于交点是平面与直线的共有点,故交点k 的H 面投影既在abc 上又在mn上,所以abc 和mn 的交点k 即为交点K 的H 面投影。
作图:
①求交点K。自abc 和mn 的交点k 向V 作投影连线与m′n′相交得k′即得交点K,如图4.15(b)所示
②判别可见性。利用重影点判别可见性,如图4.15(c)所示。△ABC 的H 投影积聚为直线,故不必判别其可见性;V 投影中m′n′与△a′b′c′相重叠的部分,则需要判别m′n′的可见性。对于直线MN 与△ABC 对V 面的重影点Ⅰ与点Ⅱ,点Ⅰ的H 投影1 在点Ⅱ的H 投影的前方,故k′n′段为可见,k′m′段与△a′b′c′重叠部分不可见,如4.15(d)所示。
另一种判别方法是利用平面的积聚性投影直接与直线进行位置对比。在H 投影上,以k 为界,kn 段在积聚性投影abc 的右前方,那么在V 投影上,k′n′可见,k′m′与△a′b′c′重叠的部分则不可见。

图4.15 求直线与铅垂面的交点
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




