平面直线与点-土木工程制图

1）属于一般位置平面的直线和点

（1）平面上的直线

由初等几何可知，一直线若过平面上的两点，则此直线属于该平面，如图3.46（a）中的M、N点在平面上，由这两点连成的直线MN 属于平面；或者一直线若过平面上的一点且平行于平面上的一条直线，此直线必在平面上，如图3.46（b）所示的直线KD，直线KD 过K 点，K 在平面P上，且KD∥AB，则直线KD 属于平面P；平面上的直线的迹点，一定在该平面上的同名迹线上。如图3.46（c）所示，M、N 点分别在QH、QV 两条迹线上，则直线MN 在平面Q 上。

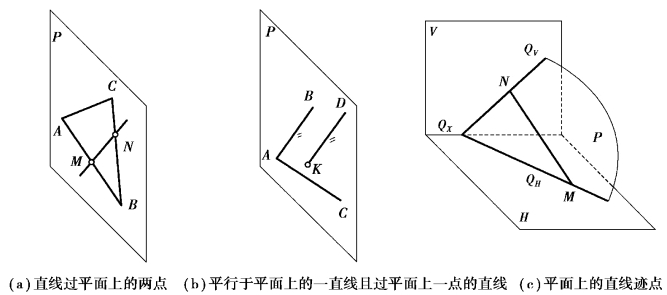
图3.46　平面上取线、取点的几何条件

【例3.14】已知相交两直线AB 与AC 的两面投影，在由该相交直线确定的平面上取属于该平面上的任意的一条直线（图3.47）。

【解】在直线AB 上取点D 及在直线BC 上取点E，即用直线上取点的投影特性求取，并将两点D、E 的同名投影以连接即得直线DE。

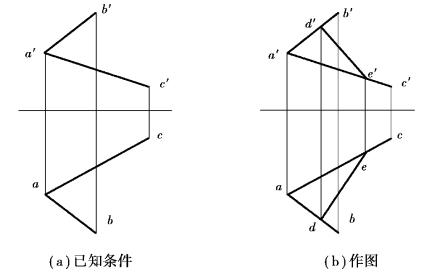
图3.47　取平面上的直线

（2）平面上的点

若点在平面上的一条直线上，则点在此平面上。平面上点的正投影，必在位于该平面上的直线的同名投影上。所以欲取平面内的点，必先在平面上取一直线，再在该直线上取点。反之，如果点在平面上，则点必在平面上的一直线上。

【例3.15】如图3.48（a）所示，已知△ABC 内一点M 的正面投影m′，求点M 的水平投影m。

【解】分析：在△ABC 内作一辅助直线，则M 点的两面投影必在此辅助直线的同名投影上。

作图： 如图3.48（b）所示。

①在△a′b′c′上过m′作辅助直线1′2′。

②在△abc 上求出此辅助直线的H 投影12。

③自m′向下作投影连线与辅助直线的H 投影的交点，即得点M 的H 投影m。

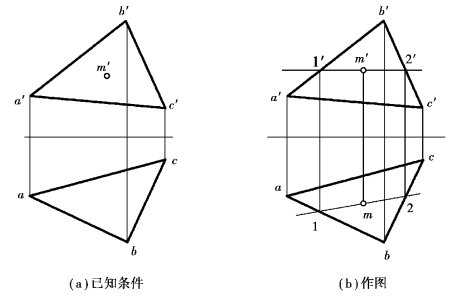
图3.48　平面上取点

【例3.16】已知平面四边形ABCD 的正面投影a′b′c′d′和边AD 的H 投影ad，边BC∥V 面，如图3.49（a）所示，请完成平面的H 投影abcd。

【解】分析：平面由不共线三点、两相交直线、两平行直线等来确定。已知平面上的一条正平线，那么可以过直线外一已知点再作一条与已知正平线平行的直线，即可确定平面。再用平面上取点的方法，完成平面余下各点的投影，将点的同名投影依顺序连接即可。

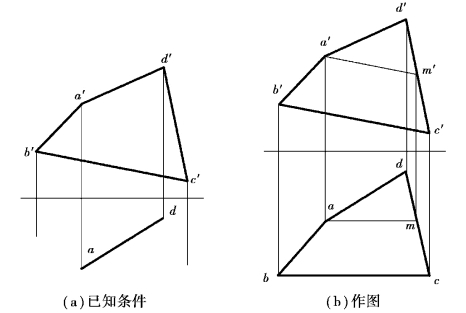
图3.49　完成平面的投影(www.xing528.com)

作图：①在四边形ABCD 的V 投影a′b′c′d′上过a′做a′m′∥b′c′交d′c′于m′，在H 上过a 做am∥OX 轴，交由V 投影中m′向下的投影连线于m。

②在H 上连接dm 并延长交由V 投影中c′向下的投影连线于c，求出dc。

③由于BC 为正平线，故在H 上过c 作bc∥OX 轴求出bc。

④连接ab，完成平面的H 投影abcd。

2）属于特殊位置平面的点和直线

属于特殊位置平面的点和直线，至少有一个投影重合于具有积聚性的迹线；反之，若直线或点重合于特殊位置平面的迹线，则点与直线属于该平面。

过一般位置直线总可以作投影面垂直面；过垂直线则可以作水平面[图3.50（b）]、侧平面[图3.50（c）]，以及无数多个正垂面[图3.50（d）]。

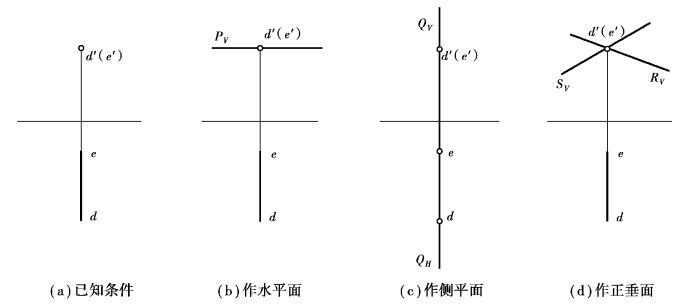
图3.50　过正垂线作平面

【例3.17】如图3.51（a）所示，已知一般线AB 的V、H 投影，包含直线AB 作投影面的垂直面。

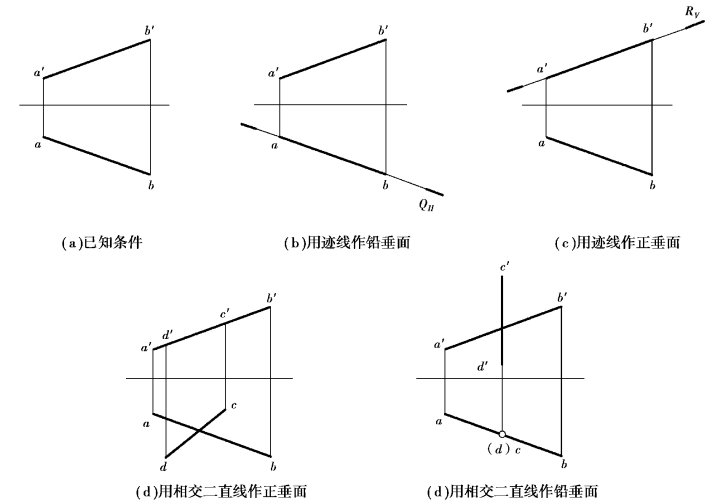
图3.51　过一般位置直线作特殊位置平面

【解】分析：若一般位置直线AB 属于某特殊位置平面，则该平面的迹线与直线的同名投影重合，由此可过直线AB 作出铅垂面或正垂面。

作图：①用迹线表示法作图：过ab 作一迹线QH 即为铅垂面，如图3.51（b）所示；过a′b′作一迹线RV 即为正垂面，如图3.51（c）所示。

②图3.51（d）、图3.51（e）是用几何元素表示法作出的正垂面及铅垂面，为了区别迹线与已知直线，在表示迹线平面时可用细线两端画粗线的方法来表示迹线，如图3.51（b）、（c）所示。

3）属于平面的投影面平行线

属于平面的投影面的平行线，不仅与所在平面有从属关系，而且还应符合投影面的平行线的投影特征，即在两面投影中，直线的其中一个投影必定平行于投影轴，同时在另一面的投影平行于该平面的同面迹线。

一般位置平面内的投影面的平行线同时有正平线、水平线及侧平线。

【例3.18】 已知△ABC 投影如图3.52（a）所示，过点A 作平面内的水平线及正平线。

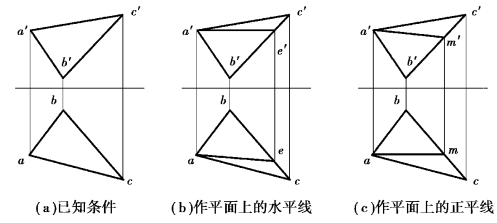
图3.52　作平面上的投影面平行线

【解】水平线V 投影平行于OX 轴，过点a′作平行于OX，与b′c′交于点e′，在bc 上作出e，连接ae 即为所求水平线，如图3.52（b）所示。类似求得正平线AM 如图3.52（c）所示，在这里叙述从略。