点的坐标值反映了点在投影体系中的左右、前后及上下的位置,而两点之间的相对位置,可以通过比较两点坐标值可知:x 值大,距投影面W 更远,在左方;y 值大,距投影面V 更远,在前方; z 值大,距投影面H 更远,在上方。如图3.10 中的A、B 两点,A 点在B 点的上、左、前方,也可以说B 点在A 点的下、右、后方。

图3.10 两点的相对位置
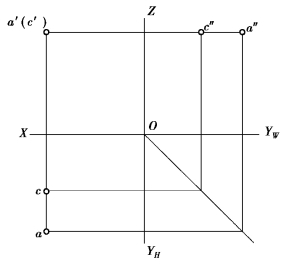
图3.11 V 面的重影点
如果两点处于一条投射线上,则两个点的投影在该投影面上重合,这两个点为该投影面的重影点。如图3.11 中,点A 在点C 的正前方,则A、C 两点在V 投影重合,A、C 两点称为V 面的重影点。同理,如两个点为H 面的重影点,则两点的相对位置是正上(下)方;如两个点为W 面的重影点,则两点的相对位置是正左(右)方。在第一分角,由于投射线总是由远向投影面进行投射的,因此对于重影点,就有一个可见性的问题。如图3.11 中,点A 在点C 的正前方,a′可见,c′不可见。为了表示可见性,在不可见投影的符号上加上括号( ),如(c′)。判别可见性的原则是:前可见后不可见、上可见下不可见、左可见右不可见。总的说来,是坐标值大的、相对于两点来说距投影面远的,为可见。从直角坐标关系来看,重影点间实际上是有两组坐标相等,如图3.11 中A、C 两点的X、Z 坐标相等,只有在Y 方向点A 大于点C。
【例3.4】已知点A(10,10,20);点B 距W 面、V 面、H 面的距离分别为20,5,10;点C 在A 点的正下方10,求A、B、C 三点的投影并判别可见性。(https://www.xing528.com)
【解】分析:点A 以坐标大小、点B 以距投影面距离、点C以两点之间的相对位置确定空间位置。
作图:如图3.12 所示。
①由点A 的坐标求出点A 的三面投影。
②根据点B 相对于投影面的距离,实际上是给出了点B的坐标,求出B 点的三面投影。
③根据点C 在点A 的正下方,求出点C 的三面投影,A、C两点为H 面的重影点。
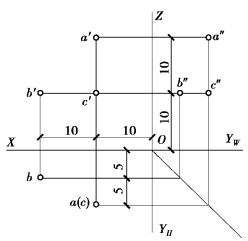
图3.12 作点的三面投影
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




