土木工程制图：两面投影体系与三面投影体系中的投影

根据初等数学的概念可知，两个坐标不能确定空间点的位置。因此，点在一个投影面上的投影，可以对应无数的空间点。为了确定点的空间位置，设置两个互相垂直的正立投影面V 和水平投影面H（图3.1），这两个投影面将空间划分为4 个区域，每个区域即为一分角，面对X 轴的左端，按逆时针的顺序为第Ⅰ、Ⅱ、Ⅲ、Ⅳ分角。

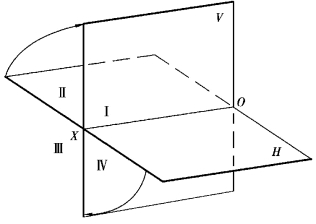
图3.1　相互垂直的两投影面

1）点的两面投影

根据我国工程制图标准的规定“形体的图样，应按平行正投影法绘制，并采用第Ⅰ分角画法”，故将讨论重点放在第Ⅰ分角中投影的画法。

如图3.2（a）所示，过点A 分别向V 面、H 面作投射线，得到与V 面、H 面的垂足a′、a。a′ 称为空间点A 的正面投影，简称V 投影，其坐标是（x，z），反映点A 的左右上下位置；a 称为空间点A 的水平投影，简称H 投影，其坐标可用（x，y）表示，反映点A 的左右前后位置。空间点A 及其投影a′、 a 构成的平面与OX 轴的交点称为ax。由此可见，可以通过点A 的V 投影和H 投影反映空间点A 的坐标（x，y，z）。

前面所描述的点以及投影仍然是在三维空间中，而图纸是二维空间（即平面），若将V、H 面投影体系如图3.2（a）所示展开，即得到空间点A 的V、H 两面投影图，如图3.2（b）所示。去掉投影面的边框，就得到点A 的V、H 两面投影图，如图3.2（c）所示。

（1）点的两面投影特性

从图3.2（a）中可知，Aa 丄H 面，Aa′丄V 面，则平面Aa′axa 同时垂直于H、V 面和投影轴OX。展开后的投影图上，a 和a′的投影连线垂直于OX，即aa′丄OX。由于Aa′axa 是个矩形，aax =Aa′=y，a′ax =Aa=z。由此可以得到点在V/H 两面投影体系中的投影特性为：

①点的V 投影和H 投影的连线，垂直于投影轴OX 轴（aa′丄OX）；

②点的投影到投影轴OX 的距离等于空间点到共投影轴的另一投影面的距离（a′ax =Aa =z，aax =Aa′=y），如图3.2 所示。

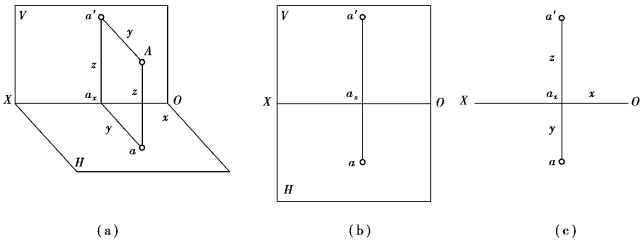
图3.2　点的两面投影

以上投影特性也适合于其他分角中的点。

规定：在投影图中，将连接点的相邻两面的投影的直线称为投影连线。

（2）点在其他分角中的投影

在实际的工程制图中，通常都把空间形体放在第一分角中进行投影，但在画法几何学中应用图解法时，常常会遇到需要把线或面等几何要素延伸的情况，故此很难使它们始终都在第一分角内。这里简单地介绍点在其他分角的投影情况。

如图3.3 所示的是点在第Ⅰ、Ⅱ、Ⅲ、Ⅳ分角的投影情况。投影的原理以及投影特性与前面所讲述的点在第一分角的投影完全一样，投影面的展开与前面所讲的一样，得到的两面投影图对于各分角的点的区别如下：点A 在第Ⅰ分角中，其V 投影和H 投影分别在OX 轴的上方和下方；点B 是在第Ⅱ分角中的点，其V 投影和H 投影均在OX 轴的上方；点D 在第Ⅲ分角中，V 投影在OX 轴的下方，H 投影在OX 轴的上方，其情况与第Ⅰ分角正好相反；而第四分角的点C，两个投影均在OX 轴的下方，则与第Ⅱ分角的点B 相反。显然，在Ⅱ、Ⅳ分角内，两个投影均在投影轴一侧，对于清晰地表达形体是不利的。因此，ISO 标准、我国和一些东欧国家多采用第Ⅰ分角投影的制图标准，美国、英国以及一些西欧国家采用了第Ⅲ分角投影制图标准。

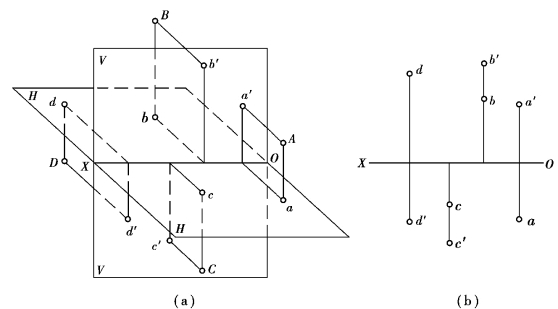
图3.3　点在4 个分角中的投影

（3）特殊位置点的投影

所谓的特殊位置点，就是点在投影面上或在投影轴上的点。

从点的投影原理可以看出，属于投影面上的点，其坐标值至少有一个为零，则有一个投影与它本身重合，而另一个投影在投影轴上，如图3.4 中的A、B、D、E 点。其中点A、E 均在H 面上，则其V 投影在OX 轴上（a′、e′在OX 轴上），点A 在前半H 面上，其H 投影a 在OX 轴的下方，E点在后半H 面上，则其H 投影e 在OX 轴的上方；点B、D 均在V 面上，则其H 投影在OX 轴上（b、d 在OX 轴上），而由于两者所处的上下位置不同，V 投影b′在OX 轴的上方，V 投影d′在OX轴的下方。

属于投影轴的点C，其V、H 两个投影都在投影轴OX 轴上，并与该点重合，如图3.4 所示。

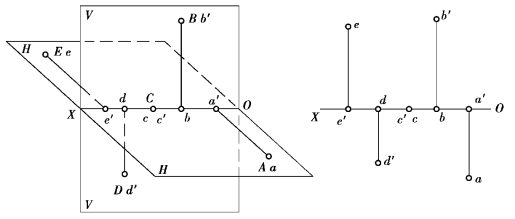
图3.4　4 个分角中特殊点的投影

2）点的三面投影

虽然两面投影已经可以确定空间点的位置，但如第1 章中所述，在表达有些形体时用两面投影不能表达清楚，解决之道就是设置第三个投影面。

如图3.5（a）所示，由空间点A 分别向V、H、W 面进行投影，得到点A 在各投影面上的投影a、a′、a″。其中a″是空间点A 的W 投影。投射线Aa、Aa′、Aa′′两两组合得3 个平面：aAa′、aAa″和a′Aa″，这3 个平面与投影轴OX、OY 和OZ 分别相交于ax、ay、az。这些点和原点O 及其投影a、a′、a″的连线组成一个长方体，如图3.5（a）所示。

为了把3 个投影a、a′、a″表示在一个平面上，将三面投影体系展开后就得到了点A 的三面投影图，如图3.5（b）所示，去掉投影面边界得到图3.5（c）。

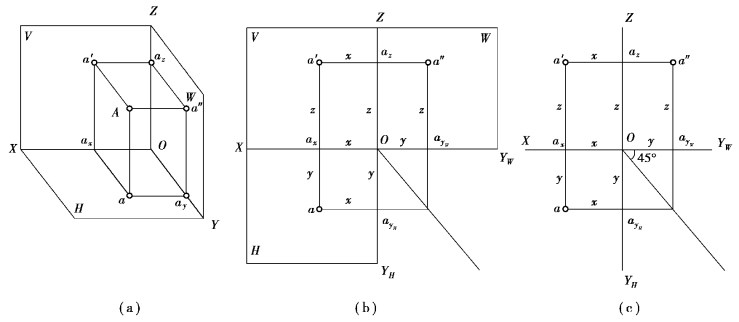
图3.5　点在三面投影体系中的投影(www.xing528.com)

点的三面投影特性如下：

①点的投影连线垂直于投影轴：a′a 丄OX、a′a″丄OZ 、aayH丄OYH、a″ayW丄OYW。

②点的投影到投影轴的距离，等于空间点到共投影轴的另一投影面的距离，即：

点A 到H 面的距离Aa=a′ax =a″ay =azO=z，即高平齐；

点A 到V 面的距离Aa′=a″az =aax =ayO=y，即宽相等；

点A 到W 面的距离Aa″=a ay =a′az =axO=x，即长对正。

点的这两条投影特性，称为三面投影的投影规律，也常称为“三等关系”（长对正、高平齐、宽相等）。这也说明，在三面投影体系中，任两个投影都有内在的联系，它们共用一个投影轴。只要给出一个点的任意两个投影，就可以求出其第三个投影。图3.5（c）中的45°线就是为了保证“宽相等”而作的辅助线，也可用四分之一圆来代替。

【例3.1】如图3.6 所示，已知空间点B 的H 投影b 和V 投影b′，求该点的W 面投影b″。

图3.6　已知点的V、H 投影求W 投影

【解】做题过程就是一个应用“三等关系”的过程，作法如图3.6（b）中的箭头所示。

①根据本题已知b′和b（长对正），过b′引OZ 轴的垂线b′bz 交bz 后适当延长（高平齐）。

②过b 引OYH 轴的垂线bby 交所作45°辅助线后再引OYW 轴的垂线交第①步所作高平齐的线于b″（宽相等），b″即为所求。

【例3.2】如图3.7 所示，已知点C 的V 投影c′和W 投影c″，求点C 的H 投影c。

【解】作法如图3.6（b）中的箭头所示。

①根据本题已知c′和c″（高平齐），过c′引OZ 轴的垂线c′cx 交cx 后适当延长（长对正）。

②过c″引OYW 轴的垂线c″cy 交所作45°辅助线后再引OYH 轴的垂线交第①步所作长对正的线于c（宽相等），c 即为所求。

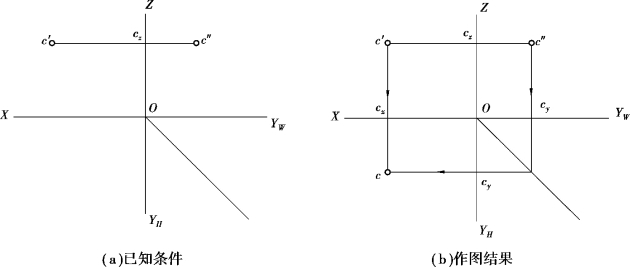
图3.7　已知点的V、W 投影，求其H 投影

【例3.3】已知空间点A 的坐标为：x =15 mm、y =10 mm、z =20 mm，试作出点A 的三面投影图。

【解】①在图纸上作一条水平线和铅垂线，两线交点为坐标原点O，其左为X 轴，上为Z 轴，右为YW，下为YH。

②在X 轴上取Oax =15 mm；过aX 点作OX 轴的垂线，在这条垂线上自ax 向下截取aay =10 mm 和向上截取a′az =20 mm，得H 投影a 和V 投影a′，如图3.8（a）、（b）所示。

③由a′向OZ 轴引垂线，在所引垂线上截取a″az =10 mm，得W 投影a″，如图3.8（c）所示。这一步也可按【例3.1】方法，根据“三等关系”作图得到。

图3.8　已知空间点的坐标，求其三面投影

当空间点在投影面上时，则点的坐标至少有一个为零。如图3.9 所示，空间点D 在H 面上，则z=0，因此，点D 的V 面、W 面投影分别在OX 轴和OYW轴上（d′在OX 轴上，d″在OYW 轴上），而H 面的投影（即d″）与空间D 点本身重合。此时应注意，d″必须在OYW 上，这是因为d″是点D 在W 面上的投影。

图3.9　属于投影面的点

结合点的坐标来看，特殊点具有以下特点：

①属于投影面上的点，其坐标值必有一个为零，它的一个投影与它本身重合，而另两个投影在与该投影面有关的两个投影轴上。

②属于投影轴上的点，其坐标值必有两个为零，它的两个投影都在此投影轴上，并与该点重合，而另一投影在原点。

③当点在原点时，其坐标值均为零，三个投影都在原点处。