大学生电动方程式赛车设计-轮胎模型

1.轮胎坐标系

为了方便研究人员分析轮胎的力学特性，SAE建立了标准的轮胎坐标系。如图12－12所示，车轮平面与车轮旋转轴线相垂直，且处于轮胎中分面上。坐标系的原点O为轮胎接地轨迹的中心。轮胎坐标系的x轴定义为地平面与车轮平面的交线，规定沿着车轮行驶方向为正。z轴垂直于地面，规定指向上方为正。y轴为车轮旋转轴线在地平面上的投影线，规定指向左方为正。

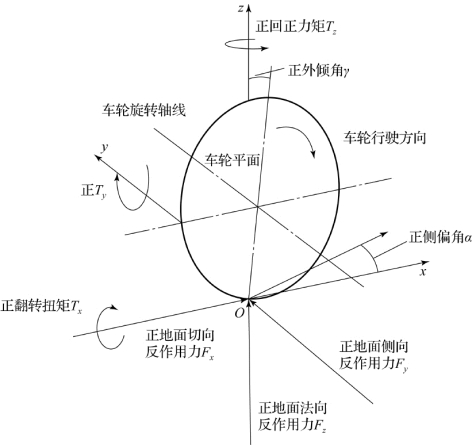
图12－12　轮胎坐标系

2.轮胎运动参数

在赛车加速和减速时，赛车前后轴的载荷会发生转移，考虑到纵向和侧向加速度的综合作用，车轮的垂直载荷可以表示为

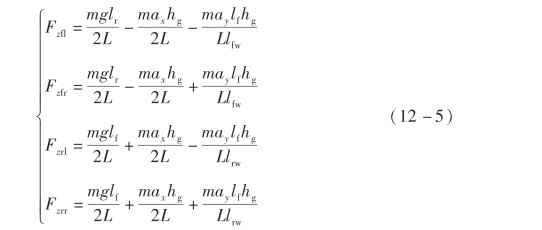
各车轮的轮胎侧偏角可以由下式计算，即

对应的车轮轮心速度为

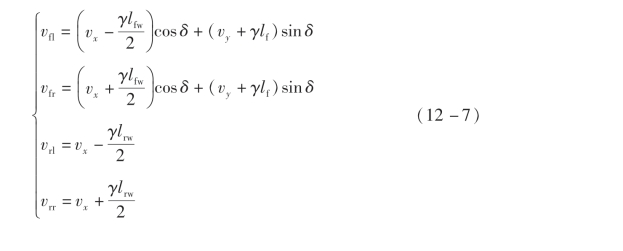
式中，L为轴距；lf、lr分别为车辆的质心到前轴的距离、质心到后轴的距离；ax为车辆的纵向加速度；ay为车辆的侧向加速度；αi为各个车轮的轮胎侧偏角；hg为车辆的质心高度；vi为各个车轮的轮边速度，由轮速计算得到。

3.魔术公式轮胎模型

图12－13所示为赛车所用轮胎试验数据拟合的侧偏特性图，当轮胎的侧偏角都比较小时，此时轮胎的侧偏角与轮胎的侧偏力呈线性关系；但是当轮胎的侧偏角比较大时，此时车辆处于非线性状态，线性区域内的表达式无法准确表示轮胎在非线性区域的特性，需要一个能同时适用于线性区域和非线性区域的轮胎模型来得到轮胎的纵向力Fx和轮胎的侧向力Fy，且试验数据只有在特定轮胎法向载荷下的轮胎侧偏特性，为了扩展其使用范围，因此考虑采用轮胎模型。

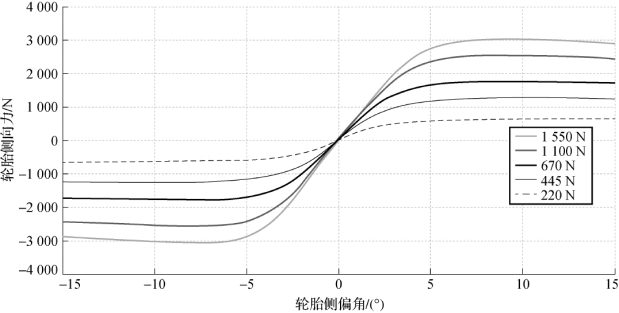
图12－13　试验数据拟合的轮胎侧偏特性

魔术轮胎模型是一种经验模型，其可以根据试验数据拟合出公式系数，即便在试验数据范围外也能使用该轮胎模型。

若在纵向力或者侧向力中只产生了一个力，此时魔术轮胎模型的表示形式为

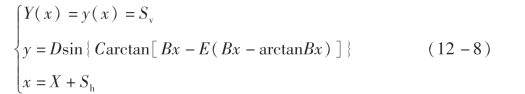(www.xing528.com)

式中，Y在纯制动工况下为轮胎纵向力Fx，在纯转向工况下为轮胎侧向力Fy；x为轮胎的侧偏角或者车轮的纵向滑移率；B、C、D、E为轮胎模型的参数因子；Sv为地面法向变形；Sh为水平变形；X在纵向力计算时是纵向滑移率，在侧向力和回正力矩计算时是侧偏角。

只考虑车辆的纯转向工况，可以用式（12－9）表示轮胎的侧向力Fy0、轮胎侧偏角α和车轮法向载荷Fz之间的关系，即

表12－1　转向工况下拟合参数

只考虑纯制动工况，可用式（12－10）表示轮胎纵向力Fx0、车轮的纵向滑移率λ和轮胎法向载荷Fz之间的关系为

表12－2　纯制动工况下拟合参数

但是车辆会在转向和制动共同存在的工况下行驶，此时轮胎的纵向力Fx、轮胎的侧向力Fy与轮胎的侧偏角α、纵向滑移率λ之间的关系如下。

纵向力为

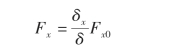
侧向力为

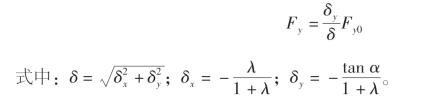
在进行汽车操纵稳定性研究时，轮胎的侧偏特性是一个非常重要的影响因素，因此本书主要分析魔术轮胎模型的侧偏特性。赛车在行驶时，轮胎的垂向载荷在400～800 N范围，因此可以分别选取垂直载荷为400 N、600 N、800 N，对所拟合的魔术轮胎模型进行分析，仿真结果如图12－14所示。

图12－14　不同载荷下魔术轮胎模型侧偏特性

由不同载荷下魔术轮胎模型的侧偏特性曲线可知，当轮胎侧偏角在0°～5°范围内时，轮胎基本处于线性区域内；当轮胎侧偏角大于5°时，随着轮胎侧偏角的增大，轮胎的侧向力略有下降。同时，所建立的魔术轮胎模型将已有特定法向载荷下的轮胎试验数据加以延伸，能够用于分析不同载荷下的轮胎侧偏特性，计算出不同工况下的轮胎力，作为后面稳定性控制系统的输入。