物体在流场中的受力现象可以使用伯努利方程加以解释。伯努利方程由瑞士物理学家丹尼尔·伯努利于1738年提出,描述流体沿着一条稳定、非黏性、不可压缩流线的移动行为。首先,对于赛车流场而言,除了散热风扇及轮胎外,其余部件相对于来流都是匀速直线运动,因此对于前翼、尾翼、扩散器等空气动力学套件,其周围流场可以近似认为稳定。其次,实际流体存在黏性,而物体表面附近的区域流体黏性力占据很大比例,称之为边界层。因此,边界层之外,伯努利定理才可用于定性分析流场。再次,运动速度在马赫数0.3以下的物体,周围流场的密度变化不超过10%,工程研究时可以近似认为是不可压缩流动。对于大学生方程式赛车而言,最高速度也远远低于马赫数0.3,因此其周围流场可以认为是不可压缩的。
伯努利方程由能量守恒定理推导而来。其假设在稳态流动中,同一流线上各点的能量相同。而能量包括动能、势能和内能。最终的方程形式为
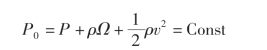
式中,P、ρ、v分别为流体的压强、密度和速度;Ω为铅垂高度h与重力加速度g的乘积。在空气动力学分析中,ρ与Ω的乘积变化较小,可以近似忽略,因而方程转化为

根据伯努利方程,可以解释为何翼型能够产生升力。对于飞机而言,升力主要来自上翼面。翼型的上半部分通过其特殊形状,使得从其上方流过的空气在翼型前段处于较大的顺压梯度中,因此流速得以提升。根据伯努利方程,流速的提高使得动压升高,静压因此减小,产生的“吸力”使得飞机获得升力。对于赛车而言,将原有的翼型倒置,依靠前翼、尾翼等的下翼面流速增加,产生需要的下压力。
对于机翼附近的绕流使用点涡进行近似,加上库塔条件,薄翼型在不考虑黏性时可以直接求解翼型升力,结果为
![]()
式中,CL为无量纲形式的升力系数;α为翼型的弦线与来流的夹角,即迎角,单位为rad。对于薄翼型低迎角的情形,该结果与试验结果基本一致。然而,试验也表明,升力系数并不会完全随着迎角的增大而不断增加,这是由于实际流体的黏性造成的。边界层中,物体壁面处的流体流速为0,并随着离壁面的距离增加而不断接近无黏时当地速度。平板表面的边界层(层流)厚度发展及速度型分布见图8-1。(https://www.xing528.com)
在飞机翼型的上表面,气流在前段受到顺压梯度加速之后,在后段会受到逆压梯度减速。由于边界层中的气流相较边界层外的气流速度低,因此受到该减速时更加容易出现局部的气流逆流(图8-2),因而发展为翼型的失速,即气流不再附着于翼面,而翼型也因此失去升力(图8-3)。
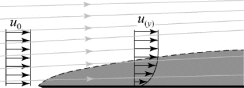
图8-1 边界层图解

图8-2 失速现象
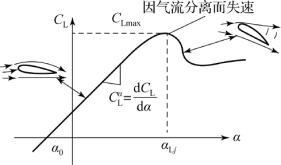
图8-3 升力系数和斜率的关系
赛车的翼片安装类似于将飞机的翼片倒置,因此可以得出结论,赛车翼片产生的下压力与翼型的选择及其迎角有关。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




