阿克曼转向梯形的原理和应用

为了避免在汽车转向时产生路面对汽车行驶的附加阻力和轮胎过快磨损，要求转向系统能保证在汽车转向时，所有车轮均做纯滚动。显然，这只有在所有车轮的轴线都相交于一点时方能实现，如图4－6所示。此交点O称为转向中心，前轴内外车轮转角需要满足式（4－6），即

1818年，英国人鲁道夫·阿克曼为一种转向梯形申请了专利。转向梯形由前轴、转向节臂与转向横拉杆组成，被称为阿克曼梯形。这种结构可以使外侧车轮转角小于内侧车轮转角，当时广泛应用在马车上。由于横拉杆是一根长杆，且这种梯形属于整体式转向梯形，故一侧车轮的跳动会直接影响另一侧，如图4－7所示。

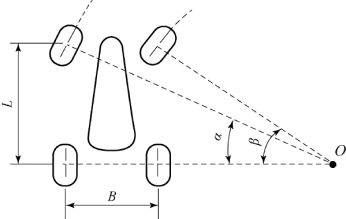
图4－6　双轴汽车转向时理想的两侧转向轮偏转角的关系

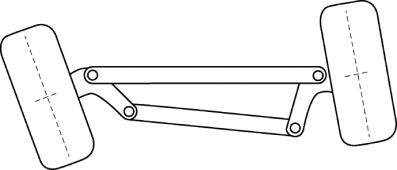
图4－7　整体式转向梯形

随着独立悬架的发展，整根的前轴没有了，转向横拉杆也被断成左、右两根，这就是断开式转向梯形，FSAE赛车基本均采用这种梯形，如图4－8所示。

图4－8　断开式转向梯形(www.xing528.com)

如今的阿克曼转向几何有3种，即正阿克曼、平行阿克曼与反阿克曼，如图4－9所示。正阿克曼指的是外侧车轮转角小于内侧；平行阿克曼指的是外侧车轮转角等于内侧；反阿克曼指的是外侧车轮转角大于内侧。

图4－9　阿克曼转向几何类型

（a）正阿克曼；（b）平行阿克曼；（c）反阿克曼

图4－10　考虑轮胎侧偏的阿克曼转向

赛车过弯时侧向力很大，轮胎侧偏现象很明显，这导致阿克曼梯形在赛车上发生了变化。在图4－10中，不考虑轮胎侧偏时，转向瞬心为I；如果考虑轮胎侧偏，后轮会因为轮胎侧偏角的存在而使转向瞬心I提前到X位置。这时，若前轮侧偏角与后轮相当，且左、右两轮侧偏角相等，那么为了使四轮做纯滚动，两个前轮实际转角趋于相等，也就是平行阿克曼。由于转弯时的轮荷转移，外侧轮胎往往有更大的侧偏角，那么为了使四轮做纯滚动，外侧车轮转角反倒要大于内侧车轮转角，也就是反阿克曼。部分现代赛车为了弥补转弯时的侧偏角，采用了平行阿克曼甚至反阿克曼转向。

为了表示转向系统的阿克曼程度，定义了阿克曼率（Ackermann Percentage），即

阿克曼率为正即正阿克曼，为零即平行阿克曼，为负则为负阿克曼。FSAE赛车阿克曼率取值为0～70%。确定赛车阿克曼率的两种路线：一种是理论派，即基于轮胎数据，以转弯时最大的侧向力为设计目标，综合考虑轮荷转移、侧偏角、车轮外倾角等迭代求解出阿克曼率；另一种是实战派，即认为理论不能完全模拟现实各种因素的影响，如轮胎温度。实战派推崇设计出阿克曼率可变的转向梯形，在实车调试时直接比较。通常这是由转向横拉杆外点设计为可调实现的。