可展开表面的展开:平行线、放射线、三角形等方法

可展开表面的展开常用的方法有平行线展开法、放射线展开法、三角形展开法等。

（一）平行线展开法

如果形体的表面是由一组互相平行的直素线或棱线构成的（如各种棱柱体、圆柱体、圆柱曲面等），其表面的展开可以用平行线法。

1.平行线展开法的基本原理

平行线法的展开原理，是将零件的表面看作由无数条相互平行的素线组成，两相邻素线及其上下两端线所围成的微小面积可近似地看作是梯形或长方形，当分成的面积较多时，各小平面面积的和就等于形体的表面面积。只要将每一小平面的真实大小，按照原来的分割顺序和上下位置不遗漏不重叠地依次画在平面上，就得到了零件表面的展开图。

2.直角弯管的展开画法

直角弯管是由两个相同的圆柱体组成的，其展开如图4-69所示。

图4-69　直角弯管的展开

在展开画线时，仅画出一部分即可。其步骤是：

（1）按弯管尺寸要求作投影图的主视图和俯视图（按国家制图标准，允许只画半个圆）。

（2）把主视图的投影线AB、AD、BC表示出来。

（3）等分俯视图半圆周为4或8等分，得出各等分点为1、2、3、4、5或1、2、3……8、9。

（4）通过各等分点向上作垂直线，交于CD线上，分别得到相应各点1、2、3、4、5或1、2、3……8、9。

（5）延长AB线，在AB延线上截取EF线段，其长度等于圆管的周长，若俯视图是半圆时，其等分为二倍的俯视图等分；若俯视图是全圆，则其等分为俯视图同样等分，然后将其各等分点逐次标明号数。

（6）在EF线上各等分点向上引垂线并与主视图CD线上各点向右引出的水平线对应相交，得出各交点。

（7）最后，把这些交点用曲线板连成一条光滑的曲线，即画出所求的展开图。

不论弯管的直径长短和所弯的角度大小，展开图形都可以用上述方法作出。展开图形画好后，若要求进行咬接，则应按咬缝宽度加上咬边尺寸画。

3.三通管的展开画法

三通管在管子连接上应用很广。这种管子的接头由主管1和支管2两部分组成，如图4-70所示，它的展开步骤如下：

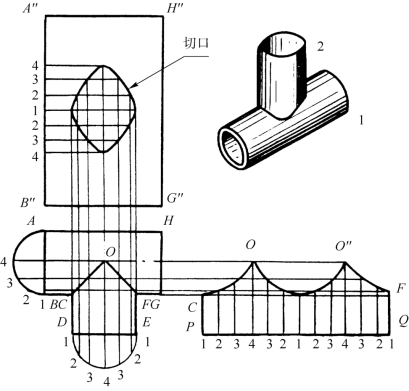
图4-70　三通管的展开

（1）按照实际尺寸画出主管和支管的俯视图ABCDEFGH，主管右视图半圆周A-4-B和支管俯视图半圆周D-4-E。把支管的俯视图半圆周D-4-E 6等分，等分点为1、2、3、4、3、2、1，由等分点向上引垂直线，把主管右视图半圆周的1/2（即4B）分成3等分，等分点为1、2、3、4，由等分点向右引水平线。

（2）延长DE线，取PQ等于圆周长度并分成12等分（因半圆周分6等分）。等分点为1、2、3、4、3、2、1、2、3、4、3、2、1。由各等分点向上作PQ的垂直线，与由主管右视图4-B各等分点向右引出的水平线对应相交，把各交点用曲线板连成圆滑曲线，即可得到支管的展开图CPQFQ″O。

（3）延长BA线和GH线，A″B″和H″G″线段等于主管圆周长度的长度并用圆规量取主管右视图1/2半圆周4-B各等分点的长度，在A″B″线段中点1分别向上、向下作等分点2、3、4，再由各等分点向右作A″B″的垂直线，与支管俯视图半圆周D-4-E各等分点向上引出的垂直线对应相交。把各交点连成曲线，即为接口的展开图，把它挖去即得出主管的展开图

B″A″H″G″。

不论三通管直径大小，和两管相交成什么角度，只要正确画出主视图和俯视图，都可运用上述方法画出它的展开图形。

4.斜口正圆柱管的展开

图4-71（a）为斜口正圆柱管的立体图，图4-71（b）是它的投影图和展开图的作图过程。斜口正圆柱管的表面也是正圆柱表面，不过斜口圆柱管表面上的素线长度不一。为此，可在管面上取若干素线，将圆柱面视为棱柱面，即可将其展开，具体展开过程简述如下：

（1）在水平投影上将下口12等分，得12个点，并分别过等分点作主视图底口垂线交斜口于1″、2″、3″、4″、5″、6″、7″。

图4-71　斜口正圆柱管的展开

（a）斜口正圆柱管的立体图；（b）斜口正圆柱管的投影图和展开图的作图过程

（2）作下口底边的延长线并在延长线上截取线段12段，使每段均等于水平投影的已等分弧长，得12个交点。

（3）分别过12个点作底边延长线的垂线。

（4）过1″、2″、3″、4″、5″、6″、7″分别作底边的平行线，与12个点的垂线相交于12个点Ⅰ、Ⅱ、Ⅲ、Ⅳ、Ⅴ、Ⅵ、Ⅶ……

（5）用曲线板把12个交点光滑地连接起来即得到斜口正圆柱管的展开图。展开图上左右两端素线I-I是接缝线。

需要说明的是这种近似展开法，其断面图等分点越多，展开越精确。

5.平行线展开法小结

从以上几例展开的情况可以看出，只有当柱状形体的所有彼此平行的素线都平行于某个投影面时，平行线展开法才可应用。

平行线展开法的作图步骤可归纳如下：

（1）任意等分断面图（或任意分割断面图），由分点向对应视图引投影线（即素线投影线），在该视图上得一系列交点，也就是由断面图上的分点确定形体上相应的素线位置和素线长度。

（2）在与该视图素线垂直的方向上截取一线段，使其长度等于正断面周长，且在此线段上照录断面图上各分点，再过各照录点引垂直线，与该视图中在第一步时所得交点而引的一组水平线同名各点对应相交。

（3）将交点依次连接，完成展开图。

在平行线展开图中所说的断面图是正断面图，也就是和彼此素线都垂直的断面图。在展开图中，断面图伸直后所在的线段称为展开图的长度，展开图上的曲线称为展开曲线。与展开长度垂直的直线和展开曲线必有交点，此交点到展开长度所在线段的距离称为展开图的高度。

（二）放射线展开法

放射线展开法适用于零件表面的素线相交于一点的形体（如圆锥、椭圆锥、棱锥等）表面的展开。

1.放射线展开法的基本原理

放射线法的展开原理是将零件表面由锥顶起作出一系列放射线（即素线或棱线），与底边线一起，将锥面分成一系列近似的小三角形，每个小三角形作为一个平面，将各三角形依次展开画在平面上，就得出所求的展开图。放射线展开法的关键是确定这些放射线的长度和相邻放射线间的夹角。

现以正圆锥管为例说明放射线展开法的基本原理，正圆锥的特点是锥顶到底圆任一点的距离都相等，所以正圆锥管展开后的图形为一扇形，如图4-72（a）所示，它的展开图可通过计算或作图求得。如图4-72（b）和图4-72（c）所示，展开图的扇形半径等于圆锥素线的长度。扇形的弧长等于圆锥底圆的周长πd，扇形中心角α=360πd/（2πR）=180d/R。

圆锥面也可视为由正棱锥面底面的边数无限增多而形成的。圆锥面的展开变成棱锥面的展开，即可用放射法作图。用这种方法作图虽有一定误差，但可通过增加圆周等分数的方式将误差控制在允许范围内。

图4-72　正圆锥管的展开

（a）正圆锥管展开为扇形；（b）扇形半径与圆锥素线的关系；（c）扇形弧长与圆锥底圆周长的关系

用作图法画正圆锥管的展开图时，将底圆周等分并向主视图作投影，再将各点与顶点连接，即将圆锥面划分成若干三角形，以O′为圆心，O′-1′为半径作圆弧，在圆弧上量取圆锥底圆的周长便得到展开图。

2.正四棱锥的展开画法

正四棱锥的侧面是由四个全等的等腰三角形所围成，画展开图需要依次作出四个等腰三角形的实形。正四棱锥的左、右侧面是正垂面，前、后侧面为侧垂面，在主、俯视图找不到实形。底面正四边形边是水平线，水平投影为实长；四个侧棱相等并交会于一点，是一般位置线，主、俯视图找不到实长，因此，求作其展开图的关键是求得棱线的实长。(www.xing528.com)

（1）作出主视图，使直线AB等于正方形底面的边长。作俯视图，使直线A1 B1平行于直线AB，并使两线等长。作出正方形A1 B1A2B2，如图4-73所示。

（2）在俯视图上通过点O作直线O-6平行于直线A2 B2，再以O点为圆心，OB2之长为半径作圆弧交O-6得点7，自点7作O-6的垂线，它在AB的延长线上相交1点。作出直线C-1，即为棱线实长。

图4-73　正四棱锥的展开

（3）以顶点C为圆心，C-1长为半径，作伸展圆弧，它的长度要足够包含俯视图上四条底边的总长度。

（4）在俯视图上，用卡规量出A1 B1长，自1点画短弧，逐次截出2、3、4、5点。

（5）连接C点和伸展圆弧上的各交截点，这些连线代表制品棱的实长。连接1-2、2-3、3-4、4-5。12345C即为正四角锥的展开图。

3.已知主、俯视图斜口直四棱锥展开图的画法

斜口直四棱锥可看成直四棱锥被正垂面截切而成，其侧面是由两个等腰梯形和两个梯形围成的，画展开图即依次画出这四个梯形的实形，如图4-74所示。

图4-74　斜口直四棱锥展开图

（a）立体图；（b）基本视图；（c）展开图

（1）按图4-74的方法作完整四棱锥展开图（底面对应边相等）。

（2）在主视图上定出斜口面与棱线相交点f′（e′）、g′（h′），引水平线与斜线s′c1和s0 c0相交，得到四个梯形面上棱线的实长（c0 f0、c0 g0……）。

（3）在四棱锥展开图上的棱线上取BF=c0 f0、CG=c0 g0……，得斜口棱线端点F、G……。

（4）顺序连接这些点，即得所求展开图。

4.放射线展开法小结

放射线展开法是很重要的一种展开方法，它运用于所有锥体及锥截管件或构件的侧面展开。尽管锥体表面各式各样，但展开方法却大同小异，作法可归纳如下：

（1）在视图中（或只在某一视图中）通过延长投影边等手段完成整个锥体的放样图。

（2）通过等分断面周长（或任意分割断面全长）的方法，作出各分点所对应的断面素线（包括棱锥侧棱以及侧面上过锥顶点的直线），将锥面分割成若干小三角形。

（3）应用求实长的方法（常用旋转法、直角三角形法），把所有不反映实长的素线，与作展开图有关的直线的实长一个不漏地求出来。

（4）以实长为准，利用交轨法（正锥体可用扇形法）作出整个锥体侧面的展开图，同时，作出全部放射线。

（5）在整个锥体侧面展开图的基础上，以放射线为骨架，以有关实长为准，再画出锥体截切部分所在曲线的展开曲线，完成全部展开图。

（三）三角形展开法

在钣金制件上，若形体的表面是由若干平面与曲面、曲面与曲面、平面与平面构成，但形体表面无平行的素线或棱线，又无集中所有素线或棱线的顶点时，不宜或不可能用平行线或放射线法直接求作展开图，则常采用三角形法展开。

1.三角形展开法的基本原理

三角形展开法是将零件的表面分成一组或很多组三角形平面或三角形曲面，求出各组三角形每边的实长，再由已求三角形边长依次拼画出各个三角形，得到展开图。必须指出，用放射线作展开图时，也是将锥体表面分成若干三角形，但这些三角形均是围绕锥顶的。用三角形法展开时，三角形的划分是根据零件的形状特征进行的，因此必须求出各素线的实长，这是准确地作好展开图的关键。

由投影原理可知，若一线段与两投影面都倾斜，则该线段在两投影面上的投影都不是其实长，求该线段实长的方法，除用前面所述的旋转法外，还可以用直角三角形法、直角梯形法和变换投影面法。这里仅介绍直角三角形法求实长（图4-75）。

图4-75（a）所示线段AB对两个投影面都倾斜，所以它的两个投影a′b′和ab都不是实长，如过B点作BC垂直于Aa，得直角三角形ABC，直角边BC=ba；另一个直角边AC就是AB两点的高度差H，恰等于AB正面投影的两个端点a′、b′在垂直方向的距离a′c′，由此可知，只要作两互相垂直的两直角边，如图4-75（b）所示，使B1C1=ab、A1C1=a′b′=H，则斜长A1B1即为线段的实长。

根据上述原理，如果已知一线段的两投影，使用直角三角形法求实长，其方法可归纳为如图4-75（c）所示，a′b′和ab为线段的两投影，求实长时，只要作一直角，在直角的一边上量取投影图ab（或a′b′）长，则另一边上量取另一视图的投影差，则直角三角形的斜边即为线段AB的实长。

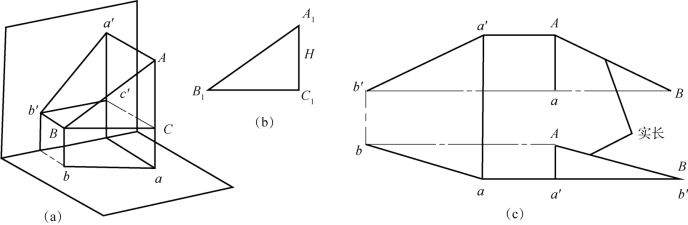
图4-75　直角三角形法求线段实长

（a）线段投影；（b）直角三角形法；（c）求线段实长方法

2.变形管接头的展开

变形管接头的展开如图4-76所示。

图4-76（a）所示的管接头，其上端管口为圆形，下端管口为正方形，用来实现方管和圆管的过渡连接（俗称“天圆地方”）。

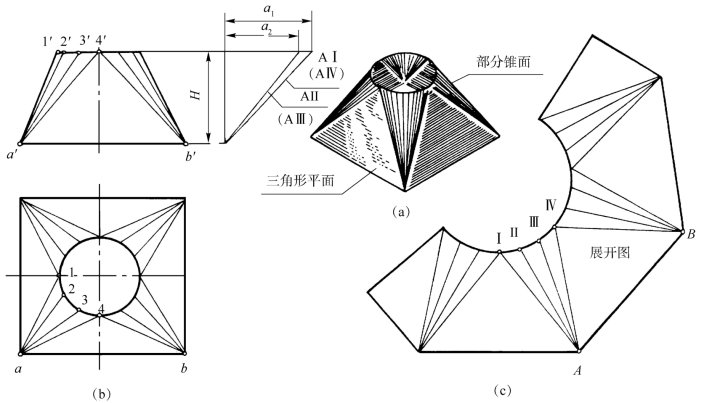
图4-76　变形管接头的展开

（a）立体图；（b）基本视图；（c）展开图

从图4-76（b）的投影分析可知，它是由四个等腰三角形平面和四个部分斜锥面围成的。

图4-76（c）是它的展开图。画展开图时，四个部分斜锥面也应分划成若干个三角形区域（图中各为三个），然后以每个三角形平面代替每一部分曲面，依次摊开与四个等腰三角形平面相连接，即得其展开图。图中锥面上各三角形的倾斜边用直角三角形法求得实长；有一个等腰三角形被对半分开布置，是为了满足接缝的工艺性要求。

3.汽车发动机罩的展开

汽车发动机罩的展开如图4-77所示。

汽车发动机罩是一块左右对称、上下两端形状不同的曲面，如图4-77（a）所示。这样的曲面只能用三角形法展开。把曲面分成若干个小三角形，求出各小三角形的实长，就能作出展开图。

图4-77　汽车发动机罩的展开

（a）基本视图；（b）直角三角形法求线段实长；（c）立体图；（d）展开图

（1）将主视图中大端的曲线分成若干份[图4-77（a）中为6份]，各份可以相等也可以不等，为了作图方便一般作等分。由于曲面左右对称，所以画一半即可。

（2）把小端的半圆曲线也分成相应份数。得1′、2′、3′……7′各点。把各对应点连成直线再对角相连，即得到许多小三角形。

（3）按投影关系在俯视图中作出各连线的投影。这样把曲线分成许多小三角形，根据主、俯两投影直角三角形法求出各线实长，如图4-77（b）所示。

（4）以7-7线为基准线（图形左右对称），向两边用实线长作出各三角形的实形即得展开图，如图4-77（d）所示。

4.三角形展开法小结

三角形展开法又称回归线展开法，因为它略去了形体原来相邻素线间的平行、相交、异面关系，而用新的三角线来代替，因此对曲面来说是一种近似的展开法。这种方法不仅可用来展开可展曲面，而且还可以作不可展曲面的近似展开图。三角形展开构件表面的三个步骤为：

（1）在放样图中将形体表面正确分割成若干小三角形。

（2）求所有小三角形的各边实长。

（3）以放样图中各小三角形的相邻位置为依据，以已知的或求出的实长为半径，通过交轨法，依次展开所有小三角形，将所得的交点视构件具体情况用曲线或用折线连接起来，由此可以得到所需构件的展开图。