干旱数据空间插值：内陆河流域风险调控技术

数据库中涉及的许多属性数据是水文气象站的观测数据，或是分布式水文模型计算单元的数据，这些数据的离散存储形式无法反映其在研究区空间上的连续分布状况，因此需要采用空间插值方法将这些离散数据“平铺”到整个研究区域。系统提供了克里金和距离平方反比两种常用的插值方法，空间插值工具界面见图8.15。

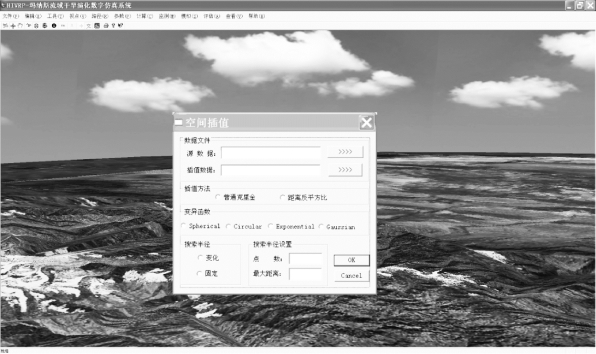
图8.15　空间插值工具界面

8.5.3.1　克里金插值法

克里金插值法建立在变异函数理论及结构分析基础上，用相关范围内的采样点来估计待插点属性值。变异函数和相关分析的结果表明，区域化变量存在空间相关性，其实质是利用区域化变量的原始数据和变异函数的结构特点，对未采样点的区域化变量的取值进行线性无偏、最优估计（见章节6.1介绍）。与其他插值方法相比，它的显著特点是使误差的方差最小。

假设区域化变量Z（x）是一个二阶平稳的随机函数，且满足本征假设，其数学期望为m，协方差函数c（h）及变异函数γ（h）存在。即：

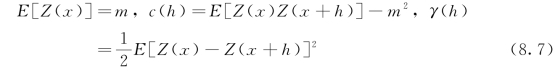
设Z（x）在n个位置取样：Z（x1），Z（x2），…，Z（xn），点x0处的估计量为：(www.xing528.com)

式中：λi为权重系数，表示空间样本点xi处的观测值Z（xi）对估计值Z*（x）的贡献量。

8.5.3.2　距离平方反比法

距离平方反比法认为待估点的值为周围已知点的加权平均值，权重大小与待估点和已知点的距离的平方成反比。距离平方反比插值的最大优点是算法简便易行，同时可以为变量值变化很大的数据提供一个合理的插值结果，当数据不存在各项异性时，其插值结果优于克里金插值。距离平方反比插值公式如下：

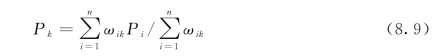
式中：Pk为待插值点的值；Pi为已知样本点值；ωik为样本点i相对于待插值点k的距离权重，取值为为样本点i与待插值点k之间的距离；n为样本点数目。

针对距离平方反比法出现的“牛眼”现象，许多学者提出了改进方法，其中具有代表性的是魏勇提出的屏蔽系数加权法［241］。该算法考虑了同一方向上距离待插值点M0较近的点Mi对于较远点Mj的屏蔽程度，引入了屏蔽系数，在方位-距离加权法的基础上，利用吸引子分维数、Hurst指数在变化复杂程度高者取小权、低者取大权的指导思想，进一步改进了方位-距离加权法。即认为Mi、Mj对M0的值都有影响，但Mj对M0的影响受到Mi的屏蔽，且屏蔽效应应简单化、绝对化，大部分情况下是不完全屏蔽。本书采用此算法提高距离平方反比法的插值精度，具体步骤请参看相关文献。