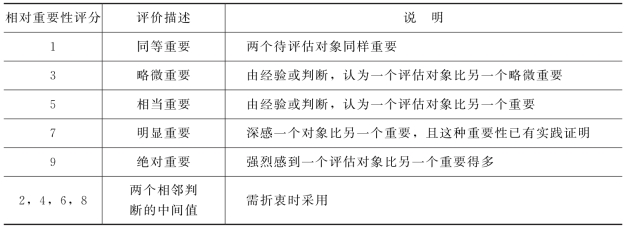
（1）确定待评估对象重要性判断矩阵A。判断矩阵A的确定如章节4.3.1，为便于确定aij值，美国运筹学家、匹兹堡大学教授托马斯·塞蒂（T.L Saaty）在提出层次分析法时，建议采用1～9标度的重要性判断矩阵，并给出了待评估对象间相对重要性等级表（见表4.8）。
表4.8 待评估对象重要性判断矩阵A中元素的取值
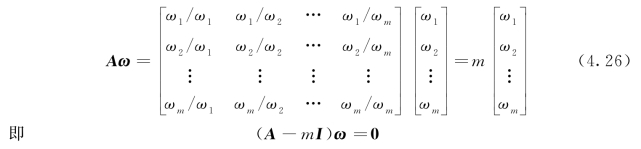
（2）推求权向量。
式中：I为单位矩阵，如果A估计不够准确，则A中元素的微小扰动就意味着特征值的微小变化，从而有：
式中：λmax为矩阵A的最大特征值。
由式（4.27）可以求得特征向量即权向量ω=［ω1，ω2，…，ωm］T。
用特征向量法可求最大特征值λmax，但求解时需要解m次方程，当m≥3时计算较麻烦。这时可采用近似算法（LLSM法），该方法的主要步骤如下：
（1）A中每行元素连乘并开m次方：
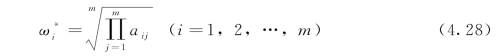(www.xing528.com)
（2）求元素的权重：
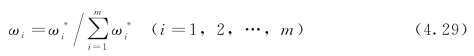
（3）A中每列元素求和：
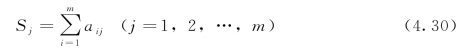
（4）求λmax值：
（5）一致性检验。
用λmax～m度量矩阵A中各元素aij（i，j=1，2，…，m）估计值的一致性。单个判断矩阵的一致性检验分为以下步骤：首先，计算矩阵的最大特征值λmax，并计算一致性指标（CI）；其次，按照矩阵阶数在随机一致性指标均值表（见表4.9）中查询相应的随机一致性指标均值（RI）；再次，按照下式计算出CR值：
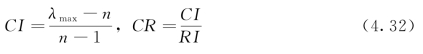
若CR＜0.1，则可认为A中aij的估计基本一致，一致性检验通过，否则需调整矩阵A中元素aij的值，再重新按照检验步骤进行检验，直至CR＜0.1。
表4.9 m阶矩阵的随机指标均值
特征向量法是将判断矩阵的最大特征根所对应的归一化特征向量作为排序权值，不足之处是权值计算与判断矩阵的一致性检验是分开进行的，当判断矩阵一致性程度很差时，求解特征值较困难。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
