街道网络中心性指标及应用领域

在社会学之外，中心性研究被迁移到其他网络研究中，包括城市街道网络。对于城市空间而言，中心性“以可度量的距离保留了空间要素的地理属性”[5]，可以被看做一种基于可达性的重要程度量化指标。

在既往的研究文献中，大约有十几种不同的街道网络中心性指标被定义，大致可分为以下几类：使用接邻属性衡量的；使用中介属性衡量的；使用系统相对属性衡量的；基于空间句法理论的。前三类大多使用原图，第四种使用对偶图。借助中心性的分布特征可以对城市空间结构进行研究，而不同种类的中心性又有各自擅长的领域（表2—1）[6]。

表2—1 部分中心性指标一览表

续表

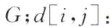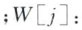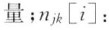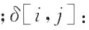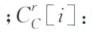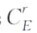
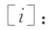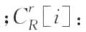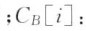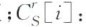注1：G：网络图点i和j之间的距离；r：搜索半径点j的权重；njk：点j和点k之间最短路径的数：点j和点k之间的最短路径经过点i的数量点i和点j之间的平面直线距离接近性值偏心性值：可达范围中间性值直线性值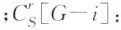：删除与点i联系的边后图G 的直线性值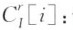；信息中心性。

注2：此公式是按照“边来定义的”。其中，Rx：在链接x的搜索半径内所有网络连线的集合；P（y）：搜索半径内任意连线y的比例；W（y）：连线y的权重；d M（x，y）：在网络中按照某种度量测得的起始连线x与终点连线y之间距离

注3：中心性的数学表达式和定义细节在不同文献中略有差别，本表中NQPD出自Cooper C.Spatial Design Net-work Analysis（s DNA）version3.3Manual.Cardiff University，2016.Available，http://www.cardiff.ac.uk/sdna/soft-ware/documentation.4.4，其余的除偏心性和信息中心性外都出自Sevtsuk Andres，Michael Mekonnen.Urban Network Analysis：A Toolbox for Arc Gis10.UNA 帮助文件.2013

在介绍不同类型的中心性指标前，还需要简单介绍一下搜索半径和权重的概念。搜索半径r[7]是指纳入中心性计算的任意两个点[8]之间的最远距离（图2—2），通过设定搜索半径可以将所有距离点i在r以内的j纳入计算，而把r以外的点排除。权重W[i]是附载于空间点之上的人口、面积、地价等参数，可以用来表征社会经济情况。这两个参数在中心性分析的应用中还具有更为深刻的意义，将在后文介绍。

图2—2 搜索半径r和可达范围指标示意

1）使用接邻属性衡量的中心性

如果一个点到达其他点的距离越近或者与某个点接邻的其他点的数量越多，则可以说这个点越中心，是最常见的中心性指标类型。典型指标包括：接近性（Closeness）、远离性（Remoteness）、平均测地距离（Mean Geodesic Length）、联系度（Network Quantity Penalized by Dis-tance，NQPD）、偏心性（Eccentricity）、可达范围（Reach）、度（Degree）等。有学者认为，空间句法中的重要指标整合度（Integration）本质上也是一种接近性指标[9][10]。

（资料来源：Sevt-suk A. Path and Place:A Study of Urban Geometry and Retail Activity in Cambridge and Somerville, MA [D].PhD disserta-tion in Urban De-sign and Planning, Massachusetts In-stitute of Technol-ogy,2010:84)

①接近性、远离性

接近性表示在总体上某点距离其他点的远近程度，通常使用某点i到图G 中其他所有点j距离总和的倒数来表示。远离性与接近性本质上一致，是接近性的相反表达。

②偏心性

用来衡量网络中某点与其最远点之间联系的方便程度，通常使用一定搜索半径r内点i距其最远点j距离的倒数来表示。

③可达范围和度

用来度量搜索半径范围r内，从某点i出发可到达其他的点j的数量。如果把r设定为按节点计算的拓扑距离1（由i点出发只经过1个节点），则此时的可达范围也可称为度（Degree）

④联系度

联系度[11]（NQPD）是由Cooper等提出的，它“同时将网络中权重的量值和其可达性纳入考量，而远离性（Farness）仅仅考虑了可达性”[12]。因此，这一指标实际上综合了可达范围和接近性，在后文的部分案例分析中将使用该指标。当不考虑上述两方面各自的重要程度差别时，它就是某点搜索半径内所达权重与距离的比值之和，数学表达式见表2—1。与之近似的是Sevtsuk等人使用的引力值（Gravity）指标，与NQPD的差别在于对按距离衰减现象的衡量方式不同。

以上由接邻属性衡量的中心性指标可以用来解决城市中的各种选址问题。基于目标功能的选址问题基本可分为三类[13]：第一，使用最大距离的最小化准则（Minimax Criterion），即根据最不利的目的地来确定选址，如医院。第二，使用总量最小化准则（Minisum Criterion），即根据到所有目的地距离的总和来选址，如绿地、社区中心等。第三，适用于竞争性环境的选址问题，如商业设施，通过地点能够服务的市场份额来确定选址。偏心性、接近性和可达范围三个指标可以分别对应于上述三类选址问题，而NQPD则综合了后两种指标。一些学者已经在理论层面阐述了利用它们来进行选址分析的可行性[14]，实证研究的案例主要集中在商业服务设施方面[15][16][17]。

2）使用中介属性衡量的中心性

上面的一类指标所关注的是起点与目标点之间的关系，而此类中心性关注第三点作为另外两点联系中介的属性。一般认为，两个点之间的联系总是沿着最短的路径，因此，最短路径也可以看做是两点间“联系流”（Flow）的一种“代理”（Proxy）[18]，由此产生了中间性（Betweenness）等指标。

中间性指标通过图中j、k两点间最短路径经过某点i的数量来表征其在网络中的关键性程度。当两点间的最短路径不止一条时，就计算经过i的最短路径占j、k间所有最短路径数量的比值[19]。其基本定义为：图G中搜索半径r内经过点i的任意其他两点j、k间的最短路径的数量与j、k之间所有最短路径数量的比值之和。

中间性是街道网络中心性研究中出现最为频繁的指标。它的“空间分布给出了空间与道路网络之间相耦合的重要信息”[20]，也就是说它能模拟街道中“联系流”的强弱，可以被用作交通研究[21]。此外，也可用来进行基于交通流的空间要素分布研究，如商业地块、公交、轨道交通站点、零售店铺的分布[22][23]等。

3）使用系统相对属性衡量的中心性

此类指标通过要素在两种不同网络中的对比来衡量其中心地位。

①直线性和分散率

直线性表征的是按网络联系与按直线联系之间的相对差距，即在何种程度上从i点至其他所有点的最短路径符合几何直线路径，定义为：图G中搜索半径r范围内某点i到所有其他点j的直线距离和最近的网络距离的比值之和。直线性主要被用来进行城市结构的理论研究。类似的指标还有分散率，其差别在于进行累加的是网络距离与直线距离的比值。

②信息中心性(www.xing528.com)

网络是一个系统，某一个要素的变动或缺失都将引起整个系统属性的改变，因此，“在没有某边或点的情况下，图G的某种品质的损失可以看做其在网络中的‘中心’程度”[24]。即通过一个点被取消后的网络与原网络的属性对比来衡量其中心性。如“信息中心性”（Information）通过网络整体直线性的变化比率来定义该点中心性。在理论上，此类中心性能够对道路体系调整或规划的决策起到支撑作用，但目前尚未发现相关的研究文献，其主要应用于城市空间结构的理论研究。

4）基于空间句法的中心性

一些研究者证明，虽然有自身独特的理论体系，空间句法本质上也是一种中心性方法，其核心指标整合度（Integration）可以看做是一种经过标准化的接近性指标[25]。近年来，空间句法在我国学界和工程实践中应用广泛，对其理论方法、主要指标和计算工具的介绍资料众多，本书不再赘述。

[1]Brandes U,Erlebach T[Eds..Network Analysis[M].Berlin:Springer-Verlag Berlin Limited, 2005:19

[2] Bavelas A. A mathematical model for group structures[J]. Human Organization 1948(7): 16-30

[3]② Freeman L. A set of measures of centrality based on betweenness[J]. Sociometry,1977(40):35-41

[4]③ Freeman L. Centrality in social networks:conceptual clarification[J]. Social Networks,1979(1):215-239

[5] Secllato S,Cardillo A , Latora V,etc. The backbone of a city[J]. The European Physical Journal B, 50(1-2),2006: 221-225

[6] 本节中所介绍的主要中心性指标的定义、公式等出处文献均在表2—1中注明，文中不再标注。

[7] 搜索半径使用网路距离而非直线距离度量，在不同文献中的其具体名称略有不同，意义一致。

[8] 中心性的计算既可以对点也可以对边，为行文方便，除特别说明之处外，本节中都用点来定义。

[9]①Crucitti P,Latora V,Porta S.Centrality in network of urban streets[J].Chaos An Interdiscipli-nary Journal of Nonlinear Science,2006,16(1):015113

[10]② Sevtsuk A. Path and Place: A Study of Urban Geometry and Retail Activity in Cambridge and Somerville, MA[D] . PhD dissertation in urban design and planning, Massachusetts Institute of Technology,2010. 45

[11] 按照英文直译，该指标应译为“按距离衰减的网络值”，为表述方便，作者根据内涵意义将其命名为联系度。

[12]Cooper C.Spatial Design Network Analysis(sDNA)version 3.3 Manual.Cardiff University, 2016Available,http://www.cardiff.ac.uk/sdna/software/documentation.4.4

[13]Louis Hakimi.Optimum location of switching centers and the absolute centers and medians of a graph[J].Operations Research,1964(12):450-459

[14]4④Brandes U,Erlebach T[Eds.].Network Analysis[M].Berlin:Springer-Verlag Berlin Limited,2005

[15]⑤Sevtsuk A.Path and Place:A Study of Urban Geometry and Retail Activity in Cambridge and Somerville,MA[D].PhD dissertation in Urban Design and Planning,Massachusetts Institute of Technolo-gy,2010

[16]⑥Wang Fahui,Chen Chen,Xiu Chunliang,etc.Location analysis of retailstore in Changchun,Chi-na:A Street Centrality Perspective[J].Cities,2014(41):54-63

[17]⑦Porta S,Latora V,Wang F,ect.Street centrality and densities of retail and services in Bologna, Italy[J].Environment&Planning B:Planning&Design,2009,36(3):450-465

[18] Marc Barthelemy. Spatial networks[J]. Physics Reports,2011(499):20

[19]各种不同的中间性定义中，对这种情况的处理方式略有不同，具体可参考陈晓东.基于中间性（Be-tweenness）的城市街道网络研究综述[C]//：规划60年：成就与挑战——2016中国城市规划年会论文集.北京：中国建筑工业出版社，2016

[20] Marc Barthelemy. Spatial networks[J]. Physics Reports,2011(499):20

[21] Lammer S,Gehlsen B, Helbing D. Scaling law in the spatial structure of urban road networks[ . Physica A ,2006(363):89-95

[22]⑤ Zhang Lingzhu,Chiaradia A , Zhang Yu.A Configrational Accessibility Studyof Road and Metro net-work in Shanghai,China,in Q Pan,J Cao[Eds.]. Recent Developments in Chinese Urban Planning[M .Switz-erland:Springer International Publishing,2015

[23]⑥ Sevtsuk A. Networks of the built environment,in D.Ofenhuber& C. Ratti,eds. [De]codingthe Tity-How Big Data Can Change Urbanism. Birkhäuser,2013.144-159

[24]Brandes U,Erlebach T[Eds.].Network Analysis[M].Berlin:Springer-Verlag Berlin Limited,2005. 36

[25]Crucitti P,Latora V,Porta S.Centrality in network of urban streets[J].Chaos An Interdiscipli-nary Journal of Nonlinear Science,2006,16(1）:015113