加权平均值VS几何平均值

在科学实验中，虽然实验误差在所难免，但平均值可综合反映实验值在一定条件下的一般水平，所以在科学实验中，经常将多次实验值的平均值作为真值的近似值。平均值的种类很多，在处理实验结果时常用的平均值有以下几种。

（一）算术平均值

算术平均值是最常用的一种平均值。设有n个实验值：x1，x2，…，xn，则它们的算术平均值为

式中　xi——单个实验值，下同。

同样实验条件下，如果多次实验值服从正态分布，那么算术平均值是这组等精度实验值中的最佳值或最可信赖值。

（二）加权平均值

如果某组实验值是用不同的方法获得的，或由不同的实验人员得到的，那么这组数据中不同值的精度或可靠性是不一致的，为了突出可靠性高的数值，则可采用加权平均值。设有n个实验值：x1，x2，…，xn，则它们的加权平均值为

式中　w1，w2，…，wn——单个实验值对应的权重。

如果某值精度较高，那么可给以较大的权重，加重它在平均值中的分量。例如，如果我们认为某一个数比另一个数可靠两倍，那么两者的权重的比是2∶1或1∶0.5。显然，加权平均值的可靠性在很大程度上取决于科研人员的经验。

实验值的权重是相对值，因此可以是整数，也可以是分数或小数。权重不是任意给定的，除了依据实验者的经验之外，还可以按如下方法给予：

（1）当实验次数很多时，可以将权重理解为实验值xi在很大的测量总数中出现的频率n i/n。

（2）如果实验值是在同样的实验条件下获得的，但来源于不同的组，这时加权平均值计算式中xi代表各组的平均值，而wi代表每组实验次数，见例1-1。若认为各组实验值的可靠程度与其出现的次数成正比，则加权平均值即为总算术平均值。

（3）根据权重与绝对误差的平方成反比来确定权重，见例1-2。

【例1-1】在实验室称量某样品时，不同的人得4组称量结果如表1-1所示，如果认为各测量结果的可靠程度仅与测量次数成正比，试求其加权平均值。

表1-1　例1-1数据表

解：由于各测量结果的可靠程度仅与测量次数成正比，所以每组实验平均值的权值即为对应的实验次数，即w1=3，w2=2，w3=5，w4=3，所以加权平均值为(www.xing528.com)

【例1-2】在测定溶液pH值时，得到两组实验数据，其平均值为：1=8.5±0.1；2=8.53±0.02，试求它们的平均值。

解：

（三）对数平均值

如果实验数据的分布曲线具有对数特性，那么宜使用对数平均值。设有两个数值x1，x2都为正数，则它们的对数平均值为

注意：两数的对数平均值总小于或等于它们的算术平均值。如果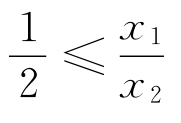＜2时，可用算术平均值代替对数平均值，而且误差不大（不大于4.4%）。

（四）几何平均值

设有n个正实验值：x1，x2，…，xn，则它们的几何平均值为

等式两边同时取对数，得

可见，当一组实验值取对数后所得数据的分布曲线更加对称时，宜采用几何平均值。一组实验值的几何平均值常小于它们的算术平均值。

（五）调和平均值

设有n个正实验值x1，x2，…，xn，则它们的调和平均值为

或

可见调和平均值是实验值倒数的算术平均值的倒数，它常用在涉及与一些量的倒数有关的场合。调和平均值一般小于对应的几何平均值和算术平均值。

综上所述，不同的平均值都有各自适用场合，选择哪种求平均值的方法取决于实验数据本身的特点，如分布类型、可靠性程度等。