风积沙工程试验结果与分析

1）HDPE条带及焊缝拉伸试验

土工格室加固沙与其他加固土（如结合料加固土）有根本区别，土工格室以土中加筋的方式实现加固土体的目的，而并未改变土颗粒间的接触条件。因此土工格室加固沙的强度和稳定性直接依赖土工格室的支持，这决定了土工格室自身的强度和抗变形能力具有重要意义。鉴此对HDPE条带及其焊缝进行了拉伸试验。

（1）HDPE条带拉伸试验。

条带拉伸试验的试验曲线彼此相似，如图7-9所示为其中之一，表7-3列出了试验结果。

图7-9　HDPE条带拉伸应力-应变曲线

①HDPE条带具有较好的线弹性性质。图7-9直观地反映了条带拉伸过程中应力和应变之间的关系，试验曲线十分接近直线。从表7-3应力应变线性相关系数一栏中还可以看出，线性相关系数接近1，且变化不大，说明这一关系是显著且稳定的。

②HDPE条带具有较高的强度和较大的韧性。表7-3所列的极限强度和相应的延伸率已远大于土工格室在路面结构中格室壁实际的工作应力应变，而材料实际的强度和断裂延伸率远大于表列数值。表列强度是试验极限荷载除以试件横截面面积所得，而试验中试件在达到极限荷载相应的延伸率时已有了明显的“颈缩”，因此材料的实际强度要比表列数值大。可见，在路面结构正常使用时，土工格室不会因材料抗拉强度不足或变形能力不足而产生破坏。

③HDPE条带具有较高的拉伸模量。路面结构层在正常工作状态下，不可能产生大的变形，要发挥土工格室材料的强度优势，相对较高的模量是必不可少的条件。

（2）HDPE条带焊缝拉伸试验。

焊缝拉伸试验结果见表7-4。从表中所列焊缝强度可以看出，试验所用的土工格室具有较高的焊缝强度，其平均值略大于《土工格栅产品说明书》给出的100N／cm的焊缝强度指标。与实测的土工格室壁工作应力相比，焊缝已具备足够的抗剥离强度。

2）HDPE条带蠕变试验

蠕变是多数高分子合成材料具有的特性之一。土工格室加固沙中，作为加筋的土工格室，若产生蠕变断裂或蠕变破坏，同样将导致加固土的破坏。因此有必要对格室材料的蠕变特性进行研究，考察其持荷后变形的发展规律。

表7-3　HDPE条带拉伸试验结果统计

表7-4　HDPE条带焊缝强度计算表

该试验进行了不同应力下的蠕变试验，共获得36条试验曲线，其中5条含卸载过程，如图7-10a所示，其余31条曲线如图7-10b所示。为便于比较，图7-11给出了不同应力量级的8条曲线，图7-12为对应于图7-11的应变率曲线，即应变对时间的差商。从试验结果可以看出：

图7-10　HDPE条带蠕变试验曲线

图7-11　不同应力下的蠕变试验曲线

图7-12　不同应力下蠕变试验的蠕变应变率曲线

①HDPE条带的应变-时间曲线具有典型蠕变曲线的形式，具备较明显的“过渡蠕变阶段”和近似的“稳态蠕变阶段”，说明HDPE材料具有较大的黏性。当土工格室加固土结构层需长期持荷或反复加载且变形难以及时恢复时，应重视格室带来的时间效应。

②不同应力下的蠕变试验曲线，及其相应的蠕变应变率曲线，其形状基本相似。虽然随着应力量级的提高，初始应变增大，过渡蠕变阶段延长，蠕变应变增大，但就蠕变应变的发展趋势来看，各试验曲线反映了一致的规律性。蠕变应变经初始阶段的快速增长后，应变速率很快衰减到0～2με／min的低水平，并且仍保持缓慢衰减的趋势。

③材料的蠕变强度可以有多种定义，极端的情形是蠕变断裂强度，即在运营期间，材料不因长期持荷而发生断裂的最大应力。由于HDPE等高分子合成材料往往具有很大的断裂延伸率，因而工程实际可能更关注这样的蠕变极限：一是在规定的加载时间内，使材料产生规定应变速率的应力；二是在规定的加载时间内，使材料产生规定蠕变应变的应力。基于这两种定义，根据试验结果可以推断，HDPE条带的蠕变强度应不低于5.3MPa。对比模型应力应变试验结果，从图7-13的荷载-应力曲线中可以看出，HDPE条带亦具有足够的蠕变强度。

图7-13　1＃荷位荷载应力、应变曲线

3）土工格室沙结构层应力应变试验

土工格室加固沙方法属机械加固法，在不改变加固对象内部结构的情况下，使沙获得高的强度，则加固材料必定要承受比加固对象大的应力，或者改善加固对象受力后的工作状态，或两者兼有。因此土工格室在加固沙中的作用亦应不外乎两个方面：一是利用HDPE条带高的抗拉强度，以承受较大拉应力的方式来分担部分荷载；二是格室的受力单元张紧后，格室壁的紧箍作用限制了填料的侧向位移，阻止其剪切滑动或破坏，而充分发挥沙（或砂砾等松散颗粒状填料）抗压强度高的优势。然而土工格室在加固沙中实际的受力状态还需经试验才能有所了解，由此分析土工格室在加固沙中是否发挥作用。

为使荷位明确，将荷载限制在一个格室单元之中，以区分受荷和不受荷格室单元。由于格室单元的实际形状并非正方形，而类似菱形，且是曲边的，故30cm直径的承载板不能完全放入一个格室中，所以试验采用了18cm直径的承载板，荷载完全处于一个格室单元中，其周边格室均不受荷。

该试验对三个荷位均进行了重复试验，1＃荷位共进行了4次试验，2＃和3＃荷位各进行2次试验。试验具有较好的再现性，试验曲线保持了稳定的规律性，试验结果是可信的。

纵观各试验曲线，不难发现：

①在荷载作用下，土工格室中产生了较大的应力和应变。图7-13～图7-15给出了三个荷位第一次测试的荷载-应力、应变曲线。虽然由于测点与荷位的相对位置不同，测得各格室壁的应力、应变差别较大，受力情况有拉有压，但从各曲线可以看出，凡受力较大的格室壁，如图7-13中的1、2、5、6、9、10、13、14各测点，图7-14中的1、2、3、4、13、14、15、16各测点，图7-15中的5、6、7、8、13、14、15、16各测点，其应力应变与荷载几乎成比例地快速增长。当荷载达到0.7MPa时，各测点的应变值见表7-5，最大拉应变达1852.5με，即产生2.634MPa的拉应力；最大压应变达777.5με，即产生1.105MPa的压应力。土工格室壁中应力、应变对荷载的这种敏感性，说明了土工格室在加固沙中起着十分重要的作用。

图7-14　2＃荷位荷载应力、应变曲线

表7-5　各点应变（×10-6）（荷载：0.7MPa）

（续表）

图7-15　3＃荷位荷载应力、应变曲线

②土工格室对填料存在明显的侧向限制作用。作为土工格室加固土这种复合土工材料的一个组成部分，承受荷载是土工格室的基本作用，但是土工格室作为一种加固手段，更值得关注的是其加固作用是否存在。这里的加固作用并不加强填料的粒间强度，而是改善填料受力后的工作条件，即给填料提供侧向限制以提高其承受荷载的能力。因此仍需从应力、应变角度来分析。

表7-6列出了0.7MPa荷载下各测点处格室壁中应变测试结果的平均值。表列数据表明，并非所有的格室壁均受拉，有的格室四壁受拉，有的四壁受压，有的则有拉有压，受力情况较为复杂。为便于分析，图7-16以1＃荷位为中心对格室壁进行了编号，图7-17～图7-19将0.7MPa荷载下的应变测试结果按测点位置标绘于格室简图上，并且对2＃和3＃荷位进行了平移，使其与1＃荷位对齐。这样可将图7-17～图7-19叠置，便可获得荷位附近各格室壁的应变分布情况，如图7-20所示。

表7-6　测点处各边（格室壁）的应变（×10-6）

注：荷载为0.7MPa。

图7-16　格室壁编号

图7-17　1＃荷位0.7MPa荷载下测点处格室壁应变（×10-6）

图7-18　2＃荷位0.7MPa荷载下测点处格室壁应变（×10-6）

图7-19　3＃荷位0.7MPa荷载下测点处格室壁应变（×10-6）

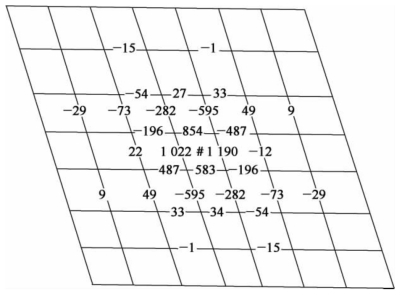
图7-20　0.7MPa荷载下荷位附近格室壁的应变（×10-6）

注：图中“＃”号表示荷位所在格室单元

如图7-17所示，荷载所在格室单元的四壁产生了较大的拉应变，说明它们受到较大拉应力的作用。但是土工格室并未受到荷载的直接作用，产生这一试验现象的唯一原因是格室单元中的填料受到竖向荷载的作用产生侧向压力，同时产生侧向位移，挤压格室壁而使其张紧、拉伸。这说明填料对格室壁有明显的压力，也说明了格室壁对填料有明显的压力。这便是土工格室侧向限制作用的基本形式。这种类似环向应力的“紧箍”作用，能有效阻止填料发生剪切破坏。表7-7给出了格室壁两侧侧向压力之比，从表中2／1、6／5、10／9及14／13各行可以看到，格室壁外侧（非受荷格室单元一侧）和内侧（受荷格室单元一侧）的侧压之比，在0.456～0.857，即外侧侧压力比内侧侧压力减小14.3%～54.4%。由于格室壁两侧压力盒是背靠格室壁对称埋置的，如图7-21所示。从理论上说，格室壁如无侧限作用，两压力盒测得的侧压力应严格相等，即使考虑试验误差，两压力盒的测试结果也应基本相等。因此表7-7反映的试验现象，即填料中侧压力在格室壁处变化不连续，产生跳跃式减小，正说明了受荷格室单元四壁发挥了显著的侧向限制作用。

图7-21　压力盒埋置示意图

表7-7　格室壁两侧侧压力之差

（续表）

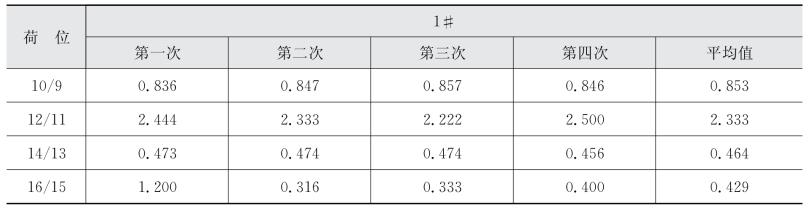
注：荷载强度为0.7MPa。

③土工格室的侧向限制作用对填料中的竖向应力有显著影响。从试验结果看，土工格室不仅对水平方向的应力传递有很大的限制作用，对填料中竖向应力的传递也有明显影响。就荷载-压力试验曲线做一般性比较就可以看出，1＃荷位与2＃、3＃荷位的测试结果有根本的区别，做进一步的比较还发现，1＃荷位中，测点位于受荷格室单元内的各点，测得的竖向压力远大于其余各测点的测试结果（图7-22），而受荷格室单元以外的各测点，包括2＃及3＃荷位的测试结果，相差很小，且压力值也很小。这说明竖向压力的衰减主要是在受荷格室的格室壁处完成的，表7-8给出了1＃荷位0.7MPa荷载下格室壁两侧竖向压力的比值。表中2／1、6／5、10／9及14／13各行反映了受荷格室单元格室壁内外两侧竖向压力的变化，外侧竖向压力与内侧之比在0.004～0.074，即从格室壁的内侧到外侧，竖向压力减小了92.6%～99.6%。由于内外两侧压力盒是紧靠格室壁埋设的，因此竖向压力的急剧变化绝非测点相对荷位的距离变化所致，而只能是格室壁的存在“阻断”了竖向压力的传递，使得荷位以外的格室中，竖向压力均很小。也就是说，土工格室作为一种侧限系统，不仅对水平方向的侧压力有效，对竖向的正压力亦有效，因此土工格室的侧向限制作用是对荷载的有效禁锢，能可靠地防止填料产生如图7-15a所示的破坏，使加固沙获得较高的强度。(www.xing528.com)

图7-22　1＃荷位第一次测试荷载-竖向压力曲线

表7-8　竖向压力之比（荷载：0.7MPa）

至于荷位邻近格室单元，2＃及3＃荷位的试验对其进行了测试。从图7-18和图7-19可以看出，格室壁以受压为主。

图7-16中编号为5、6、7、8的格室壁和编号为11、12、5、6的格室壁，它们与受荷格室直接相连，产生了较大的压应变。图7-19中编号为5、6、7、8、9、10、11、12的格室壁均受到较大的压应力，因而产生了较大的压应变。反过来说，是土工格室壁中有较大的、指向荷位的应力。显然，这和编号为1、2、3、4的格室壁的侧向限制作用是协调一致的，只是方式不同。编号为1、2、3、4的格室壁以受拉方式发挥作用，形成“环向紧箍”，编号为5、6、7、8、9、10、11、12的格室壁则以受压方式发挥作用，形成“径向支撑”。如果进一步扩大分析范围，如图7-20所示，有这样的趋势：编号为13～24的格室壁又构成一个“环向紧箍”，类似于一个大格室单元。由此可以推测土工格室侧向限制作用的一种模式：环向受拉发挥“紧箍”作用；径向受压发挥“支撑”作用。由于编号12以后的格室壁受力较小，变形也小，其初始状态往往影响其应变测量结果的正负号，故编号12以后的格室壁的作用有待扩大测试范围，做进一步试验研究。

4）路面结构模型蠕变试验

路面结构模型的蠕变试验从两个方面测试了不同荷载强度下模型的响应：一方面是土工格室沙结构层表面竖向位移与时间的关系；另一方面是土工格室沙结构层中测点处格室壁的应变与时间的关系。

由路面结构模型的应力-应变试验可知，引起测点处格室壁产生较大应力的是1＃荷位的荷载。可以推断，在1＃荷位持荷同样可能引起各测点处格室壁产生应变的增长。1＃荷位的蠕变试验进行了两组，第一组荷载强度从0.05MPa开始，第二级为0.1MPa，以后每级按0.1MPa增至0.7MPa，加载图如图7-23所示。图7-24给出了土工格室沙结构层表面竖向位移曲线，图7-25给出了各测点应变曲线。第二组试验荷载强度为0.6MPa、0.7MPa、0.8MPa，如图7-26所示。图7-27给出了土工格室沙结构层表面竖向位移曲线，图7-28为各测点应变曲线。比较两组试验相应的曲线可以看出，两组试验相互吻合，曲线形状及测点间应变的相对关系保持一致。因此试验结果在定性分析中是可以充分接受的。

图7-23　第一组试验加载

图7-24　第一组试验竖向位移-时间曲线

图7-25　第一组试验各测点应变-时间曲线

图7-26　第二组试验加载图

图7-27　第二组试验竖向位移曲线

从图7-24与图7-25、图7-27与图7-28可以看出，结构层表面竖向位移与结构层内格室壁的应变具有基本一致的变化规律，在蠕变速率的变化率上，竖向位移曲线显得略大。由两者之间的这种关系以及“在同一级荷载（P）的作用下，风积沙的沉降很快完成（＜15s），基本不产生徐变”可以推断，土工格室沙结构层表面竖向的蠕变主要是由格室壁的蠕变引起。而这一点从蠕变的角度又说明了土工格室在土工格室加固沙中的作用和土工格室侧向限制的重要性。因为若无土工格室的侧向限制，填料将产生剪切破坏，结构层表面竖向位移不再是趋于稳定的蠕变，而是丧失稳定性的破坏变形。当然，要引起填料的破坏，必须有足够大的荷载，也就是说不可能在荷载很小的情况下充分发挥土工格室的侧向限制作用，亦即在荷载很小时，土工格室不可能充分表现其黏性。这样，在对模型的测试结果中，必定要包含一些对时间呈线性变化的曲线。图7-24～图7-26恰好证实了这一分析，当荷载小于0.6MPa时，各级荷载下的竖向位移-时间曲线均呈线性，且变形速率极小，即属于“沉降很快完成”“基本不产生徐变”的情形。当荷载P≥0.6MPa时，竖向位移-时间曲线呈现出非线性，且具备了“过渡蠕变”的曲线雏形，尤其是在图7-27中，P=0.8MPa时，曲线已基本上具备了典型蠕变曲线的形状。图7-25～图7-28也具有类似的特性，所不同的只是由于测点间的差异，这种荷载的分界点没有统一的数值，而是各测点有各自的荷载分界点。虽然以上的分析是针对梯级加载试验曲线进行的，但由于线性曲线叠加后仍保持线性，故一次性加载的蠕变曲线应具有相似的性质。

图7-28　第二组试验各测点应变时间曲线

至于竖向位移-时间曲线蠕变速率的变化率略大于应变-时间曲线，是由于竖向位移除了因格室单元侧向扩张引起以外，还有风积沙的压缩和结构层整体的变形，而至少风积沙的压缩变形是很快完成的。因此竖向位移具有较大蠕变速率的变化率是必然的。

此外，比较该试验的应变-时间曲线和土工格室材料条带的蠕变曲线，不难发现，当初始应变相等或相近时，条带蠕变具有更大的蠕变速率和蠕变速率的变化率。即在相同应力作用下，作为单轴位伸的HDPE条带，较之埋置在填料中的格室壁将产生更大的蠕变变形。说明在土工格室加固沙结构层中，HDPE条带具有更高的抵抗蠕变变形的能力。

通过对试验结果的分析可以得到：

①土工格室单元的蠕变扩张对结构表面竖向蠕变变形有重要影响，荷载越大，土工格室侧向限制越明显，这种影响也越大，竖向位移-时间曲线随荷载的增大，从线性向典型蠕变曲线形状发展。

②土工格室使得土工格室加固沙具有与纯沙极不相同的流变特性。在受到竖向荷载作用时，纯沙的沉降-时间曲线为折线，沉降完成快，几乎不产生蠕变，如图7-29所示，而土工格室沙显然具有非线性的竖向位移-时间曲线。

③以HDPE条带单轴拉伸蠕变试验的结果描述加固土中格室壁的蠕变形态是偏于安全的。

5）土工格室沙结构层宏观抗压回弹模量测试

抗压回弹模量是路面材料重要的力学指标之一，是现行路面结构设计计算方法中不可或缺的基本参数。要使土工格室沙结构层设计摆脱盲目、纯经验的状态，纳入现行路面结构设计计算体系之中，必须获得土工格室沙结构层抗压回弹模量这一最基本的参数。这至少可以使土工格室沙结构层设计达到“厚度计算”这一水平。当然要完全按现行路面结构设计计算方法来设计土工格室沙结构层，尚需要进行更深入的研究，获得更多的设计参数。

图7-29　风积沙的沉降曲线

（1）室内模型试验。

室内试验对模型的沙基、砂砾及不同规格的土工格室沙结构层进行了测试。试验结果见表7-9～表7-11。土工格室规格以“格室边长（cm）×格室深度（cm）”表示。表中代表值计算时，参照《公路工程质量检验评定标准》（JTJ071—1994），保证率取95%。

表7-9　沙基砂砾模量统计表　（MPa）

表7-10　土工格室沙模量统计表（一）　（MPa）

注：按二层体系反算土工格室沙结构层模量。

表7-11　土工格室沙模量统计表（二）　（MPa）

注：按三层体系反算土工格室沙结构层模量。

表7-12　p-l曲线线性相关系数统计表

（2）测试结果分析。

①无论测试层位是沙基顶面、土工格室沙顶面，还是砂砾结构层顶面，修正后的p（荷载）l（回弹变形）曲线具有良好的线性性质，尤其是室内模型试验，p-l曲线的形状也十分相似。从图7-30中可以看出，曲线的起始端出现反弯，即随着荷载的增大，也在增大，根据试验方法的规定，这应予以修正。显然修正以后的曲线与线性回归所得的直线几乎重合，可见测试结果波动很小，相当稳定。表7-12列出了试验结果线性相关系数的统计情况，说明p与l之间存在显著的线性相关关系，也就是说，就竖向荷载和回弹变形而言，由沙基、土工格室沙及砂砾组成的路面结构是一个线性体系，这对引用现行路面结构设计计算方法是很重要的。

②在试验覆盖范围内，土工格室规格的变化对土工格室加固沙的抗压回弹模量没有显著影响。

图7-31反映了模量（平均值）与格室深度的关系。深度为10cm时，三层体系反算的模量显著大于其余两点的模量。考虑结构层相对较薄，反算结果易于偏高，且分层测定模量时，一般应使层厚在20～30cm，为安全应谨慎处理该点数据，仅供参考。

图7-30　模型承载板试验p-l曲线

图7-31　土工格室沙模量-格室深度曲线

注：所用土工格室的格室边长均为20cm

图7-32　土工格室沙模量-格室边长曲线

注：所用格室深度均为20cm

比较图中深度为15cm和20cm的点可以看出，格室深度增大，模量略有提高。从表7-10和表7-11可知，提高的幅度至多为2.585MPa，即仅提高1.12%。因此在给定条件下，可以认为格室深度的变化并不影响土工格室沙的抗压回弹模量。

图7-32表示了模量（平均值）与格室边长的关系。从图中可以看出，模量随格室单元的增大略有减小，其幅度在0.696～5.525MPa。可见这种影响也是很小的。但从图中曲线看，模量减小的趋势是稳定的，从表7-12的平均值一栏也能看出这一变化趋势。因此可以说，在给定条件下，格室单元的增大对土工格室沙的模量略有影响，模量有所减小，但不显著。

要分析这一现象的原因，可以从格室单元尺寸与承载板直径的相对关系入手。从极端意义上看，将格室单元边长从20cm增至无穷大，则模量必定从一定值减至沙基模量。因此模量减小的趋势是确定的。至于格室单元边长从20cm增至25cm和30cm，虽然格室单元有所增大，但相对于30cm承载板而言，这种变化并未引起承载板直径与格室单元边长间相对关系的质的变化，两者间的关系仍是处于承载板既不能完全覆盖格室单元，也不能完全放入格室单元的状态。因此模量的变化不应有大的跳跃。这样，其结果必然是模量有所减小，但无显著变化。

③土工格室对风积沙的加固作用是明显的。首先，从室内模型测试结果看，土工格室沙与沙基模量平均值之比见表7-13，土工格室沙模量显著高于沙基模量，说明土工格室对沙有明显的加固作用。

表7-13　土工格室沙与沙基模量之比（室内试验）

当然，土工格室对风积沙的加固程度是相对的，格室规格的改变也会导致加固效果的变化。显然，格室单元增大势必引起加固作用减弱。当格室单元的深度减小到一定程度，也可能使得剪切滑动面深入到沙基中，导致路面结构破坏，这时论及土工格室对沙的加固作用也就没有实际意义。由于该课题是针对工程实际进行研究的，试验限制在可能实际应用的格室规格范围，因此要在更大范围中认识土工格室的加固作用，尚需扩大试验规模，进一步研究。

④土工格室加固沙的抗压回弹模量。从试验结果可知，模型试验中，按三层体系反算的模量值与按二层体系反算的模量值也有差别。比较模型试验结果（表7-10和表7-11）可知，按三层体系反算的模量比按二层体系反算的模量高。这并非土工格室加固沙这种材料的固有特性，主要是由试验条件的差异引起的。由于土工格室沙是在干燥状态下碾压，其表面总是无法压实的，虽然上覆砂砾碾压后可以使土工格室沙表面压实，但砂砾将压入土工格室单元少许（根据观察模型试验，压入深度一般在0～2cm，但由于开挖时造成沙的扰动及砂砾和沙不易区分，这种界限不清晰），开挖后仍需填一层沙方能补平。这样无论测定的是两层结构还是三层结构，在土工格室沙表面测试，结果都会偏小。即为按二层体系反算的模量取用是偏于安全的。

通过以上分析，土工格室沙抗压回弹模量取值见表7-14。

表7-14　土工格室加固风积沙抗压回弹模量建议值