GNSS基准站网数据处理方法与应用：基准转换方法

基准变换是指在不同的参考基准间进行变换。转换方法有很多，包括三参数法、四参数法、七参数法和多项式逼近法等。

不同的数学模型有各自不同的假设前提，实际应用中采用哪种模型比较合理，以及在同一模型中取哪几个参数比较适宜，要根据卫星网和地面网的实际情况和转换的精度要求等因素综合决定。

1.三参数法

设两个空间大地直角坐标系为OB-XBYBZB和OA-XAYAZA，且两坐标系各坐标轴相互平行，仅坐标原点不一致，则可通过三参数法按照式(8-12)实现两坐标系的转换。

式中，ΔX0、ΔY0、ΔZ0为A坐标系原点相对于B坐标系原点在三个坐标轴上的分量，一般称为三个平移参数。

三参数法是在假设两坐标系间各坐标轴相互平行的条件下导出的，实际情况中往往并不可能。当欧拉角本身不大，且其误差和本身数值属同一量级时，可如此近似处理。例如，北美坐标系相对于地心坐标系的三参数为ΔX0＝-22m，ΔY0＝157m，ΔZ0＝176m；欧洲坐标系相对于地心坐标系的三参数为ΔX0＝-84m，ΔY0＝-103m，ΔZ0＝-127m等。

2.七参数法

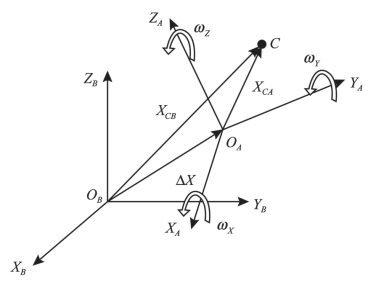
若两个空间大地直角坐标系间除了三个平移参数外，各坐标轴之间存在三个欧拉角，称为三个旋转参数，且两个坐标系尺度不尽一致，即存在一个尺度参数，那么这两个坐标系之间的转换可通过七参数法(三个平移参数、三个旋转参数和一个尺度参数)实现，如图8-4所示。

空间直角坐标系A到空间直角坐标系B的七参数转换关系为：

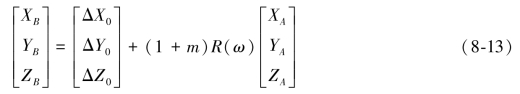
式中，(XA，YA，ZA)T为某点在空间直角坐标系A的坐标；(XB，YB，ZB)T为该点在空间直角坐标系B的坐标；(ΔX0，ΔY0，ΔZ0)T为空间直角坐标系A转换到空间直角坐标系B的平移参数；(ωX，ωY，ωZ)为空间直角坐标系A转换到空间直角坐标系B的旋转参数；m为空间直角坐标系A转换到空间直角坐标系B的尺度参数。

七参数法一般有三种公式，分别是布尔莎公式、莫洛琴斯基公式和范士公式，三者是相互等价的。实际应用中，可以舍弃那些不显著的参数，例如个别欧拉角，即选择四、五、六个参数来进行不同空间大地直角坐标系的转换，也就是所谓的四参数法、五参数法以及六参数法。

(www.xing528.com)

图8-4　七参数转换示意图

3.不同大地坐标系的转换

不同大地坐标系的换算，除了空间直角坐标系换算涉及的七参数外，还应增加两个转换参数，即两种大地坐标系所对应的地球椭球参数不同，转换公式为式(8-14)。不同大地坐标系的换算公式又称大地坐标微分公式或者变换椭球微分公式。当包括旋转参数和尺度变化参数时，称为广义大地坐标微分公式或者广义变换椭球微分公式。

式中，B为大地纬度，L为大地经度，h为大地高；ΔL″、ΔB″、Δh″为新旧坐标系换算量；，M＝N/V2，N＝a/W，a为椭圆的长半轴，e为椭圆的第一偏心率，e′为椭圆的第二偏心率；ρ＝206265″/弧度；ΔX0、ΔY0、ΔZ0为平移参数；εX、εY、εZ为旋转参数；m为尺度变化参数；Δa、Δf为地球椭球元素变化参数。

4.平面坐标系之间转换

平面坐标系之间的相互转换实际上是一种二维转换。一般而言，两平面坐标系之间包含四个原始转换因子，即两个平移因子、一个旋转因子和一个尺度因子。转换方法包括两种：

①先旋转，再平移，最后统一尺度。

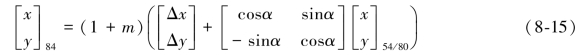
②先平移，再旋转，最后统一尺度。

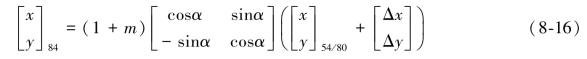
5.其他方法

七参数公式属于相似变换公式。由于地面网不可避免地存在系统误差，因此仅采用相似变换公式就显得不够完善，从而产生了多于七参数的各种转换公式，如九参数的霍丁公式，十参数的克拉克威斯基-汤姆森公式等。这类公式中，引入两组旋转参数：一组用于表示坐标系间由于轴的指向定义不一样带来的旋转参数，另一组用于说明地面网存在的系统误差。二者形式上相似，在一定条件下用于坐标转换和布尔莎公式等也是等价的。

当网的系统误差较为复杂时，使用多项式逼近法或者回归方程都可以完成坐标系间的转换。