GNSS基准站网数据处理方法与应用的数据分析与讨论

1.噪声模型对速度及速度不确定度的影响

以SOPAC提供的速度及速度不确定度为基准，比较未计算环境负载改正前确定的测站分量最优噪声模型下的速度及速度不确定度值与SOPAC的差值，相同及不同噪声模型下各测站分量的速度及速度不确定度差值分布如图7-9所示。

从图7-9(a)、图7-9(b)可以看出，就相同的FN＋WN模型而言，结果与SOPAC基本一致。83%的速度差值小于0.2mm/a，N、E方向最大为0.16mm/a，个别测站U方向最大达到0.58mm/a；78%的速度不确定度差值小于0.04mm/a，N、E方向最大为0.08mm/a，个别测站U方向最大为0.17mm/a。考虑舍入误差的影响，可以认为计算得到的结果是合理可靠的。另外，得到的FN＋WN模型下N方向的速度全部小于SOPAC提供的速度，E、U方向则没有这个特点，其原因可能是由于CATS软件和SOPAC数据处理方式的差异造成的(例如二者对阶跃性突变的处理方式)。

从图7-9(c)、图7-9(d)可以看出，相对于FN＋WN模型而言，不同的复杂噪声模型对测站速度及不确定度会产生一定的影响，U方向影响最大，E方向次之，N方向最小。40%的测站分量对应于不同噪声模型的速度差值小于0.1mm/a，47%的分量差值约为0.1～0.3mm/a，13%的测站U分量与SOPAC提供的速度差超过1mm/a；速度不确定度受不同噪声模型的影响量级约为亚毫米(0.1～0.8mm/a，占分量总数的87%)，少数U分量差值＞1mm/a(占分量总数的13%)。由此可以得出结论，对于mm级高精度参考框架的建立及板块运动分析来说，我们需要顾及不同噪声模型带来的这种差异。由于仅采用了中国区域11个IGS基准站的数据分析测站的噪声特性，仅能反映复杂噪声模型和FN＋WN模型获得的速度及不确定度差异量级，对于不同模型获得的速度不确定度较FN＋WN模型的优越性(即哪种模型获得的不确定度更接近测站的实际状况)还需要采用更多测站数据进行验证。

图7-9　相同及不同噪声模型下测站分量速度及其不确定度与SOPAC的差值

((a)、(b)：相同模型，(c)、(d)：不同模型)

2.环境负载对噪声模型的影响

理想情况下，GPS测站位置时间序列的噪声特性应表现为纯白噪声，然而实际情况下并非如此。从7.6.3可知，中国区域IGS基准站坐标时间序列表现为有色噪声特征。通常认为地球物理效应及与GPS技术相关的系统误差是产生有色噪声的潜在来源。为了分析计算的四种环境负载对IGS基准站噪声模型的影响，表7-2列出了负载改正前后11个基准站N、E、U分量的最优噪声模型。

表7-2　环境负载改正前后各测站分量的最优噪声模型比较

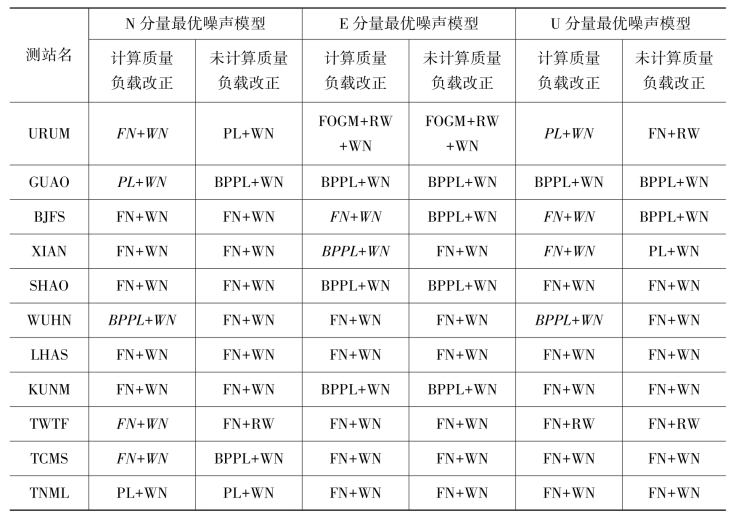
注：斜体部分表示计算地表负载改正后最优噪声模型发生变化的测站分量。

从表7-2可以看出，经地表负载改正后11个测站分量的噪声特性发生了变化(占总数的33%)，主要体现在N、U分量，E分量受到的影响较小。噪声类型的变化因站而异，并无显著规律，例如BJFS站的E、U分量经负载改正后带通噪声减小，而WUHN站的N、U分量的噪声特性却由原来的FN＋WN表现为BPPL＋WN。由此看来，环境负载对测站坐标时间序列的影响不可忽视(尤其是N、U分量)，为了能对其噪声特性进行准确分析，需要考虑其影响。

经负载改正后FN＋WN模型的比例有所增大(从51%增大到64%)，BPPL＋WN和FN＋RW＋WN模型比例减少，各测站分量的BP振幅(周期为0.5～1.5年)及RW振幅普遍出现变化。比较7.6.3得到的负载改正结果，可以认为计算的四种环境负载会引起除周年、半周年以外的谐波变化，对测站时间序列的影响可能表现为BP或者RW特性。考虑到负载模型的准确性以及采用测站数目的局限性，关于其确定影响还需做进一步深入研究。

3.环境负载对线性速度及不确定度的影响

表7-3列出了计算四种环境负载改正前后各测站分量最优噪声模型下的线性速度及不确定度，其速度及速度不确定度差值分布如图7-10所示。

表7-3　改正前后各测站分量最优噪声模型下的线性速度及不确定度比较

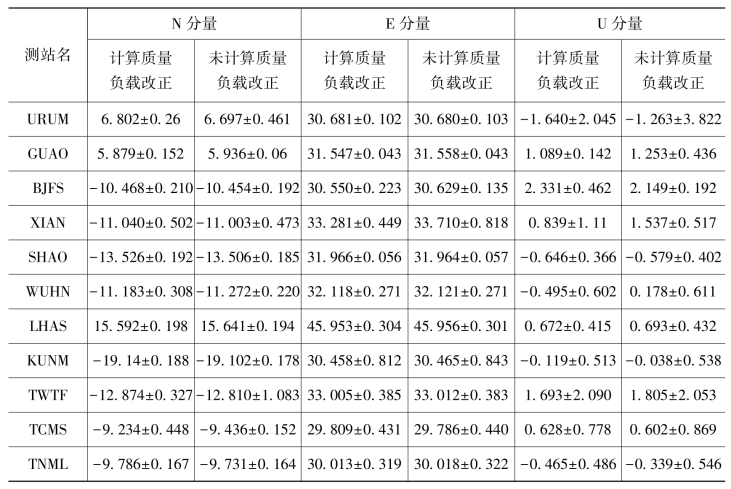
注：斜体部分表示计算环境负载改正后最优噪声模型发生变化的测站分量。

从表7-3及图7-10可以看出，整体来说，计算的四种环境负载对测站的速度及速度不确定度具有一定的影响。速度变化较小，30%表现为1/10mm/a量级，48%表现为1/100mm/a量级，22%表现为1/1000mm/a。其中，U分量最大，表现为1/10～1mm/a，N分量次之，为1/100～1/10mm/a量级，E分量最小，为1/1000～1/100mm/a量级。速度不确定度变化略小于速度变化，且范围更为集中，21%表现为1/10mm/a量级，39%表现为1/100mm/a量级，36%表现为1/1000mm/a量级。其中，N、U方向相当，为1/100～1/10mm/a量级，E分量最小，为1/1000～1/100mm/a量级；76%的测站速度(包括三个分量)表现出速度减小的现象，速度不确定度则没有显著增大或减小趋势。结合7.6.3的计算结果，可以认为，现有机构提供的测站线性速度成果可能不准确，其对应的速度不确定度同样可能不符合实际；环境负载会造成测站的线性速度及速度不确定度变化，U、N方向较大，E方向较小，速度变化最大达到0.7mm/a，不确定度变化最大甚至超过1.5mm/a，板块运动分析时需扣除其影响。(www.xing528.com)

4.环境负载对测站周年、半周年振幅的影响

为了研究计算的四种环境负载与中国区域IGS基准站周期振幅之间的关系，分别估计了不同噪声模型下考虑、未考虑质量负载影响的测站周年、半周年振幅，最优噪声模型下的结果如表7-4所示。

图7-10　环境负载改正前后全部测站分量速度及速度不确定度差值分布

表7-4　计算环境负载改正前后测站分量的周年、半周年振幅

续表

注：括号内数字表示SOPAC提供的周年、半周年振幅。

负载改正前后各测站分量的周年振幅及其变化随纬度分布如图7-11、图7-12所示。总体来说，不论计算质量负载改正与否，各测站运动均存在显著的周年振幅。未考虑负载影响时，U分量最大，为3～10mm，E分量次之，为1～5mm，N分量最小，为1～2mm，与Meisel等(Meisel，et al.，2009)结果一致。计算负载改正后，U分量周年振幅仍然最大，为1～10mm，N、E分量较小，为1～5mm，其中N分量周年振幅略大于E分量。所有测站N分量周年振幅全部变大，变化为0～2.8mm，E分量变化较为平缓集中，为-0.6～0.7mm，U分量除2测站分别增大4mm、2mm外，其余全部减小(80%)，为0.2～6.3mm，且变化较为剧烈。

图7-11　环境负载改正前后各测站分量周年振幅随纬度分布图

图7-12　环境负载改正造成的各测站分量周年振幅变化随纬度分布图

负载改正前后各测站分量的半周年振幅及其变化随纬度分布如图7-13、图7-14所示。从图中可以看出，各测站半周年振幅明显小于周年振幅。计算负载改正前，测站U分量半周年振幅较大，为0.4～2.1mm，E分量次之，为0.4～1.6mm，N分量最小，为0.1～1.2mm。负载改正后，U分量半周年振幅为1～3mm，E分量为0.4～1.7mm，N分量为0.1～1mm。U分量变化最大，为-1～2mm，N分量次之，为-0.5～0.5mm，E分量最小，为-0.2～0.2mm。

图7-13　环境负载改正前后各测站分量半周年振幅随纬度分布图

图7-14　环境负载改正造成的各测站半周年振幅变化随纬度分布图

由此可以得出结论，计算的四种环境负载确实会造成中国区域IGS基准站的周年、半周年运动，其影响因站而异，与测站周围地理环境相关，引起的周年运动较半周年运动幅度大，但是并不能完全减小GPS位置时间序列的周年、半周年振幅，尤其是半周年振幅。经质量负载改正后，73%的测站分量半周年振幅增大(某些测站U分量的增大量达1～2mm)，52%的测站分量周年振幅增大(包括所有测站N分量)，不过仅U分量而言，80%测站分量的周年振幅显著减小。也就是说，就中国区域IGS基准站而言，包括大气压负载、非潮汐海洋负荷、积雪深度和土壤湿度负载在内的四种环境负载对测站位置时间序列的贡献较少，主要表现为测站U分量的周年运动，但是并不能很好地解释测站的半周年运动以及水平方向的周年运动，相反会增大测站N分量的周年运动，我们需要从其他地球物理源(例如周日、半周日大气潮，海洋潮负载等影响)和系统误差源入手，进一步从本质上分析并确定测站的周期运动，为测站的非线性运动建模提供可靠的理论支持。