1.环境负载改正前最优噪声模型的确定
采用上文所说的数据处理策略,根据最优噪声模型评价准则,对选取的11个IGS基准站进行上述7种组合噪声模型分析,得到了计算质量负载改正前中国区域IGS基准站分量噪声特性的最优模型。图7-6给出了11个IGS站共33个分量的最优噪声模型分布。
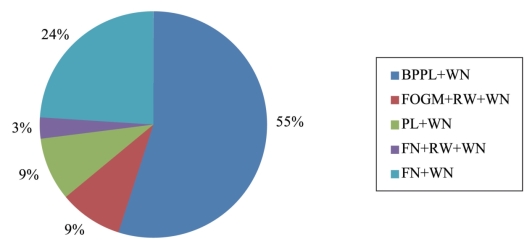
图7-6 计算环境负载改正前的中国区域IGS基准站分量最优噪声模型分布
从图7-6可以看到中国区域IGS基准站分量的噪声特性存在多样性,主要表现为FN+WN和BPPL+WN模型,其他复杂模型也占有一定比例。大部分测站的N、E、U分量表现出不同的噪声特性,因此寻找时间序列变化特征的物理解释时需对各分量区别对待。另外,地理位置相近测站的时间序列也可能具有不同的噪声特征(例如TNML、TCMS站N分量)。考虑到地球物理效应的空间相关性,有的测站可能存在有较大的系统误差。
此外,计算得到的各测站分量FN+VW模型的MLE值明显大于其他组合模型,与袁林果等(袁林果等,2008)的结果一致,但是我们认为VW模型仅能反映测站分量的质量好坏,并不能作为基准站的最优噪声模型。为了确保结果的可靠性,本节最优噪声模型的确定不考虑FN+VW模型。
2.环境负载造成的测站位移
就季节性尺度来说,环境负载引起的测站位移是GPS位置时间序列的主要特征(Langbein,et al.,1997)。为了分离地球物理效应的影响,通常采用Farrell格林函数与独立环境负载数据的卷积计算不同质量负载引起的测站位移,然后从GPS时间序列里扣除这部分影响(Farrell,1972;Tregoning,et al.,2005;李英冰,2003;张诗玉,2004)。
采用QOCA软件计算了1995年1月1日—2010年4月1日期间大气压负载、非潮汐海洋负载、积雪深度及土壤湿度负载对中国区域11个IGS基准站的日位移影响。图7-7分别表示四种质量负载造成的SHAO站N、E、U方向的日位移。(https://www.xing528.com)
从图7-7及其他测站的计算结果表明,不同环境负载对测站的影响均表现为U方向最大,N、E方向影响较小,与已有研究成果一致(王敏等,2005;袁林果等,2008;朱文耀等,2003)。部分质量负载对测站的影响与其地理环境密切相关,同一测站对不同质量负载的敏感度也不同。就选取的11个IGS基准站而言,土壤湿度负载造成的测站位移最大,大气压负载、非潮汐海洋负载次之,积雪负载对测站位移的影响最小,且随纬度降低而减小。
3.环境负载改正后最优噪声模型的确定
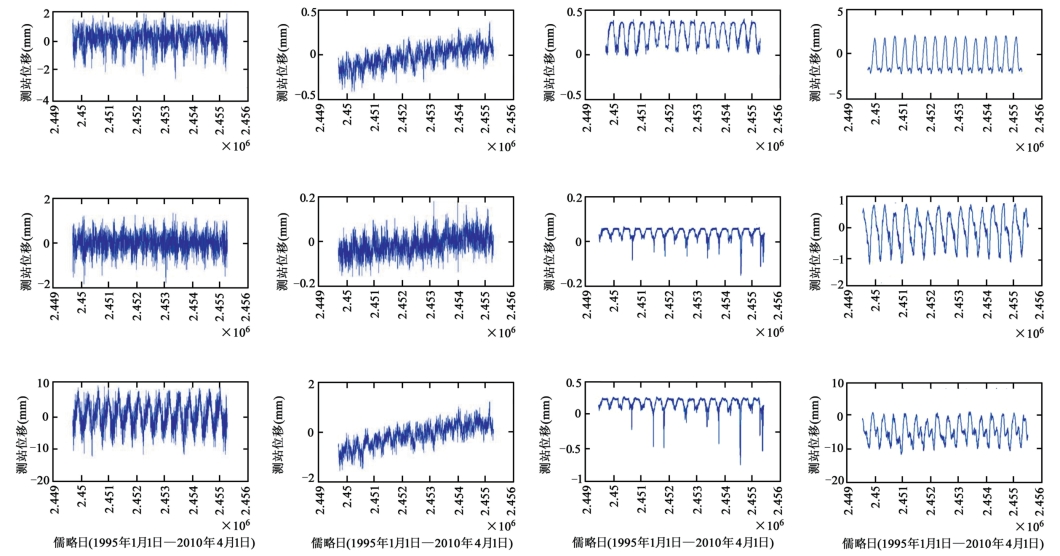
图7-7 不同质量负载造成的SHAO站N、E、U(上、中、下)方向位移
(从左至右依次为大气压负载、非潮汐海洋负载、积雪深度负载及土壤湿度负载)
根据上述计算结果对中国区域11个IGS基准站N、E、U方向的位移进行地表质量负载改正,并对改正后的坐标时间序列重新进行噪声分析,我们得到了适合于扣除地表质量负载影响后的中国区域IGS基准站分量最优噪声模型。图7-8表示各测站分量所属最优噪声模型的比例分布。与图7-6相比,计算环境负载改正后FN+WN模型的比例有所增大,BPPL+WN和FN+RW+WN模型比例减少。
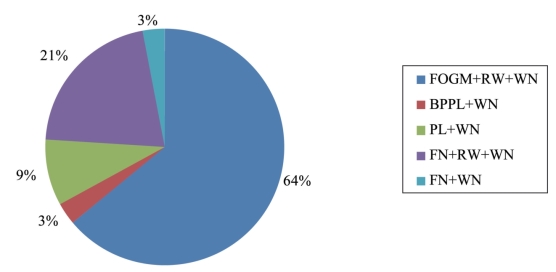
图7-8 计算环境负载改正后的中国区域IGS基准站分量最优噪声模型分布
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




