最优环境负载模型的建立及分析

GGFC和QOCA均可以计算环境负载(包括大气压负载、非潮汐海洋负载以及水文负载)。GGFC和QOCA最大的差异在于水文负载输入数据的不同。GGFC根据GLDAS模型获得的月均雪水当量及土壤湿度值计算陆地储水量变化造成的地表位移，而QOCA的水文负载输入数据为NCEP再分析数据提供的积雪深度及土壤湿度。这些数据集代表了不同精度的环境负载模型，对负载效应的评价具有直接的影响。采用不同的质量负载数据计算得到的垂直位移可能不相同。比较不同数据源获得的环境负载效应的精度及差异有利于寻找更为有效的修正坐标时间序列非线性变化的方法。

GGFC采用全球格网内插的方式计算不同测站处的环境负载效应。这种情况下，插值误差会传播至测站的负载时间序列，造成计算得到的负载效应与实际估值的偏离。为了消除这种偏差，我们根据地球弹性形变理论，采用Farrell格林函数与全球地表质量分布做卷积获得给定测站的负载效应，将该方法获得的负载位移时间序列称之为最优模型数据(Optimal Model Data，OMD)，包括最优水文负载时间序列(optimal continental water storage，cws_optimal)、最优非潮汐海洋负载时间序列(optimal ocean bottom pressure，obp_optimal)及最优大气压负载时间序列(optimal atmospheric pressure loading，atml_optimal)。其中，对于atml_optimal，我们采用经地形改正的高分辨率地表气压数据代替原始的NCEP数据计算大气压负载造成的测站位移，以降低复杂地形及较低空间分辨率导致的气压数据偏差影响(Jiang，et al.，2013；李昭，2012)。

我们选取了同一组GPS高程时间序列，研究分析了3种(GGFC、QOCA、OMD)不同环境负载建模方法的改正效果。通过对不同数据源的负载数据以及坐标时间序列预处理之后，对获得的环境负载位移和高程时间序列进行了组合。组合分两步：第一步分别计算三种不同数据源得到的负载效应和造成的测站垂直周位移时间序列；第二步对于所有选择的IGS基准站将三种数据源得到的负载和分别内插至GPS周时间序列的观测时刻，由此即可获得将环境负载改正后的GPS高程周时间序列。图7-1给出了233个IGS基准站的总负载绝对值的平均值空间分布，图中不同颜色代表不同位移量，白色圆圈表示该测站的负载位移大于对应的色标。总体而言，就同一测站来说，OMD计算得到的负载值最小，GGFC次之，QOCA最大。不论采用哪种方法，负载造成的垂直位移均与温度带密切相关。最大的负载信号位于温带及寒带地区(中高纬度，通常大于2mm)，且主要集中在北温带；温带及热带区域的负载效应最弱(中低纬度，小于2mm)，尤其是热带地区。负载效应同样与测站距海洋的临近程度有关。相同纬度下，位于辽阔大陆中心的测站受环境负载的影响(大于2mm)大于临近海岸线的测站(小于1mm)。由此我们可以认为，对于mm级参考框架的建立，环境负载对IGS基准站的影响不可忽视，尤其对于北半球中高纬度及远离海洋的测站更是如此。

图7-1　三种负载效应造成的垂直位移绝对值的平均值空间分布

(上：QOCA，中：OMD，下：GGFC)

图7-2给出了选取的233个IGS基准站的原始高程及其经三种不同环境负载建模方法改正后的周时间序列。图中，黑线表示原始GPS周时间序列，绿线代表QOCA改正后结果，蓝线表示GGFC改正后结果，红线代表OMD改正后结果。右图红色圆圈表示不同温度带内本文采用的测站分布，4个测站的名称及位置采用黑色字体标示。考虑到负载效应与温度带的相关性，这里仅给出每个温度带内2个测站的组合结果。从图中可以清楚看到，环境负载模型确实能够解释部分GPS非线性变化，且负载效应因站而异。不同方法计算得到的同一测站处的负载效应同样各不相同，尤其是对于北半球的测站，例如ankr、nya1。除此以外，图7-2还表达了一个明显的特征：QOCA负载改正值与原始GPS高程时间序列的符合程度次于其余两种数据源。

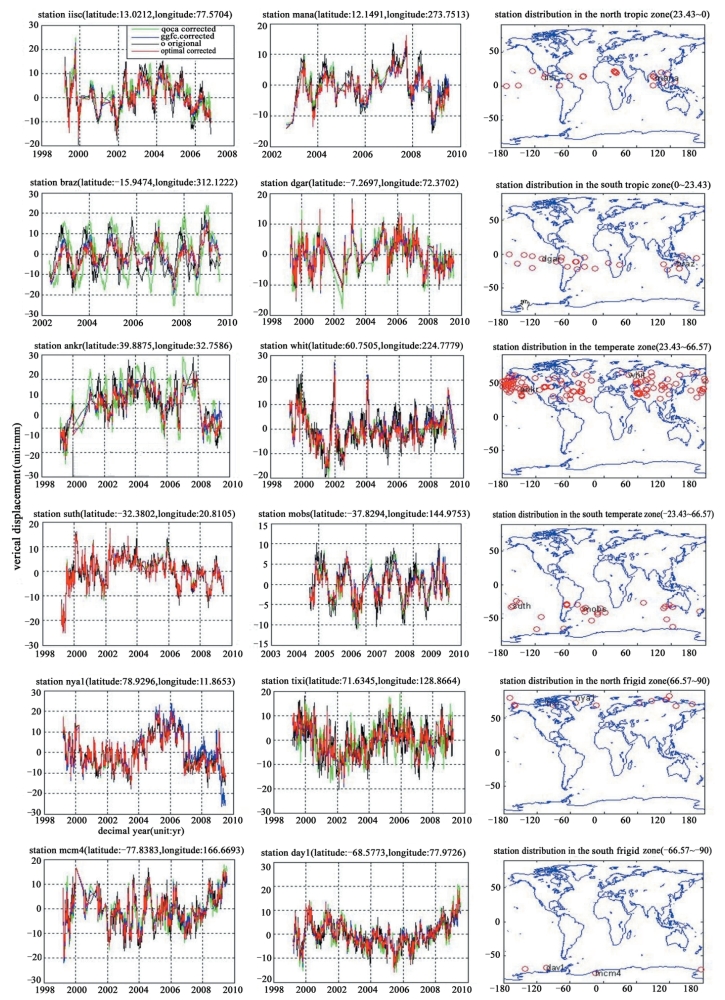
图7-2　环境负载改正前后测站高程时间序列变化及选取的IGS基准站

为了进一步评估采用不同环境负载建模方法对GPS坐标时间序列的影响，分别计算了三种建模方法得到的负载改正前后GPS周时间序列的RMS差。

图7-3、图7-4分别描述了根据三种环境负载时间序列计算得到的RMS差的二维和三维空间分布。OMD的改正效果最好，GGFC次之，QOCA较差。三种负载时间序列改正获得的RMS差与经度分布、负载RMS及GPS原始时间序列的RMS均不相关。(www.xing528.com)

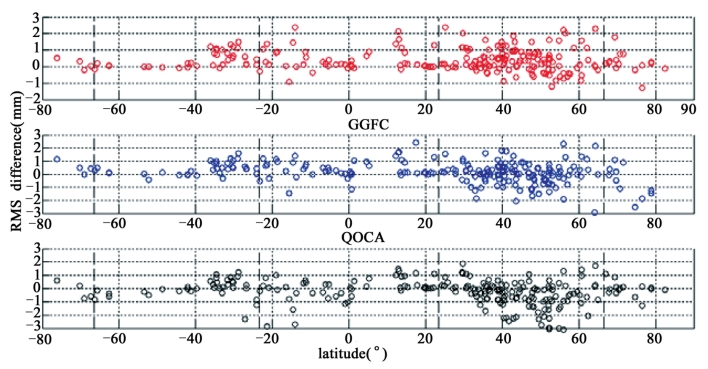
图7-3　三种负载模型获得的RMS差随纬度分布图

(上：OMD，中：GGFC，下：QOCA)

采用OMD负载改正后，全球172个IGS基准站(占233个测站的73.8%)高程时间序列的RMS减小(图7-2(上)、图7-3(中))。不论南北半球、热带及温带区域多数测站的RMS减小，最显著的改正效果(RMS差＞1mm)聚集在亚洲、大洋洲、北美以及南美的少数测站。就RMS增大的测站来说，负值绝对值较大的测站主要集中在纬度约大于40°的北温带(尤其是欧洲区域)。由此推测该区域可能存在某种未模型化的地球物理现象，例如基岩热膨胀等因素的影响，但仍需进一步分析验证。造成RMS增大的另外一个可能主要原因是GPS数据处理策略的不完善，如未模型化的高阶电离层延迟及S1-S2大气潮汐造成的不同区域测站坐标估值偏差与环境负载效应的相互作用。RMS增大的测站中，仅2个测站的RMS增大量大于1mm(thu1，格陵兰；wsrt，荷兰)。Thu3及thu1站为并置站，二者的负载时间序列几乎相同，其RMS差却存在显著差异，分别为0.07及-1.30，由此推断thu1站的RMS差的增大主要由GPS技术误差引起而非环境负载效应。

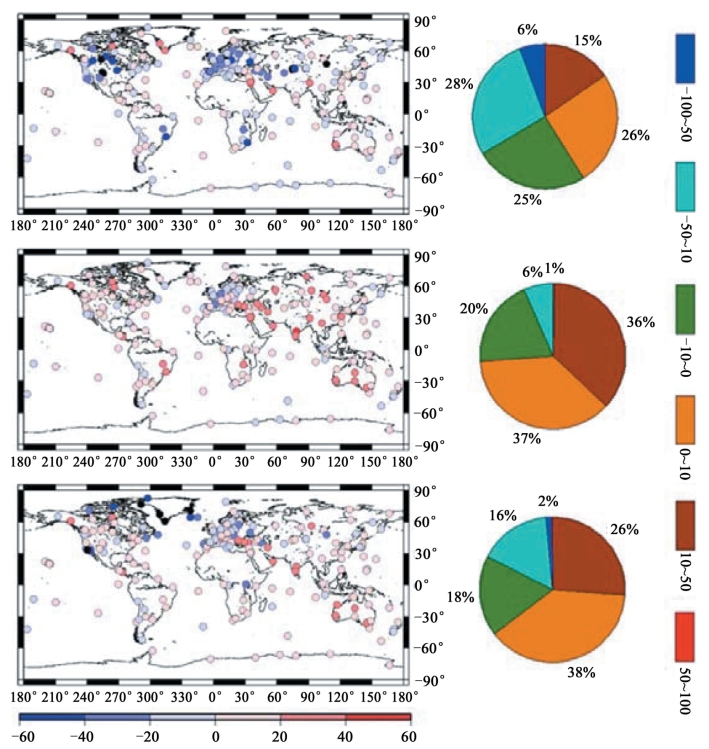
图7-4　三种负载模型获得的RMS差全球分布图

(上：QOCA，中：OMD，下：GGFC)

由图7-3和图7-4的结果看，GGFC的改正效果略逊于OMD，63.5%的测站经GGFC负载改正后RMS减小。由于GLDAS模型的缺陷，负载改正使得位于格陵兰的测站及北极部分测站的RMS增大，应避免采用GGFC模型修正该区域的GPS坐标时间序列。根据GGFC模型得到的全球其他区域测站的RMS差与OMD表现为几乎相同的分布趋势，只不过对于同一区域，OMD的改正效果较GGFC相比更为显著，其原因主要在于OMD采用了经地形改正的高分辨率气压数据。另外，OMD直接计算特定位置的负载效应，而GGFC采用内插的方法，插值误差可能导致环境负载结果的偏差。尽管如此，经GGFC负载修正后的南极洲IGS基准站的RMS全部减小，而OMD则没有这种优势，造成这种异常的原因可能源于该区域的地形误差。就GGFC负载改正结果与温度带的相关性而言，热带、南温带及南寒带多数测站的RMS经GGFC改正后减小，北温带及北寒带区域多数测站却经GGFC负载改正后RMS增大。就区域而言，RMS减小的测站主要聚集在北美、南非、亚洲、大洋洲及南极洲，而RMS增大的测站除格陵兰及北极外主要位于欧洲区域。

与GGFC、OMD相比，QOCA的负载改正效果不是很理想，仅能使得41.2%的全球IGS基准站RMS降低(96/233)，且RMS差值与温度带或南北半球均无相关性。实施QOCA负载改正后，北美、南美、欧洲、亚洲、南非及南极洲的多数测站RMS增大，尤其是北美中部及亚洲中部区域。除大洋洲外，RMS减小的多数测站位于陆海交界处或者海洋区域。虽然QOCA直接计算每个测站的负载效应，而GGFC采用内插的方法，对于选择的GPS数据来说，QOCA的负载改正效果不如GGFC。笔者认为造成此差异的原因可能有：ATML、CWS负载建模采用的不同输入数据及CE与CF框架的近似。考虑到CE与CF的微小差异，笔者认为QOCA负载改正结果不理想的主要原因在于NCEP提供的气压及水文数据的不准确。

总之，三种方法获得的负载效应因站而异，OMD的改正效果最好，GGFC次之。OMD得到的负载位移时间序列的RMS最小(小于7mm)，GGFC次之(除格陵兰地区的异常值外，最大RMS为8.9mm)，QOCA最大(RMS达12.2mm)。不同方法获得的负载RMS均随纬度升高而变大，且在相同的温度带内表现为相同的变化趋势。环境负载造成的地表位移能够解释部分GPS非线性变化，不论采用哪种方法，尤其是对于北半球中高纬度地区的IGS基准站的影响不可忽视。