根据SOPAC给出的IGS基准站坐标改进函数模型,采用正弦、余弦函数描述测站的年周期、半年周期变化,将测站沿N、E、U方向的运动按照下式建模。
式中,t表示单天坐标解历元,以年为单位;a为测站位置,b为线性速度;系数c,d描述测站的年周期运动;e,f描述半年周期运动;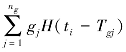 为跳变改正项,其中gj表示跳变振幅,Tgj表示发生跳变的历元,ng表示跳变个数,H为海维西特阶梯函数(Heaviside Step Function),在发生突变前H值为0,发生突变后H值为1;vi为观测噪声。这里的跳变时刻经分析确定后作为已知,因此模型是各项系数的线性函数,待求参数为:
为跳变改正项,其中gj表示跳变振幅,Tgj表示发生跳变的历元,ng表示跳变个数,H为海维西特阶梯函数(Heaviside Step Function),在发生突变前H值为0,发生突变后H值为1;vi为观测噪声。这里的跳变时刻经分析确定后作为已知,因此模型是各项系数的线性函数,待求参数为:
运动方程可表示为:
式中,A为参数的系数矩阵。若观测噪声为非相关白噪声,观测值协方差阵由日坐标解的独立方差![]() 定义:
定义:
取单位权方差为1,根据加权最小二乘解原则,可得未知参数的最优线性无偏估计值为:
参数的协方差为:
![]() 为输出协方差阵的比例因子,采用下式计算:(https://www.xing528.com)
为输出协方差阵的比例因子,采用下式计算:(https://www.xing528.com)
式中,N表示日坐标解的个数;t为模型参数的个数。
拟合残差为:
为了避免舍入误差引起的数值不稳定,方程(7-13)的最小二乘解可以采用正交三角分解(或者称“QR分解”)求得:
式中,Q为正交矩阵;R为非奇异上三角矩阵。于是参数的最小二乘估值可写为:
参数协方差阵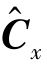 用于检验引入的坐标突变参数显著性,把估计出来的突变值和估计误差进行比较。如果估计的突变值小于一倍中误差,则认为该参数不显著,应从模型中去除。若跳变时刻已知,该步骤通常可以省略。为了确保所求参数的准确性,可根据显著性检验结果对模型进行多次迭代。初次模型参数求解完成后,采用相关算法对拟合残差
用于检验引入的坐标突变参数显著性,把估计出来的突变值和估计误差进行比较。如果估计的突变值小于一倍中误差,则认为该参数不显著,应从模型中去除。若跳变时刻已知,该步骤通常可以省略。为了确保所求参数的准确性,可根据显著性检验结果对模型进行多次迭代。初次模型参数求解完成后,采用相关算法对拟合残差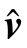 进行分析,剔除粗差影响。然后对剔除粗差的观测数据重建模,求得“净化”的噪声时间序列(即拟合残差
进行分析,剔除粗差影响。然后对剔除粗差的观测数据重建模,求得“净化”的噪声时间序列(即拟合残差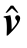 )。
)。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




