传统PPP技术是基于相关参数域信息的精密定位模式。由于利用较大范围覆盖的少量测站数据即可确定GNSS卫星的各类参数域误差改正信息(如卫星轨道误差、卫星钟差等),因此在实际中对参考网的选取密度没有很高的要求,通过一定时间的收敛(如30min)可以提供全球范围内双频接收机静态5cm、动态15~20cm的精密定位服务。
载波相位观测值中存在的接收机和卫星硬件延迟,使其模糊度不再具有整数特性,因此需要较长的收敛时间。最近的研究表明,通过一定的技术手段消除之前一直被忽略的接收机和卫星硬件延迟,可进一步实现非差或星间单差观测值的模糊度快速收敛,从而使PPP模式快速精密定位成为可能(Collins,2008;Ge,et al.,2008;Laurichesse,et al.,2007)。Ge等人(2008)在分析全球IGS跟踪站观测数据时发现,双差模糊度固定的成功率高达97%,且双差模糊度是由两个台站的星间单差模糊度组合而成,对于不同测站,其星间单差模糊度应具有近似相等的小数部分。基于这一思想,可以利用参考网估计星间单差模糊度的小数部分即星间单差硬件延迟,实现用户端单差模糊度的有效固定。Laurichesse(2007)与Collins等人(2008)方法的基本思想都是将星间单差模糊度的小数部分通过修正卫星钟差的方式发送给用户。由于需要向用户提供一套独立于IGS精密钟差的卫星钟差产品,所以适用范围较为有限。
无论是传统的PPP技术,还是改进后的PPP模糊度固定技术,都是基于参数域的改正信息实现精密定位服务。参数域的误差改正信息更加近似于对应误差的最优修正值,可以更好地反映误差的物理特性。然而,由于载波相位观测值波长(L1波长约为19cm,L2波长约为24cm,LW波长约为86cm)以及伪距观测值精度(C/A码为3m,P码为3~5dm)的限制,需要通过多个历元的载波相位观测值对伪距进行平滑才可能利用平滑后的伪距观测值正确固定相位模糊度,所以传统PPP模式的模糊度收敛较慢。此外,因为参数域的误差改正方式难以对电离层、对流层延迟误差进行精确建模,所以GNSS单频用户无法采用PPP模式进行精密定位。
网络RTK的各种方法本质上是一致的,只是误差改正模型的融合方法、数据播发方式以及侧重点略有不同,在此以综合误差内插法为例对网络RTK技术进行说明。
与PPP技术在参数域对各类误差进行描述相比,网络RTK技术则是根据用户站与参考站间误差的相关性,在观测值域利用主参考站数据对误差进行代替以保持用户站模糊度的整数特性,实现网内用户采用不同类型观测值(L1、L2、LW)的快速精密定位。原本存在于参数域的各类误差在不同测站处的影响是不一样的,而网络RTK技术在建模时将其简化为随测站位置线性变化,参数域误差中不满足线性变化的部分会随着参考网的扩大而增加。当这部分误差大到一定程度时便会影响用户站模糊度的解算,因此网络RTK技术一般仅适用于区域网建模,且需要较高的数据更新率。此外,网络RTK模式在数据处理时需要提供主参考站的观测数据,采用相对定位模式进行解算,远离参考网的用户将不再适用于该数据处理模式。
为了综合PPP技术与网络RTK技术各自的优点,可基于非差模式构造一种误差模型化方法,采用现有的各类卫星轨道和钟差产品,实现对全球PPP与区域RTK在技术上的统一和服务上的无缝连接(Ge,et al.,2010),使网内和网外用户基于同一种数据处理模式(PPP模式)获得不同精度需求的精密定位服务:网内接收到区域误差改正信息的用户站可获得与网络RTK模式相等价的快速、精密定位结果,而网外或未接收到该区域误差改正信息的用户则得到PPP模式的定位精度(邹璇,2010)。
基于非差改正数的网络RTK方法需要精确估计区域电离层和对流层延迟,并通过提供观测值域的各类误差改正信息实现PPP模式的快速精密定位(Ge,et al.,2010)。GNSS载波相位观测方程如下:
![]()
式中,s为卫星编号;r为接收机编号;![]() 为伪距观测值;
为伪距观测值;![]() 为接收机r和卫星s之间的几何距离;c为真空中光速;δtr和δts分别为接收机和卫星钟差;bP,r和
为接收机r和卫星s之间的几何距离;c为真空中光速;δtr和δts分别为接收机和卫星钟差;bP,r和![]() 分别为伪距观测值在接收机和卫星处所受的硬件延迟;
分别为伪距观测值在接收机和卫星处所受的硬件延迟;![]() 为卫星轨道误差;
为卫星轨道误差;![]() 为信号所受的对流层延迟影响;
为信号所受的对流层延迟影响;![]() 为信号所受的相对论效应影响;
为信号所受的相对论效应影响;![]() 为信号所受的电离层延迟影响;
为信号所受的电离层延迟影响;![]() 为模型改正残余项及伪距观测值噪声;
为模型改正残余项及伪距观测值噪声;![]() 为载波相位观测值;λ为相应的载波波长;
为载波相位观测值;λ为相应的载波波长;![]() 为该测站卫星对载波相位观测值的整周模糊度;bL,r和
为该测站卫星对载波相位观测值的整周模糊度;bL,r和![]() 分别为载波相位观测值在接收机和卫星处所受的硬件延迟;
分别为载波相位观测值在接收机和卫星处所受的硬件延迟;![]() 为模型改正残余项及载波相位观测值噪声。
为模型改正残余项及载波相位观测值噪声。
此外,载波相位观测值还受到其他一些误差的影响,如天线相位中心偏差和变化,相位缠绕等。(https://www.xing528.com)
对于参考网内的每一颗可视卫星,由于其轨道误差与测站位置相关,而卫星钟差和硬件延迟对全部测站是一致的,故而可在观测值域对这几类可能影响模糊度固定的误差一并建模。因此,无论采用何种卫星轨道(IGS精密卫星轨道或者广播星历卫星轨道)或卫星钟差(IGS精密钟差、广播星历卫星钟差或利用区域参考站网估计的卫星钟差)产品,用户以基于非差改正数的网络RTK方法按照PPP模式进行精密定位均可获得一致的定位结果。与传统单层模型和Klobuchar模型等经验函数模型相比,基于非差改正数的网络RTK方法是利用参考站实测数据对每颗可视卫星分别建模。如图5-14所示,将全部参考站用Delaunay方法划分为若干三角子网,按照基于非差改正数的网络RTK方法分别对各子网构建每颗可视卫星的误差改正模型。构建模型类似于一个以卫星为顶点,各参考站为底面的倒棱锥形,且对卫星方向的一小块区域进行建模,这一建模思想可以有效模型化局部范围内的电离层和对流层扰动。由于对每颗卫星方向的电离层、对流层,以及与卫星相关的硬件延迟、卫星钟差、卫星轨道误差都被精确构建到区域误差改正模型中,此时将由基于非差改正数的网络RTK方法提供的误差改正信息记为![]() ,则有:
,则有:
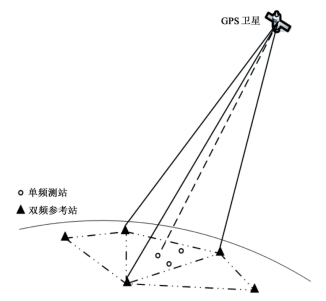
图5-14 基于非差改正数的网络RTK方法模型构建示意图
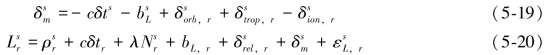
式(5-20)的载波相位非差观测方程中,除了待求的载波相位模糊度(![]() ),仅剩下接收机硬件延迟(bL,r)和接收机钟差(δtr)未知。为此对式(5-20)做星间单差。由于观测噪声的星间单差(
),仅剩下接收机硬件延迟(bL,r)和接收机钟差(δtr)未知。为此对式(5-20)做星间单差。由于观测噪声的星间单差(![]() )为一小量,在此忽略不计,此时有
)为一小量,在此忽略不计,此时有
![]()
式(5-21)中除星间单差载波相位模糊度![]() 外各项均可以精确已知,因此当网内用户根据其近似测站坐标计算得到每颗卫星的误差改正信息
外各项均可以精确已知,因此当网内用户根据其近似测站坐标计算得到每颗卫星的误差改正信息![]() 并依此对观测值进行改正后,如式(5-21)所示,其星间单差载波相位观测值的模糊度
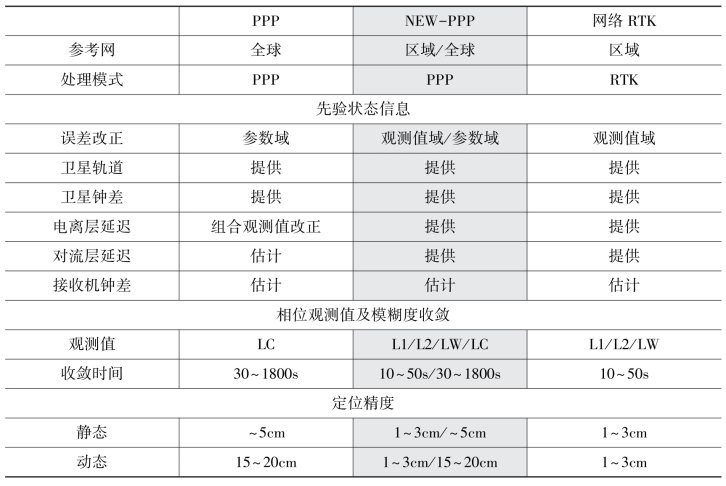
并依此对观测值进行改正后,如式(5-21)所示,其星间单差载波相位观测值的模糊度![]() 保持了整数特性,可以采用PPP模式实现快速精密定位(Ge,et al.,2010)。对于网外或无法获取区域误差改正信息的用户,由于是使用IGS提供的卫星轨道和钟差产品,因此可以按照同样的数据处理模式,采用传统PPP或星间单差模糊度固定方法(Ge,et al.,2008)实现精密定位。以基于非差改正数的网络RTK方法(参考网内)和星间单差模糊度固定方法(参考网外)实现全球无缝连接精密定位的这种定位模式在此暂且称为NEW-PPP,该项技术是对现有PPP与网络RTK技术的融合和统一,三类技术相互间的对比见表5-4。
保持了整数特性,可以采用PPP模式实现快速精密定位(Ge,et al.,2010)。对于网外或无法获取区域误差改正信息的用户,由于是使用IGS提供的卫星轨道和钟差产品,因此可以按照同样的数据处理模式,采用传统PPP或星间单差模糊度固定方法(Ge,et al.,2008)实现精密定位。以基于非差改正数的网络RTK方法(参考网内)和星间单差模糊度固定方法(参考网外)实现全球无缝连接精密定位的这种定位模式在此暂且称为NEW-PPP,该项技术是对现有PPP与网络RTK技术的融合和统一,三类技术相互间的对比见表5-4。
表5-4 PPP、NEW-PPP与网络RTK技术对照表
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




