GNSS基准站网数据的处理方法与应用分析

为了验证新的处理策略，我们在PANDA(Positioning And Navigation Data Analyst)软件的基础上实现了上述处理流程，并利用大量资料进行了计算。现将验证方法和结果介绍如下：实验采用2012年IGS全球观测站网年积日201至289的观测数据。期间约有460个IGS观测站的观测数据。首先，采用当前IGS处理策略对全球均匀分布的约100个测站进行精密定轨，以获取精密轨道、精密钟差和EOP等参数，并利用这些测站计算得到UPD。之后采用上述给出的新策略处理所有460个测站，并对其解算效率进行分析。测站分布如图4-9所示，其中，红色三角代表用来估计卫星精密轨道和钟差的核心站，蓝点代表是剩余的360个测站。

对每一天的数据按照4.5.2节的解算策略进行处理，并通过分析其时间序列来评估其稳定性。我们采用两种方式来进行最终的整网解，一种是仅采用载波距离观测值，一种同时采用载波距离和伪距观测值进行解算，为了简便，以下分别称之为方案A和方案B。在整网处理中，解算策略第一步中被强约束的测站此时仍然被施以强约束。然后通过轨道结果与IGS最终轨道的差异，以及相邻天之间重叠轨道平均偏差来验证新的处理策略。

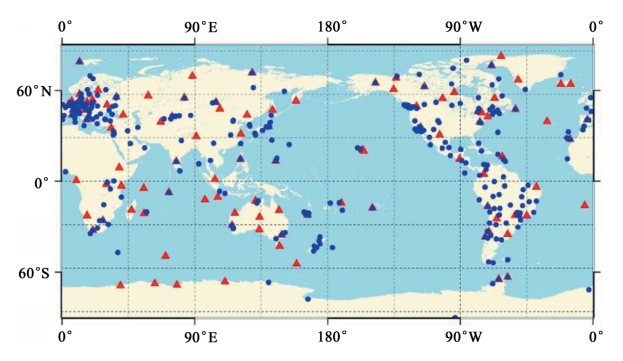
图4-9　测站分布图

为了验证新策略的计算效率，实验采用不同的解算策略对2012年年积日235天，包含不同测站数目的GPS网进行处理，比较分析其处理所需的时间。使用的解算策略除了上述的方案A和方案B外，还额外采用了葛茂荣等人提出的“参数消去法”作为比较，以下称为方案C。

1.UPD稳定性分析

由于宽巷波长较长，宽巷UPD(WLUPD)已被证明是相当稳定的，在此着重研究窄巷UPD(NLUPD)的稳定性。我们主要采用标准差来评估NLUPD的稳定性。如图4-10所示，红色三角展示了年积日239当天每颗GPS卫星的NLUPD的标准差，蓝色表示在年积日201到289内，去掉BLCOK IIA地影中的跳变后的平均标准差值。可以看到，除了G08和G09两颗卫星外，大体上其他各卫星NLUPD的标准差都很小，大多数都小于0.05周。去掉地影卫星的跳变后，所有卫星的平均标准差也基本上小于0.05周，这说明了卫星段NLUPD在一天内也十分稳定。

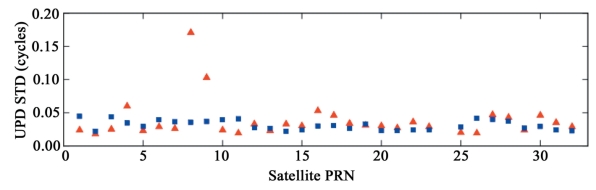
图4-10　卫星端NLUPD标准差STD

由于卫星G08和G09当天均有一段时间处于地影中，因此我们列出当天所有经历了地影卫星的时间序列，如图4-11所示。G027卫星刚开始阶段缺少数据，这是因为缺少精密卫星钟差信息。可以发现，仅有Block IIA型卫星的UPD经常会发生一个大小约为0.3～0.4周的跳变。这很可能是由卫星出地影后的偏航姿态模型不精确、地影中力学模型不精确而引起的。当移除这种跳变后，卫星G08和G09 UPD的标准差分别减小为0.03，0.04周，这与其他正常卫星相当。

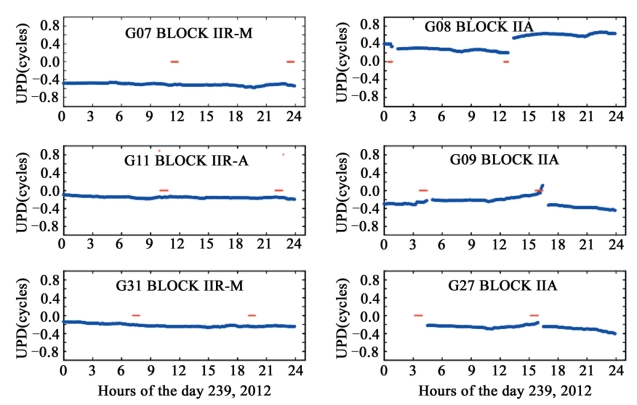
图4-11　处于日食的各卫星的时间序列

因此，在最终的参数估计中，对于BLOCLK IIA卫星，至少在出地影后，应该额外估计一个UPD参数。

2.UPD质量评估

PPP模糊度解算中模糊度的固定率可以直接作为被估UPD参数的质量的标准，其至少代表了NLUPD与模糊度参数的一致性。尽管从以上分析中可知NLUPD参数也是相当稳定的，但是为了尽可能多固定的模糊度参数，在数据处理时我们仍然逐历元地估计UPD参数。

根据统计结果，460个测站中每天大约有300个测站的所有模糊度均可被固定，有大约130个测站的模糊度固定率在95%～100%，其他的均在90%～95%。从统计结果来看，经历地影的卫星的模糊度固定率与其他卫星相差不大，大部分没有固定的模糊度一般都与某些低高度角卫星相关。这些结果说明，估计的NLUPD与模糊度参数具有很高的一致性，这对于整网处理来说是非常重要的。(www.xing528.com)

3.测站坐标

方案A和方案B估计的参数估值几乎相同，不同的仅仅是方案A中的钟差包含了NLUPD。此处仅采用了方案B的测站坐标结果来评估测站精度。将方案B的测站坐标通过7参数平移旋转后与IGS周解结果进行比较，结果表明，E，N和U方向的平均RMS值分别优于2.3mm，2.5mm和5.9mm，这个量级与各IGS分析中心与IGS最终产品间的平均偏差相当。

4.卫星轨道

为了评估估计的卫星轨道精度，首先将其与IGS最终轨道进行比较，然后对其相邻两天间的轨道重叠偏差进行分析。

将采用传统策略对包含100个测站的核心网进行处理得到的轨道、采用方案B处理同样100个测站的核心网得到的轨道，以及采用方案B对所有460个测站的网进行处理得到的轨道，分别与IGS最终轨道产品进行比较。图4-12表示的是这三种轨道，从年积日201天到289天的相对于IGS最终轨道的平均RMS值，其中红色表示采用传统策略对包含100个测站点的核心站网进行处理得到的轨道相对IGS最终轨道的平均RMS值；绿色表示采用方案B对同样100个测站的核心站网进行处理得到的轨道相对IGS最终轨道的平均RMS值；蓝色表示采用新策略对包含所有460个测站点的核心站网进行处理得到的轨道相对于IGS最终轨道的平均RMS值。

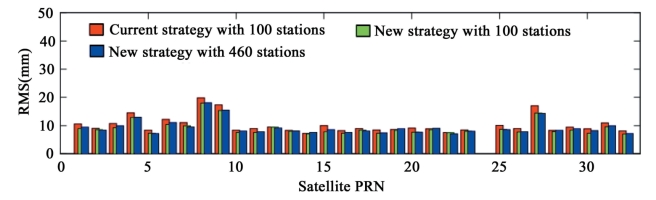
图4-12　卫星轨道RMS值

从图4-12中可以发现，除了进入地影的Block IIA型卫星(如G04，G08，G09和G027)外，其余大部分卫星轨道的RMS值均小于10mm。通过比较图中红色和绿色的部分，可以发现采用同样的约100个测站，采用方案B(新策略)可以将RMS值从10.2mm减少到9.0mm。然而，当利用方案B(新策略)处理所有460个测站时，所得到的轨道相对于IGS最终轨道平均RMS值为9.2mm，略大于100个核心站网的结果，这可能意味着IGS最终产品并不一定适合轨道精度高低的准则。相邻天之间重叠轨道偏差RMS值可以作为轨道内符合的一个更加可靠的标准。与前面类似，将采用传统策略对包含100个测站的核心网进行处理得到的轨道、采用方案B处理同样100个测站的核心网得到的轨道，以及采用方案B对所有460个测站的网进行处理得到的轨道，分别进行相邻天之间重叠轨道偏差的RMS进行统计，统计时间段仍为2012年201天到289天。其结果分别如图4-13中的红色、绿色和蓝色所示。可以发现处理同样100个测站的数据，采用方案B的结果明显优于采用传统策略的结果，尤其是那些在传统策略结果中较差的卫星，其RMS减少显著，如G06、G09、G15和G27卫星的提高幅度分别为19%、15%、14%和26%。总体来说，所有卫星的平均重叠轨道RMS值减小了约9.8%，从27.6mm减小为24.8mm。其主要原因是直接固定非差模糊度较固定双差模糊度具有更好的数据的连续性。由于卫星运动的周期性，在固定双差模糊度的策略中，每个站星对一天内包含的模糊度往往大于1，而在Carrier-range中，每个站星对仅有1个模糊度参数。

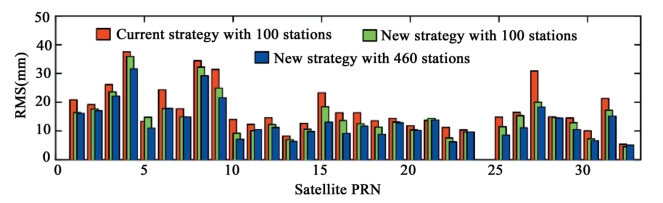
图4-13　卫星重复轨道RMS值

此外，当采用Carrier-range处理了所有460个测站时，其重叠轨道RMS值将进一步减小为23.2mm。

5.计算效率

为了测试新策略的运行效率，实验分别采用方案A、方案B、方案C处理包含不同测站数目的GPS网，比较分析其计算时间，所有的测试均在一台系统为MAC OS的电脑上进行，其CPU为Intel Core i7 2.6GHz，内存为16G。在GNSS数据处理过程中，残差迭代编辑占据了大部分数据处理时间。一般而言，基于验后残差的编辑有三种模式：网模式(如GAMIT软件)、基线模式(如Bernese软件)和单站模式(如EPOS和PANDA软件)。基于网模式的残差编辑效率最低，尤其是当存在少数数据质量差的测站时，其迭代次数将显著增加，而单站数据清理相对而言则具有实现简单，计算效率高的特点。因此，为了提高效率，PPP技术被用来进行单站数据清理，如IGS TIGA工程数据处理等。在Carrierrange策略中，同样可以认为是通过PPP来进行数据清理，相对网解而言，额外的步骤为UPD估计、PPP模糊度固定以及新RINEX产生三个步骤。UPD估计对于24d解数据仅需要约1min，而对于一个采样间隔为30s的数据，其他步骤仅需5s，更重要的是，这是基于单站处理的，即可以使用多台计算机同时并行处理。因此实验在比较计算的时间的时候，仅仅比较了单次参数估计过程的时间。

从图4-14可知，方案B需要的计算时间略长于方案A，这是因为方案B中待估参数略多(对每个测站和每颗卫星多估计了一个UPD参数)。方案A和B随着测站数目的增加，所需的计算时间几乎呈线性增长。而方案C所需时间几乎呈指数趋势增长。当处理约460个测站时，方案A、方案B和方案C分别需要的时间长约为14min、16min和82min。也就是说，相对于仅保留活跃参数的参数消去法，新解算策略可以节省6/7的时间。

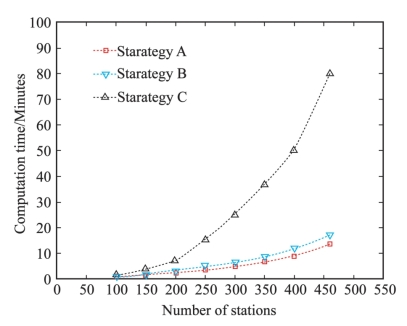
图4-14　运行效率统计图