选择最大无关双差模糊度映射算子d的应用

根据葛茂荣(Ge，et al.，2005)等人于2005年提出的基于“最大可能性”原则的独立模糊度选取方法，模糊度选取过程分为如下两步：

(1)基线范围

本方法中，大规模GNSS基准站网中所有基线均需进行搜索。在任一基线上，首先由载波相位及伪距组合观测值计算其宽巷模糊度(Melbourne，1985；魏子卿等，1998)，并计算其可固定至最接近的整数的概率P0如下(Blewitt，1989；Dong，et al.，1989)：

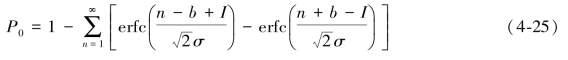
其中

式中，b、σ分别为宽巷模糊度的估值、中误差，I为b的最近整数。

置信水平通常可取α＝0.1%(Dong，et al.，1989)，亦即，若P0＞1-α，则该宽巷模糊度可以固定至与其最接近的整数，反之则暂未固定。由前所述可知，固定宽巷模糊度是LC双差模糊度可固定的前提，只有宽巷模糊度固定，对应的LC双差模糊度才可固定。

对应LC双差模糊度的估值及其方差可由组成双差模糊度的四个非差模糊度浮点解及其方差得到，其形式为：

式中，bc为组成双差模糊度的四个非差模糊度向量，Cbc为其方差矩阵，D为组成双差模糊度的映射矩阵。

在宽巷模糊度固定后，相应的窄巷模糊度估值及其方差可由下式得到：

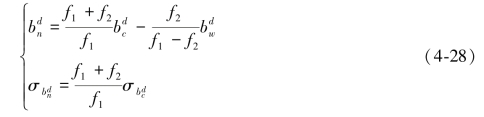
窄巷模糊度的固定概率与宽巷模糊度的计算方式一致。LC双差模糊度的固定是一个迭代的过程，当部分LC双差模糊度固定后，窄巷模糊度的估值与方差会更新，从而其固定概率也会更新。(www.xing528.com)

由上述过程，可以将单条基线上所有双差模糊度进行排序。其宽、窄巷模糊度均可固定的LC双差模糊度子集应排在最前，其次仅为宽巷模糊度可固定的LC双差模糊度子集。在每个子集内部，LC双差模糊度按宽、窄巷模糊度固定概率的乘积以降序排列。由于在模糊度固定过程中要求映射矩阵可逆，因此应将所有其他未能固定的模糊度放置在基线双差模糊度排序的最后部分。在排序完成后，可按照Gram-Schmidt法则进行模糊度参数的独立性检验，从而得到单条基线上的全部独立双差模糊度。

(2)全网范围

在全网所有基线均按照步骤(1)得到单条基线上的独立双差模糊度参数后，对所有选出的候选独立双差模糊度参数按照Gram-Schmidt法则进行独立性检验，从而获得整网的全部独立双差模糊度参数。

基于“最大可能性”原则的独立双差模糊度选取方法在具体实现时，其算法流程如图4-7所示。

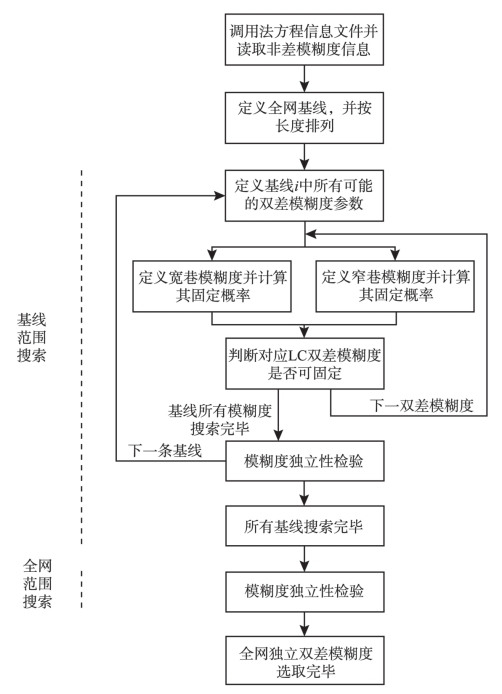
图4-7　基于“最大可能性”原则的模糊度选取方法流程图

本方法在编程实现时，有两个具体问题需要考虑：

①理论上说，本方法中所有基线均需进行独立模糊度的搜索。但在实际算法实现中，过长的基线并不需包含在内。例如，对于一个80～100站的全球网来说，考虑超过4000km的基线，所得到的独立模糊度参数仅比只考虑4000km以下基线时多2%～3%，但计算时间会大大增加(Ge，et al.，2005)。因此，在处理实际数据时，可以仅考虑4000km以下的基线。

②在任一基线上，所有可形成的双差模糊度均视为待选模糊度参数。但根据实际数据处理经验，连续观测时间小于10min的双差模糊度通常难以固定，因此在实际搜索时可只考虑观测弧段超过10min的双差模糊度作为待选参数。

由上文可知，基于“最大可能性”原则的独立双差模糊度选取方法是根据各个LC双差模糊度的固定概率来进行选取的，相对已有方法，其优点可以概括如下(Ge，et al.，2005)：

①不可固定的模糊度参数在候选模糊度排列中不会优于可固定的模糊度参数，从而保证了模糊度固定的成功率；

②由于宽、窄巷模糊度固定概率仅由载波相位及伪距组合观测值计算得来，因此体现了真实的伪距观测值质量；

③选取的独立双差模糊度是从所有双差模糊度中得来的，因此最大限度地避免了模糊度丢失的问题；

④将搜索过程划分为基线、全网范围两步进行，大大提升了计算效率。