GNSS基准站网数据处理方法：参数消去-恢复法简化且精确

为了验证参数消去-恢复法在大规模GNSS基准站网数据处理中应用的效果，本节通过解算时间、所用计算机内存、解算结果等一系列指标来对参数消去-恢复法进行分析。

1.解算时间比较

解算时间是评判参数消去-恢复法效果的关键指标之一，也是实现大规模GNSS基准站网高性能数据处理的关键之一。

为了评判参数消去-恢复方法在大规模GNSS基准站网高性能数据处理中所用解算时间，本节使用2009年5月2日(年积日122天)的全球IGS连续运行跟踪站数据(采样间隔为300s)，在30～250个测站情况下的解算时间加以对比，不同情况下测站分布如图4-2所示，解算时间如图4-3所示。策略A为不采用参数消去-恢复法，策略B为采用参数消去-恢复法。为了加快计算速度，法方程解算采用基于OPENMP并行计算的乔里斯基分解法，并行线程为4。

由图4-3可知，当测站数目小于50站时，是否使用参数消去-恢复法，解算时间相差并不大，但随着测站数目增多，策略A所用解算时间快速增加，测站数目超过200个后解算时间已经超过7小时；而策略B解算时间随测站数目的增多大致呈线性增长趋势，且250个测站所用解算时间也未超过3h。由此可见，使用参数消去-恢复法可以大幅提升最小二乘估计的解算速度，从而达到大规模GNSS基准站网的高性能数据处理目的。同时，需要注意的是，在完整的GNSS精密数据处理中，至少需要进行两次最小二乘估计解算(分别得到浮点解和固定解)，因此，采用参数消去-恢复法所节省的解算时间会更为可观。

图4-2　不同情况下测站分布图

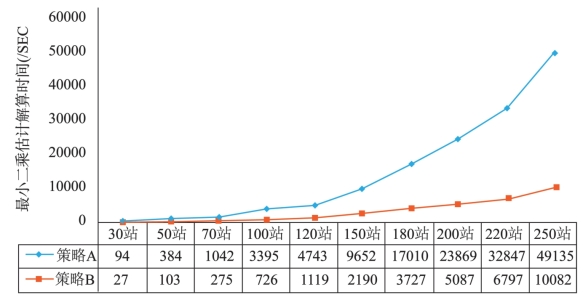
图4-3　不同测站情况下解算时间对比图(单位：s)

2.所用计算机内存比较

解算所用计算机内存是实现大规模GNSS基准站网高性能数据处理的关键指标之一，为了能够同时解算更多测站的数据，必须要求相同测站数量情况下所用计算机内存尽可能少。

由于所用计算机内存直接与法方程维数相关，因此，此处使用2009年5月2日(年积日122天)的全球IGS连续运行跟踪站数据(采样间隔为300s)，将不同测站数目情况下不同策略法方程维数以及所用计算机内存两个指标加以对比。法方程实际维数对比如图4-4所示，所用计算机内存对比如图4-5所示。策略A为不采用参数消去-恢复法，策略B为采用参数消去-恢复法。

(www.xing528.com)

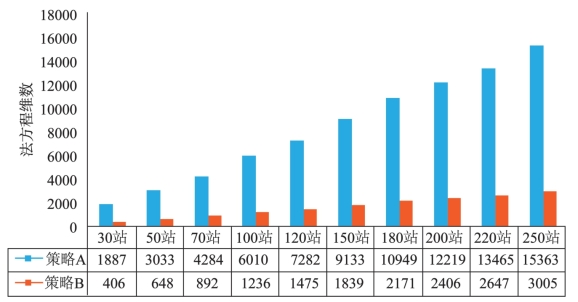
图4-4　不同测站情况下法方程维数对比图

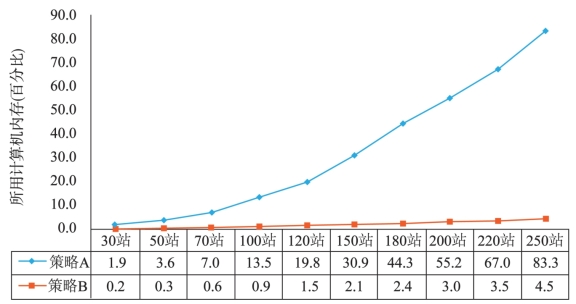
图4-5　不同测站情况下所用内存对比图

由图4-4可以看到，使用参数消去-恢复法后，法方程维数大幅度减小，250站时策略B法方程维数仅为3005，约为策略A的20%；同时，由图4-5可知，在使用参数消去-恢复法后，解算时所用计算机内存同样大幅度降低，250站情况下所用内存仅为184MB。因此，可以认为，在使用了本节所述的参数消去-恢复法后，能够在个人计算机平台上处理大规模GNSS基准站网的观测数据。同时，解算时所用的计算机内存资源大幅度降低，在非极端情况下可以不予考虑解算时内存溢出问题。

3.解算结果比较

为了验证参数消去-恢复法解算的精度，选择2009年5月2日(年积日122天)350站的全球IGS连续运行跟踪站数据(采样间隔300s)，测站分布如图4-6所示。

首先采用参数消去-恢复法加以处理，并与未采用参数消去-恢复法的结果加以比较，见表4-2。

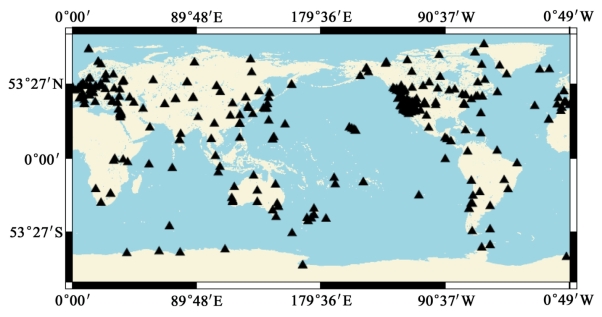
图4-6　全球IGS跟踪站分布图(350站)

表4-2　参数消去-恢复法使用与否结果比较(单位：mm)

由表4-2可知，使用参数消去-恢复法，在大幅度提升解算效率的同时，解算结果与未使用参数消去-恢复法时基本一致，二者解算的较差最大不超过0.1mm。

因此，可以认为，基于参数消去-恢复法的最小二乘估计不仅可以大幅度提高解算效率，降低解算时所需的计算机内存，同时也保证了定位精度，是实现大规模GNSS基准站网高性能数据处理的一个行之有效的方法。