最小二乘模糊度降相关平差法(LAMBDA)

在模糊度固定过程中，对于一个模糊度参数，假设落入其置信区间内的整数个数为n个，则称这n个整数为此模糊度参数的备选解。所有模糊度参数的备选解构成了整个模糊度向量N的备选组，而正确的模糊度组合仅仅是其中的一组。理论上而言，使观测值的残差平方和最小的一组模糊度即为正确的模糊度组合，即使一个模糊度参数固定错误也会导致较大的残差。在解算过程中，如果模糊度参数的实数解精度很低，参数之间的相关性较强，则模糊度参数的备选组合数量是惊人的，求取每个备选组合所对应的残差平方和需要耗费巨大的工作量。

最小二乘模糊度降相关平差法(Least-square AMBiguity Decorrelation Adjustment)，简称LAMBDA方法，是由Teunissen教授于1993年提出的。该方法通过整数变换以减小搜索范围，是目前比较有效的一种模糊度搜索方法。

通过从备选组中挑选模糊度组合使观测值的残差平方和最小等价于：

式中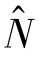，为实数模糊度解，N为所求的模糊度整数解，为实数模糊度解的协因数阵。LAMBDA方法不直接对模糊度参数进行搜索，而是先对模糊度实数解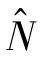及其协方差阵进行整数变换：

式中，Z为整数变换矩阵。整数变换具有以下性质：当N为整数时，变换后所得z也为整数，反之亦然。经过变换之后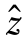，之间的相关性大幅降低，而且方差也减小，此时式(4-1)等价于：(www.xing528.com)

再利用前面所述算法求得z的置信空间，构成z值的备选组合，然后逐一搜索挑选出满足上式的整数z值组合。通过前述的整数变换使z值之间的相关性大幅降低，故此时的搜索将相当迅速。

求得满足上式的z值组合后再实施逆变换：

此处的整数N值即为我们最初所寻求的整周模糊度整数解组合(李征航等，2010)。